2024年7月号
特集
行列式に始まる表現論と組合せ論
- α-行列式
- リース行列式
- 表現の既約分解
確率分布の統一的扱いの考察から現れた ![]() 行列式は行列式とパーマネントを補間するものです。それ自体に不変性はありませんが、それが生成する一般線型(リー)群の表現は、その既約分解を通して興味深い不変式を定め、対称関数、表現論、組合せ論、数論、確率論などの未解決予想にもつながる豊かな数学を生んでいます。
行列式は行列式とパーマネントを補間するものです。それ自体に不変性はありませんが、それが生成する一般線型(リー)群の表現は、その既約分解を通して興味深い不変式を定め、対称関数、表現論、組合せ論、数論、確率論などの未解決予想にもつながる豊かな数学を生んでいます。
Cid Reyes-Bustos/若山 正人(わかやま まさと)
NTT基礎数学研究センタ
はじめに
本稿では、リー群の中でも行列の線型変換としての合成で積が定義されている行列のなす群、中でももっとも基本的な一般線型群の表現論の、またその特別な表現論を出発点として、さまざまな数学につながり広がる研究を、未解決予想や探究すべき重要テーマに寄り道をしつつ紹介します。なおリー群とは、群構造を持つ幾何学的対象(微分可能多様体)であり、群構造と可微分構造とが両立しているものです。
■群
集合 ![]() が群であるとは、①積
が群であるとは、①積 ![]() が定義されて結合律
が定義されて結合律 ![]() が成立、②単位元
が成立、②単位元 ![]() が存在:すべての
が存在:すべての ![]() に対して
に対して ![]() が成立、③逆元
が成立、③逆元 ![]() がつねに存在する:
がつねに存在する: ![]() =
= ![]() =
= ![]() が成立。
が成立。
例としては、 ![]() 個の文字の置換の全体からなる
個の文字の置換の全体からなる ![]() 次対称群
次対称群 ![]() 、そして
、そして ![]() 次の実数(複素数)を成分に持つ正則行列(逆行列を持つ行列)全体がなす一般線型群
次の実数(複素数)を成分に持つ正則行列(逆行列を持つ行列)全体がなす一般線型群 ![]() などがあります。後者は本稿で扱う群です。
などがあります。後者は本稿で扱う群です。
■リー群・リー環の表現論
![]() の表現とは
の表現とは ![]() からベクトル空間
からベクトル空間 ![]() の線型変換のなす群への準同型(
の線型変換のなす群への準同型( ![]() 積を保つ)写像
積を保つ)写像 ![]() の組 (
の組 ( ![]() ,
, ![]() ) です。ここではもっぱら有限次元表現のみを考えます。
) です。ここではもっぱら有限次元表現のみを考えます。![]() が無限次元のときは、位相を入れて考える必要があります。
が無限次元のときは、位相を入れて考える必要があります。 ![]() として、通常は複素ベクトル空間を考えます。(
として、通常は複素ベクトル空間を考えます。( ![]() 次元の)
次元の)![]() に内積(エルミート内積)を入れて、ユニタリ行列がなすユニタリ群
に内積(エルミート内積)を入れて、ユニタリ行列がなすユニタリ群 ![]() (
( ![]() ) を考えることもあります。また、この状況を、群
) を考えることもあります。また、この状況を、群 ![]() が
が ![]() に作用している、あるいは
に作用している、あるいは ![]() は
は ![]() 加群であると言ったりします。さらに、文脈上明白であれば記号
加群であると言ったりします。さらに、文脈上明白であれば記号 ![]() を省略します。表現論は、量子力学や相対論という革命的な物理理論と並走するように発展したため、用語において数学と物理のニュアンスが混在していることが多くあり、利点とともに戸惑いを生むこともあります。
を省略します。表現論は、量子力学や相対論という革命的な物理理論と並走するように発展したため、用語において数学と物理のニュアンスが混在していることが多くあり、利点とともに戸惑いを生むこともあります。
しかしながら、リー群 ![]() は多様体ですので、“曲がっていたり”、連結でないなど、構造が複雑であり線型代数だけでは話が徹底しません。そのため、リー群
は多様体ですので、“曲がっていたり”、連結でないなど、構造が複雑であり線型代数だけでは話が徹底しません。そのため、リー群 ![]() を“微分した”リー環
を“微分した”リー環 ![]() というものを可能な範囲で活用します。理論的には道具として不足ですが、本稿では有限次元表現のみを扱うためリー環で事が足ります。実際、幾何学的にはリー環とは単位元
というものを可能な範囲で活用します。理論的には道具として不足ですが、本稿では有限次元表現のみを扱うためリー環で事が足ります。実際、幾何学的にはリー環とは単位元 ![]() における接空間がなす線形空間です。よって線形代数を駆使できます。つまり、リー群の作用からくる変換の無限小変換を考えるわけです。
における接空間がなす線形空間です。よって線形代数を駆使できます。つまり、リー群の作用からくる変換の無限小変換を考えるわけです。![]() のリー環
のリー環 ![]() は
は ![]() 次行列全体(全行列環)です。そこで
次行列全体(全行列環)です。そこで ![]() ∈
∈ ![]() に対して行列の指数写像を考えるとdet (exp
に対して行列の指数写像を考えるとdet (exp ![]() ) =
) = ![]() ≠0からexp
≠0からexp ![]() ∈
∈ ![]() が分かります。したがって、
が分かります。したがって、 ![]() が
が ![]() 上の多項式
上の多項式 ![]() に(
に( ![]() ,
, ![]() )(
)( ![]() ) =
) = ![]() として作用するとき、その無限小作用は次のように定まります。
として作用するとき、その無限小作用は次のように定まります。
![]()
■ α- 行列式の表現論研究の契機
確率論の文脈で定義された ![]() 行列式は行列式の拡張であり、行列式とパーマネント(行列式の定義において符号がないもの)を補間するものです。以下で採用する
行列式は行列式の拡張であり、行列式とパーマネント(行列式の定義において符号がないもの)を補間するものです。以下で採用する ![]() 行列式の定義によると、それは
行列式の定義によると、それは ![]() = −1のときに通常の行列式となり、
= −1のときに通常の行列式となり、![]() = 1のときにパーマネントとなります。
= 1のときにパーマネントとなります。![]() 行列式という名称は白井・高橋(1)に沿ったものです(
行列式という名称は白井・高橋(1)に沿ったものです( ![]() 行列式は(2)において、最初は
行列式は(2)において、最初は ![]() パーマネントとして導入されました)。そこでは、昨今の金融時系列データ解析などで重要な、ボゾン点過程、ポアソン点過程、フェルミオン点過程の一般化となる点過程の構成を目的に
パーマネントとして導入されました)。そこでは、昨今の金融時系列データ解析などで重要な、ボゾン点過程、ポアソン点過程、フェルミオン点過程の一般化となる点過程の構成を目的に ![]() 行列式を用いました。しかしながら、
行列式を用いました。しかしながら、 ![]() 行列式(
行列式( ![]() ≠ −1) はdet(
≠ −1) はdet( ![]() ) = det(
) = det( ![]() ) det(
) det( ![]() ) のような乗法性を持ちません。それでは
) のような乗法性を持ちません。それでは
疑問1:積の性質(乗法性)はいったいどこに行ってしまったのでしょう?
行列式は ![]() の1次元表現を定めます。パーマネントが定めるのは1次元表現ではありませんが、対称テンソル積が張る空間上に既約表現を定めます。ここで既約表現とは、{0}と自分自身
の1次元表現を定めます。パーマネントが定めるのは1次元表現ではありませんが、対称テンソル積が張る空間上に既約表現を定めます。ここで既約表現とは、{0}と自分自身 ![]() 以外に群
以外に群 ![]() の作用で不変な部分空間がない表現のことを言います。気分としては、(1と自分自身以外に約数がない)素数や素粒子のようなものです。では
の作用で不変な部分空間がない表現のことを言います。気分としては、(1と自分自身以外に約数がない)素数や素粒子のようなものです。では
疑問2:一般の ![]() の場合、群で動かすとどんな空間を張るのでしょう?
の場合、群で動かすとどんな空間を張るのでしょう?
以上は ![]() 行列式が定める
行列式が定める ![]() の表現論を考える契機となった疑問です(3)。
の表現論を考える契機となった疑問です(3)。
α- 行列式
![]() 行列式はパラメータ
行列式はパラメータ ![]() による行列式の変形であり、正方行列
による行列式の変形であり、正方行列 ![]() =
= ![]() に対して式(1)のように定義されます。ここで
に対して式(1)のように定義されます。ここで ![]() は
は ![]() のサイクル分解に現れるサイクルの個数です。以下では
のサイクル分解に現れるサイクルの個数です。以下では ![]() (
( ![]() ) : =
) : = ![]() −
− ![]() とおきます。
とおきます。 ![]() (
( ![]() ) は
) は ![]() を互換の積として表す際に必要となる互換の個数の最小値にも等しいことに注意しておきます。
を互換の積として表す際に必要となる互換の個数の最小値にも等しいことに注意しておきます。
Vere-Jonesの定理(2)は、![]() の展開が次のように
の展開が次のように ![]() 行列式を使って書けるというものです(式(2))。この等式の発見の経緯と応用については 参考文献(4)を参照ください。
行列式を使って書けるというものです(式(2))。この等式の発見の経緯と応用については 参考文献(4)を参照ください。
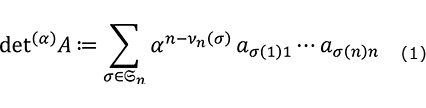
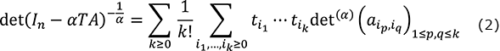
■表現論の準備
![]() とそのリー環
とそのリー環 ![]() の有限次元既約表現(既約
の有限次元既約表現(既約 ![]() - 加群)は、最高ウェイトというものでパラメトライズされることが知られています。その背後には、
- 加群)は、最高ウェイトというものでパラメトライズされることが知られています。その背後には、![]() の
の ![]() への標準的な作用に対して、
への標準的な作用に対して、![]() 個のテンソル積空間
個のテンソル積空間 ![]() に対する自然な
に対する自然な ![]() の作用を考えると、
の作用を考えると、![]() 個のテンソル積の間の置換として働く対称群
個のテンソル積の間の置換として働く対称群 ![]() の作用が(互いに精一杯に)交換可能という事実から導かれる双対性があるからです。これが有名な Schur-Weyl 相互律です(5)。また、最高ウェイトは分割というものと同一視できます。ただし
の作用が(互いに精一杯に)交換可能という事実から導かれる双対性があるからです。これが有名な Schur-Weyl 相互律です(5)。また、最高ウェイトは分割というものと同一視できます。ただし ![]() が
が ![]() の分割とは
の分割とは ![]() =
= ![]() といい、このとき
といい、このとき ![]() ⊢
⊢ ![]() と表します。
と表します。![]() (
( ![]() ) で
) で ![]() の長さ(非ゼロ成分の個数)とします。分割
の長さ(非ゼロ成分の個数)とします。分割 ![]() とそれが定めるヤング図形
とそれが定めるヤング図形
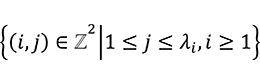
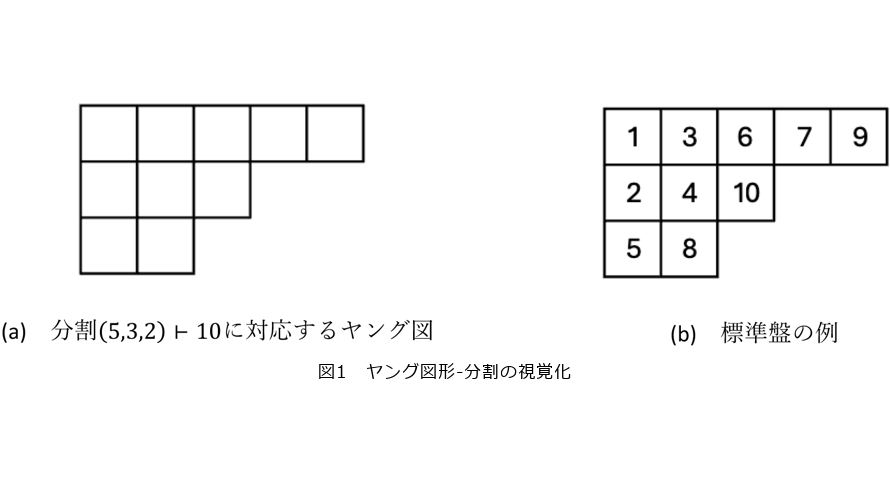
をしばしば同一視します。またヤング図形を「左揃えで、上から ![]() 段目に
段目に ![]() 個の箱を並べたもの」と図示します(図1)。Stab(
個の箱を並べたもの」と図示します(図1)。Stab( ![]() ) で
) で ![]() のヤング図形に対する標準盤の全体がなす集合を表します。ここで標準盤とは
のヤング図形に対する標準盤の全体がなす集合を表します。ここで標準盤とは ![]() 個の箱に 1,2,… ,
個の箱に 1,2,… , ![]() の数を「各行で数は左から右に増加、各列で数は上から下に増加するように入れた」ものです。
の数を「各行で数は左から右に増加、各列で数は上から下に増加するように入れた」ものです。
α- 行列式が生成する巡回加群
一般線型リー代数 ![]() の
の ![]() に関する多項式(がなす)環
に関する多項式(がなす)環 ![]() への作用は合成関数の微分法より
への作用は合成関数の微分法より
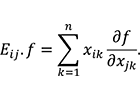
ただし ![]() (1 ≤
(1 ≤ ![]() 、
、![]() ≤
≤ ![]() ) は
) は ![]() の標準基底(行列単位)です。
の標準基底(行列単位)です。![]() =
= ![]() として、
として、![]() が生成する巡回
が生成する巡回 ![]() -加群を
-加群を ![]() とします。つまり
とします。つまり ![]() は、
は、![]() ∈
∈ ![]() に
に ![]() のあらゆる元を任意回作用させて、そのすべてで張られるベクトル空間(加群)です。
のあらゆる元を任意回作用させて、そのすべてで張られるベクトル空間(加群)です。![]() = −1のときは
= −1のときは ![]() = det
= det ![]() なので
なので ![]() =
= ![]() ⋅det
⋅det ![]() です。したがって、
です。したがって、![]() の構造を調べるという問題は疑問1と疑問2双方への回答をめざすものです。
の構造を調べるという問題は疑問1と疑問2双方への回答をめざすものです。
定理 2.1 (3)。![]() を最高ウェイト
を最高ウェイト ![]() を持つ既約
を持つ既約 ![]() -加群とする。このとき
-加群とする。このとき ![]() は次のように既約分解される:
は次のように既約分解される:
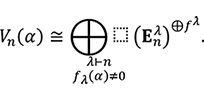
ただし ![]() : = |Stab(
: = |Stab( ![]() )|(元の個数)、
)|(元の個数)、![]() : =
: = ![]() (1+ (
(1+ ( ![]() −
− ![]() )
) ![]() )(分割
)(分割 ![]() の content polynomial)である。
の content polynomial)である。
この定理は、![]() ∉
∉ ![]() であれば、
であれば、![]() は標準表現
は標準表現 ![]() のテンソル積
のテンソル積 ![]() に同値であり、
に同値であり、![]() が|
が| ![]() |未満の整数の逆数となる場合に構造の退化が起こる、という状況を示しています。
|未満の整数の逆数となる場合に構造の退化が起こる、という状況を示しています。
この問題の自然な一般化として、冪 ![]() が生成する巡回
が生成する巡回 ![]() - 加群の構造を調べる問題があります。この場合、既約分解に現れる各最高ウェイト加群に、組合せ論的に非自明な重複度の評価が現れます。この重複度の評価は一般的に困難です。ただし
- 加群の構造を調べる問題があります。この場合、既約分解に現れる各最高ウェイト加群に、組合せ論的に非自明な重複度の評価が現れます。この重複度の評価は一般的に困難です。ただし ![]() = 2 のときは、対称群とそのヤング部分群の対
= 2 のときは、対称群とそのヤング部分群の対 ![]() がゲルファント対と呼ばれるものとなり、ゲルファント対に対する帯球関数の値が超幾何多項式を用いて書けるという事実から、重複度を明示的に表す公式が得られます(6)。一般の場合は具体的な予想すらできていませんが興味が尽きない問題です。また、対称関数の理論においてもっとも古典的で根本的な問題の1つにプレシズム(7)といわれるものがあります。参考文献(8)では
がゲルファント対と呼ばれるものとなり、ゲルファント対に対する帯球関数の値が超幾何多項式を用いて書けるという事実から、重複度を明示的に表す公式が得られます(6)。一般の場合は具体的な予想すらできていませんが興味が尽きない問題です。また、対称関数の理論においてもっとも古典的で根本的な問題の1つにプレシズム(7)といわれるものがあります。参考文献(8)では ![]() (パーマネント)の冪に関してそれが生成する巡回加群の構造からプレシズムについて対称テンソル積に関するある予想を提示していますが、高次の冪
(パーマネント)の冪に関してそれが生成する巡回加群の構造からプレシズムについて対称テンソル積に関するある予想を提示していますが、高次の冪 ![]() の場合は大変難しく、
の場合は大変難しく、![]() = 2では任意の
= 2では任意の ![]() に対して確認できるものの、
に対して確認できるものの、![]() = 3 のときでさえ
= 3 のときでさえ ![]() = 2 の場合しか確認できていません。また対応する研究は量子群の場合にも進められています(9)。特に
= 2 の場合しか確認できていません。また対応する研究は量子群の場合にも進められています(9)。特に ![]() = 2 の場合に、上述の重複度が
= 2 の場合に、上述の重複度が ![]() - 超幾何多項式と超幾何多項式の両者! が混ざり合った多項式で表示され、ふしぎな魅力を感じます(10)(11)。
- 超幾何多項式と超幾何多項式の両者! が混ざり合った多項式で表示され、ふしぎな魅力を感じます(10)(11)。
リース行列式
![]() が
が ![]() のときに
のときに ![]() 行列式が生成する巡回加群は退化するのでした。この特殊性を注意深く眺めると、
行列式が生成する巡回加群は退化するのでした。この特殊性を注意深く眺めると、![]() =
= ![]() のとき
のとき ![]() 行列式に弱い交代性が見つかります。実際、1, 2, …,
行列式に弱い交代性が見つかります。実際、1, 2, …, ![]() から任意に
から任意に ![]() + 1 文字を選び、他を動かさない置換全体からなる
+ 1 文字を選び、他を動かさない置換全体からなる ![]() の部分群を
の部分群を ![]() とすると
とすると ![]() は、( 1 +
は、( 1 + ![]() )( 1 + 2
)( 1 + 2![]() ) … ( 1 +
) … ( 1 + ![]()
![]() )(
)( ![]() ∈
∈ ![]() ) を因数に持ちます。つまり
) を因数に持ちます。つまり ![]() = 0 となり
= 0 となり ![]() の列のうち
の列のうち ![]() +1個が一致すれば
+1個が一致すれば ![]()
![]() = 0 が分かります。また
= 0 が分かります。また ![]() を
を![]() ∈
∈ ![]() に対する置換行列とすると
に対する置換行列とすると ![]() =
= ![]() により、行についても同様です。この弱い交代性のおかげでヴァンデルモンド行列式やコーシー行列式といった特殊行列式の類似も得られます(12)。
により、行についても同様です。この弱い交代性のおかげでヴァンデルモンド行列式やコーシー行列式といった特殊行列式の類似も得られます(12)。
■リース行列式と不変式
すべての成分が1である ![]() ×
× ![]() 行列を
行列を ![]() とします。
とします。 ![]() に対してその
に対してその ![]() - リース行列式を以下で定義します。
- リース行列式を以下で定義します。
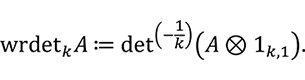
例えば、リース行列式(式(3))は、以下のように行列式と類似の特徴付けを持つ左 -![]() ,右 -
,右 -![]() ≀
≀![]() 相対不変式です。ここで
相対不変式です。ここで ![]() ≀
≀![]() は
は ![]() と
と ![]() のリース積と呼ばれ、(2つの群から新しい群をつくる)群の半直積という概念を通して構成されるものです。
のリース積と呼ばれ、(2つの群から新しい群をつくる)群の半直積という概念を通して構成されるものです。
定理 3.1(12)。 写像 ![]() :
: ![]() →
→ ![]() であって以下を満たすものは定数倍を除いて
であって以下を満たすものは定数倍を除いて![]() ↦
↦ ![]() に限る。
に限る。
1. ![]() は列に関して多重線型写像、
は列に関して多重線型写像、
2. 任意の ![]() ∈
∈ ![]() に対して
に対して ![]() (
( ![]()
![]() ) =
) = ![]() 。特に左 -
。特に左 -![]() - 相対不変、
- 相対不変、
3. 任意の ![]() ∈
∈ ![]() ≀
≀![]() に対して
に対して ![]() = ±
= ± ![]() (
( ![]() )。特に
)。特に ![]() ∈
∈ ![]() に対して
に対して ![]() =
= ![]() (
( ![]() )。
)。
この定理の背後には ![]() -dualityという双対性があり、それを用いれば簡潔に導かれますが、(記号を適切に準備すれば)初等的かつ直接的にも証明できます。
-dualityという双対性があり、それを用いれば簡潔に導かれますが、(記号を適切に準備すれば)初等的かつ直接的にも証明できます。
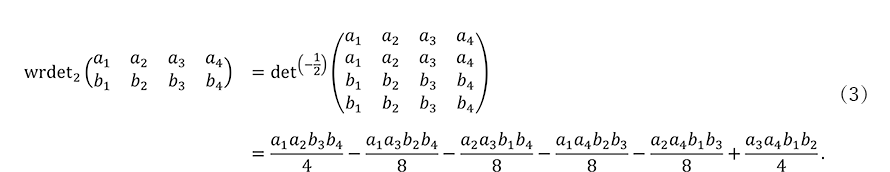
■リース行列式が定める群・部分群の群行列式アナログ
有限群の指標理論はフロベニウスによって始まりました。そのときに群行列式が重要な役割を果たしました。群行列式は、有限群 ![]() に対し、不定元
に対し、不定元 ![]() (
(![]() ∈
∈ ![]() ) を用意して
) を用意して
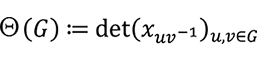
と定義されます。群行列式は群の同型類に関する完全不変量です。すなわち、次が成立します。
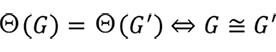
フロベニウスは自身が基本定理と呼んだ重要な定理、現代的にいうと群の正則表現( ![]() が
が ![]() 自体の群環に作用)の既約分解を与えました。このフロベニウスの成果は1896年にデデキントがフロベニウスに宛てた手紙が発端でした。デデキントは有限アーベル群に対して群行列式がどのように分解するのかを示したうえで、非アーベル群のときには群行列式がどのように分解されるかをフロベニウスに手紙で尋ねたのでした。表現論が創始された瞬間です。
自体の群環に作用)の既約分解を与えました。このフロベニウスの成果は1896年にデデキントがフロベニウスに宛てた手紙が発端でした。デデキントは有限アーベル群に対して群行列式がどのように分解するのかを示したうえで、非アーベル群のときには群行列式がどのように分解されるかをフロベニウスに手紙で尋ねたのでした。表現論が創始された瞬間です。
さて、![]() -リース行列式は
-リース行列式は ![]() ×
× ![]()
![]() 行列に対して定義されるので、有限群
行列に対して定義されるので、有限群 ![]() とその指数
とその指数 ![]() の部分群
の部分群 ![]() のペア(
のペア( ![]() ,
, ![]() ) に対して群行列式の類似を
) に対して群行列式の類似を
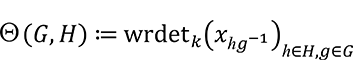
と定めたくなります。しかしながらリース行列式には列の入替に関する相対不変性がありませんので、この定義は行列成分の並び順に依存します。そのため、群の元に名前・番号を付与して定義する必要があります。今、全単射 ![]() : {0, 1, …,
: {0, 1, …, ![]()
![]() −1 } →
−1 } → ![]() を1つ固定して、
を1つ固定して、![]() と書き、これを
と書き、これを ![]() の元の番号付けと呼ぶことにします。ここで、
の元の番号付けと呼ぶことにします。ここで、![]() -代数(例えば(
-代数(例えば( ![]()
![]() −1) -変数の多項式環)
−1) -変数の多項式環)![]() を考えて
を考えて ![]() :
: ![]() →
→ ![]() を1つ定めることで特殊化と呼びます。
を1つ定めることで特殊化と呼びます。![]() が有限アーベル群のとき、
が有限アーベル群のとき、![]() の元に番号を付け、
の元に番号を付け、![]() という特殊化を選ぶと、
という特殊化を選ぶと、![]() (
( ![]() ,
, ![]() )が
)が ![]() − 1 の形の因数たちの積にきれいに分解することなどが分かります(13)。具体例を1つ挙げます。そのため、分割
− 1 の形の因数たちの積にきれいに分解することなどが分かります(13)。具体例を1つ挙げます。そのため、分割 ![]() = (
= (![]() , … ,
, … , ![]() ) ⊢
) ⊢ ![]()
![]() に対応する
に対応する ![]() の既約指標
の既約指標 ![]() を
を ![]() 上で平均して得られる両側
上で平均して得られる両側 ![]() - 不変な
- 不変な ![]() 上の関数
上の関数 ![]() を式(4)で定義しておきます。
を式(4)で定義しておきます。
例 3.1. ![]() =
= ![]() ×
× ![]() ,
, ![]() =
= ![]() × {0} のとき、式(5)で
× {0} のとき、式(5)で ![]() ,
, ![]() ∈
∈ ![]() は
は ![]() (
( ![]() ) =
) = ![]() ⊗
⊗ ![]() ,
, ![]() ⊗
⊗ ![]() = (
= ( ![]() ⊗
⊗ ![]() )
) ![]() から定まり、式(6)が得られます。特に
から定まり、式(6)が得られます。特に ![]() が3以上の奇数ならば
が3以上の奇数ならば ![]() (
( ![]() ,
, ![]() ) = 0です。
) = 0です。
しかしながら現時点では、群・部分群行列式による新しい理論は構築されていません。ただし、2つの興味深い研究が生まれました。木本によるAlon-Tarsi 予想との関連と、もう1つは群・部分群による新しいグラフの構成です。
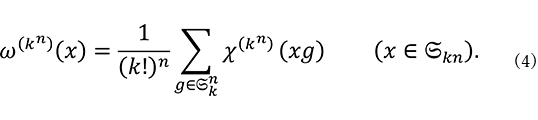
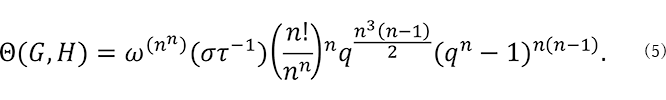

■Alon-Tarsi 予想
各行・各列の成分が 1 ∼ ![]() の順列となっている
の順列となっている ![]() 次行列を
次行列を ![]() 次のラテン方陣と呼びます。例えば3次のラテン方陣は図2〔下、右、左(実際の場所に依存します)〕にリストアップしている12個です。
次のラテン方陣と呼びます。例えば3次のラテン方陣は図2〔下、右、左(実際の場所に依存します)〕にリストアップしている12個です。![]() 次のラテン方陣
次のラテン方陣 ![]() に対してその符号sgn
に対してその符号sgn ![]() を行と列の置換の符号の積として定めます。Sgn
を行と列の置換の符号の積として定めます。Sgn ![]() = 1 のとき偶方陣、sgn
= 1 のとき偶方陣、sgn ![]() = −1 のとき奇方陣と呼びます。
= −1 のとき奇方陣と呼びます。 ![]() が奇数であれば、互換(1,2) に対して
が奇数であれば、互換(1,2) に対して ![]() =
= ![]() ですので、両者間の全単射が導かれ、
ですので、両者間の全単射が導かれ、![]() 次の偶方陣と奇方陣が同数であることは明らかです。一方で、
次の偶方陣と奇方陣が同数であることは明らかです。一方で、
予想 3.2 (Alon-Tarsi予想(1992))。![]() が偶数のとき、
が偶数のとき、![]() 次のラテン方陣において偶方陣と奇方陣の個数は異なる。
次のラテン方陣において偶方陣と奇方陣の個数は異なる。
これは、元々はグラフのある種の彩色問題に由来する予想でしたが、グラフ理論を離れたところでも、![]() 次元ベクトル空間の
次元ベクトル空間の ![]() 個の基底の合理的な選択可能性に関するRota予想や特殊ユニタリ群
個の基底の合理的な選択可能性に関するRota予想や特殊ユニタリ群 ![]() のsquare-free座標関数積のハール測度(
のsquare-free座標関数積のハール測度( ![]() -両側不変測度)による
-両側不変測度)による ![]() 全体での積分の非零性などの同値命題や、そこから従う非自明な命題もあり興味深いものです。そうした中、木本はリース行列式を用いた新しい同値命題を発見しました(12)。
全体での積分の非零性などの同値命題や、そこから従う非自明な命題もあり興味深いものです。そうした中、木本はリース行列式を用いた新しい同値命題を発見しました(12)。
定理 3.2 ![]() を偶数とする。このとき
を偶数とする。このとき ![]() 次のラテン方陣に対するAlon-Tarsi予想は以下の3つのそれぞれと同値。
次のラテン方陣に対するAlon-Tarsi予想は以下の3つのそれぞれと同値。
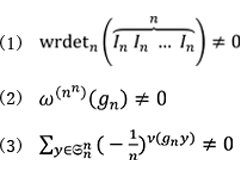
ただし ![]() ∈
∈ ![]() は
は![]() ((
(( ![]() - 1 )
- 1 ) ![]() +
+ ![]() ) =(
) =( ![]() − 1 )
− 1 ) ![]() +
+ ![]() ( 1 ≤
( 1 ≤ ![]() 、
、![]() ≤
≤ ![]() )なる置換であり、
)なる置換であり、![]() は{(
は{( ![]() − 1 )
− 1 ) ![]() +
+ ![]() | 1 ≤
| 1 ≤ ![]() ≤
≤ ![]() }(
}( ![]() = 1, … ,
= 1, … , ![]() ) たちを保つような置換の全体がなす
) たちを保つような置換の全体がなす ![]() の部分群である。
の部分群である。
容易に確かめられそうな風貌をしたAlon-Tarsi予想ですが、数論や組合せ論でしばしばみられるように手強い相手です。時点での最良成果は、![]() を奇素数として、
を奇素数として、![]() =
= ![]() + 1 の場合のDrisko(1997)、
+ 1 の場合のDrisko(1997)、![]() =
= ![]() − 1 の場合のGlynn(2010)による証明です(14)。なお、後者については、リース行列式を用いた別証明が木本(15)(16)により得られています。ところでラテン方陣の個数 ls(
− 1 の場合のGlynn(2010)による証明です(14)。なお、後者については、リース行列式を用いた別証明が木本(15)(16)により得られています。ところでラテン方陣の個数 ls( ![]() ) については、かなり弱いものですが漸近公式ls
) については、かなり弱いものですが漸近公式ls ![]() ∼
∼ ![]() が知られています(17)。偶奇方陣の個数についても漸近的には大体等しいようです(そのため、予想の解決が難しいといってもよいでしょう)。そこで新しい研究課題を挙げておきましょう。
が知られています(17)。偶奇方陣の個数についても漸近的には大体等しいようです(そのため、予想の解決が難しいといってもよいでしょう)。そこで新しい研究課題を挙げておきましょう。
問題 3.3 次の比例式が成り立つようなラテン方陣ゼータ“ ![]() ”を(あれば)見つけよ。
”を(あれば)見つけよ。
究極の素数定理(↔リーマン予想): リーマンゼータ ![]() =Alon-Tarsi予想 :
=Alon-Tarsi予想 : ![]() 。
。

■群・部分群ペアグラフ
グラフ理論においてラマヌジャングラフというものがあります。ラマヌジャングラフはスペクトルグラフ理論的に“最良の”高拡散性・急撹拌性を持つエクスパンダーグラフです。ラマヌジャングラフはその性質から、例えば暗号学的ハッシュ関数の構成といった応用を持つため重要です。またグラフがラマヌジャンであることはそのグラフのゼータ関数がリーマン予想の類似を満たすことと同値であり、数論的観点からも興味を持たれてきました。ラマヌジャングラフの無限族を具体的に構成することは重要課題の1つで、Lubotzky-Phillips-Sarnak(1994)によるハミルトン四元数環とその極大整環を用いた有限体上の射影線型群に対するケーリーグラフとしての構成や、Pizer(1990)による有限体上の超楕円曲線の同型類の間の同種写像を用いた構成が有名です。ここでケーリーグラフとは、(有限生成の)群 ![]() の各元を頂点とし、生成元をかけることによって移る元を辺でつないだグラフです。前者では、実際に
の各元を頂点とし、生成元をかけることによって移る元を辺でつないだグラフです。前者では、実際に ![]() が4を法として1と合同な素数であるときに(
が4を法として1と合同な素数であるときに( ![]() + 1 )-正則ラマヌジャングラフの無限族を構成しました。
+ 1 )-正則ラマヌジャングラフの無限族を構成しました。
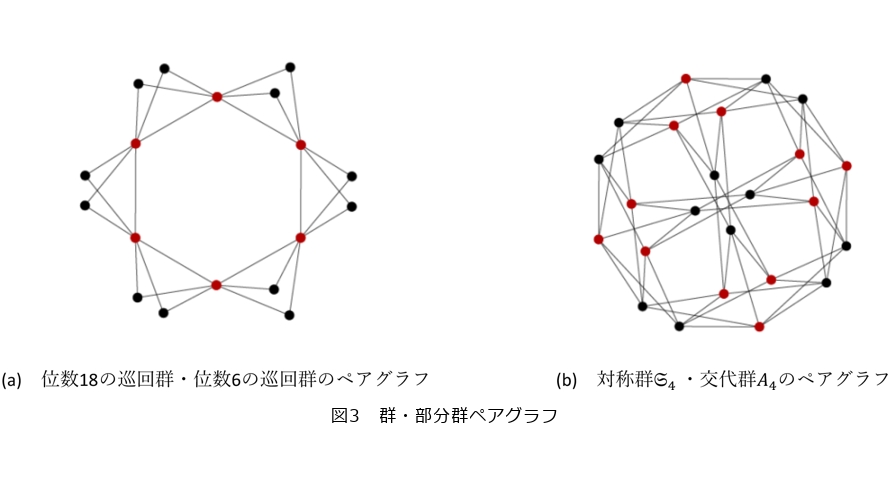
新しい方向としては、ケーリーグラフの拡張である群・部分群ペアグラフ(有限群とその部分群および群の適当な生成系から定まるグラフ、図3に対してハッシュ関数を定義し、その暗号学的な安全性に関する問題の定式化があります(18)。ここで群・部分群ペアグラフ ![]() (
( ![]() ,
, ![]() ,
, ![]() ) とは、群
) とは、群 ![]() とその部分群
とその部分群 ![]() 、そして
、そして![]() ∩
∩ ![]() が対称となる部分集合
が対称となる部分集合 ![]() ⊂
⊂ ![]() をとりケーリーグラフのように定義される一般には非正則なグラフです。まり
をとりケーリーグラフのように定義される一般には非正則なグラフです。まり ![]() (
( ![]() ,
, ![]() ,
, ![]() ) は
) は![]() の各元を頂点として
の各元を頂点として ![]() ∈
∈ ![]() と
と ![]() ∈
∈ ![]() に対して条件
に対して条件![]() ∼
∼ ![]() ⇔
⇔ ![]() =
= ![]() (
( ![]() ∈
∈ ![]() )なる関係∼を満たすとき辺としてつないでできるグラフです(19)。群・部分群ペアグラフによりラマヌジャングラフを構成することができますが、無限族の構成には至っていません(図3(b))。応用上も背後の数学の進歩という点からも無限族の構成は大きな目標です。
)なる関係∼を満たすとき辺としてつないでできるグラフです(19)。群・部分群ペアグラフによりラマヌジャングラフを構成することができますが、無限族の構成には至っていません(図3(b))。応用上も背後の数学の進歩という点からも無限族の構成は大きな目標です。
正の特異値をめぐって:Wishart 分布、Wallach 集合、α-行列の正値性
負の特異値に対するリース行列と同様に、![]() =
= ![]() のときに期待されるパーマネント的な構造の研究は自然です。探究のヒントになりそうなことを述べて本稿を閉じたいと思います。ユークリッド空間における凸錐上の正定値関数を考えることは最適化問題にも応用があります。ところで、対称錐上(リー群の対称空間)の正則関数がなすヒルベルト空間の解析、ユニタリ表現論において、いわゆる Wallach 集合という重要で一般的な概念があります。対称錐上の積分核においてWallach集合は本質的に正の特異値
のときに期待されるパーマネント的な構造の研究は自然です。探究のヒントになりそうなことを述べて本稿を閉じたいと思います。ユークリッド空間における凸錐上の正定値関数を考えることは最適化問題にも応用があります。ところで、対称錐上(リー群の対称空間)の正則関数がなすヒルベルト空間の解析、ユニタリ表現論において、いわゆる Wallach 集合という重要で一般的な概念があります。対称錐上の積分核においてWallach集合は本質的に正の特異値 ![]() の逆数たちで与えられます(20)。
の逆数たちで与えられます(20)。
統計学にWishart分布というものがあります。それは ![]() 二乗分布の多変数一般化であり、半正定値対称行列に対する分布です。互いに独立な
二乗分布の多変数一般化であり、半正定値対称行列に対する分布です。互いに独立な ![]() 個の
個の ![]() 変量の確率ベクトル
変量の確率ベクトル ![]() (
( ![]() ≥
≥ ![]() ) が、平均が0、共分散行列が
) が、平均が0、共分散行列が ![]() の多変量正規分布
の多変量正規分布 ![]() (0,
(0, ![]() ) に従うとき、
) に従うとき、![]() =
= ![]() は自由度
は自由度 ![]() のWishart 分布に従います。Wishart分布は標本サイズでスケーリングされた後、多変量正規乱数データに対する標本の共分散行列の分布のモデルとして多くの場合に使用される重要な分布です。Wishart分布は対称半正定値行列がなす対称錐との関係から、いわゆるジョルダン代数の表現論(20)の応用分野の1つです。一方で、
のWishart 分布に従います。Wishart分布は標本サイズでスケーリングされた後、多変量正規乱数データに対する標本の共分散行列の分布のモデルとして多くの場合に使用される重要な分布です。Wishart分布は対称半正定値行列がなす対称錐との関係から、いわゆるジョルダン代数の表現論(20)の応用分野の1つです。一方で、![]() - 行列式はこのWishart分布を用いての確率論的な表示を持つことが知られています(21)。このことを利用して白井は、非負定値の実対称、あるいはエルミート行列の場合に
- 行列式はこのWishart分布を用いての確率論的な表示を持つことが知られています(21)。このことを利用して白井は、非負定値の実対称、あるいはエルミート行列の場合に ![]() がそれぞれ
がそれぞれ ![]() 、
、![]() のときにその
のときにその ![]() - 行列式の非負定値性を示しました。証明にはJack多項式(7)といわれる重要な対称関数による議論が要となっています。本質的に、これらの値は本稿の負の特異値に一致しています。理由の解明が必要です。
- 行列式の非負定値性を示しました。証明にはJack多項式(7)といわれる重要な対称関数による議論が要となっています。本質的に、これらの値は本稿の負の特異値に一致しています。理由の解明が必要です。
■参考文献
(1) T. Shirai and Y. Takahashi:“Random point fields associated with certain Fredholm determinants I: Fermion, Poisson and boson point processes.” J. Funct. Anal., Vol. 205, pp. 414-463, 2003.
(2) D. Vere-Jones:“A generalization of permanents and determinants,”Linear Algebra Appl., Vol. 63, pp. 267-270, 1988.
(3) S. Matsumoto and M. Wakayama:“Alpha-determinant cyclic modules of ![]() ”J. Lie Theory, Vol.16, pp. 393-405, 2006.
”J. Lie Theory, Vol.16, pp. 393-405, 2006.
(4) D. Vere-Jones:“Alpha-permanents and their applications to multivariate gamma, negative binomial and ordinary binomial distributions,”New Zealand J. Math., Vol. 26, pp. 125-149, 1997.
(5) W. Fulton and J. Harris:“Representation Theory:A First Course(Graduate Texts in Mathematics, 129), Springer, 1991(木本(訳):“フルトン-ハリス表現論入門 上・下,”丸善出版, 2023-24).
(6) K. Kimoto, S. Matsumoto, and M. Wakayama:“Alpha-determinant cyclic modules and Jacobi polynomials.” Trans. Amer. Math. Soc., Vol.361, pp. 6447-6473, 2009.
(7) I. G. Macdonald:“Symmetric functions and Hall polynomials,”Oxford Univ. Press, Oxford. 1979.
(8) K. Kimoto and M. Wakayama:“Invariant theory for singular ![]() -determinants,”J. Combin. Theory Ser. A, Vol.115, pp. 1-31, 2008.
-determinants,”J. Combin. Theory Ser. A, Vol.115, pp. 1-31, 2008.
(9) K. Kimoto and M. Wakayama:“Quantum ![]() -determinant cyclic modules of
-determinant cyclic modules of ![]() , ”J. Algebra, Vol.313, pp. 922-956, 2007.
, ”J. Algebra, Vol.313, pp. 922-956, 2007.
(10) K. Kimoto:“Quantum alpha-determinants and ![]() -deformed hypergeometric polynomials,”Int. Math. Res. Not., Vol. 2009, No. 22, pp. 4168-4182, 2009.
-deformed hypergeometric polynomials,”Int. Math. Res. Not., Vol. 2009, No. 22, pp. 4168-4182, 2009.
(11) K. Kimoto:“Quantum ![]() -determinants and
-determinants and ![]() -deformations of hypergeometric polynomials,”RIMS Kokyuroku Bessatsu, Vol. B36, pp. 97-111, 2012.
-deformations of hypergeometric polynomials,”RIMS Kokyuroku Bessatsu, Vol. B36, pp. 97-111, 2012.
(12) 木本:“対称群上の帯球関数とリース行列式,”数理解析研究所講究録, Vol. 2031 , pp. 218-234, 2017.
(13) K. Hamamoto, K. Kimoto, H. Tachibana, and M. Wakayama:“Wreath determinants for group-subgroup pairs,”J. Combin. Theory Ser. A, Vol.133, pp. 76-96, 2015.
(14) B. Friedman and S. McGuinness:“The Alon-Tarsi conjecture: A perspective on the main results,”Discrete Math., Vol.342,No.8,pp. 2234-2253, 2019.
(15) 木本:“ラテン方陣に関するAlon-Tarsi予想と対称群上の帯球関数について,”数理解析研究所講究録, Vol.2039, pp. 193-210, 2017.
(16) K. Kimoto:“Wreath determinants, zonal spherical functions on symmetric groups and the Alon-Tarsi conjecture.”Ryukyu Math. J., Vol.34, pp. 5-19, 2021.
(17) J. H. van Lint and R. M. Wilson:“A Course in Combinatorics(2nd ed.),”Cambridge University Press, 2001.
(18) C. Reyes-Bustos:“Towards hash functions based on group-subgroup pair graphs. in“Mathematical Foundations for Post-Quantum Cryptography",” Springer, 2024.
(19) C. Reyes-Bustos:“Cayley-type graphs for group-subgroup pairs.”Linear Algebra Appl., Vol. 488, pp. 320-349, 2016.
(20) J. Faraut and A. Koranyi:“Analysis on Symmetric Cones(Oxford Mathematical Monographs),”Oxford,1995.
(21) T. Shirai:“Remarks on the positivity of ![]() -determinants.”Kyushu J. Math., Vol. 61, pp. 169-189, 2007.
-determinants.”Kyushu J. Math., Vol. 61, pp. 169-189, 2007.

(左から)Cid Reyes-Bustos/若山 正人







ごく特殊なものに着目することから始めるものの、表現論を通して多様に広がっていく数学研究の一端を見ていただければと思い本稿を執筆しました。ご紹介したのは一部ですが、解くべき問題は山積みです。