2024年7月号
特集
保型形式とフーリエ展開
- 保型形式
- フーリエ解析
- 表現論
フーリエ解析は現代社会においてなくてはならない技術ですが、数学においても同様です。本稿では、保型形式の歴史を振り返りながら、表現論とフーリエ解析そして保型形式のかかわりについて考察します。難しい用語の説明は脚注にとどめ、概念間の関係性に注目しました。最後に、現代の保型形式論に残り続ける困難について述べ、その課題と著者の研究の関係について議論します。
堀永 周司(ほりなが しゅうじ)
NTT基礎数学研究センタ
保型形式の歴史と課題
■保型形式の誕生
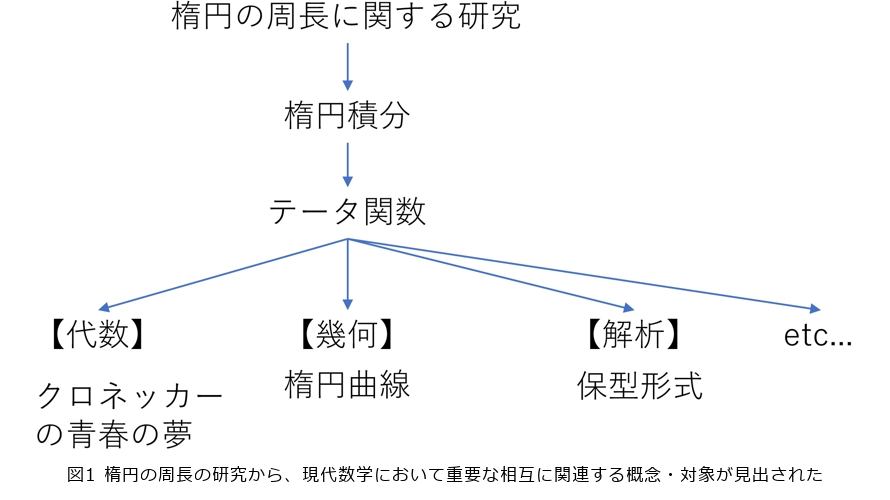
保型形式*1は、1800年ごろの楕円関数の研究に起源をもちます。当時は天文学が急速に発展している時節であり、天体観測技術が大幅に高精度化され始めていました。天体は楕円軌道を描くため、その周長を考える必要が出てきます。円の周長は円周率から容易に計算可能ですが、楕円の場合は大変難しく、(第二種)楕円積分を考える必要があります。ルジャンドル、ガウスやアーベルらによる研究を通じて、楕円積分は単に楕円の周長というだけでなく、現代の数学へと通ずる非常に興味深いものへと変貌していきました。その1つがテータ関数です。テータ関数は現在さまざまな数学に現れます。本稿のメインテーマである保型形式の一例でもありますし、そのほか楕円曲線や整数論においても現れます(図1、2)。別の応用として、1800年代後半に活躍したクロネッカーはテータ関数を用いて虚二次体の類体の構成を行いました。この仕事は「クロネッカーの青春の夢」と呼ばれ、現在ヒルベルトの第十二問題*2と関係する大変重要な結果です。このようにして、保型形式は具体例の研究を主としながら 1800 年代に誕生しました。
*1 保型形式:存在するかすらも当たり前ではない強烈な変換則を持った関数です。後に定義を行いますが、定義からはすぐには分からない整数論的に大変興味深い性質を多々持っています。
*2 ヒルベルトの第十二問題:ドイツ人数学者ダフィット・ヒルベルトが1900年に提示した 23の問題の1つです。それらは現在の数学の基礎の形成に大きな役割を果たしました。ヒルベルトの提示から 100年以上経った今でも、それら問題のうち完全に解決したものは半分もありません。
■保型形式論の発展と課題
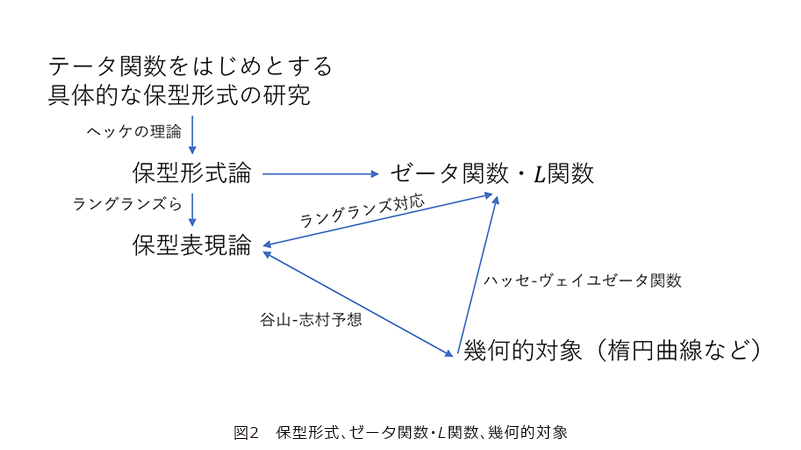
さらなる保型形式の発展には、ヒルベルトの学生であったヘッケの仕事を待たなければいけませんでした。もちろん、ヘッケ以前にもラマヌジャンなどによる仕事は多々あります。ヘッケはそれらをまとめ、保型形式論というものに落とし込みました。特に、ヘッケの仕事とリーマンゼータ関数の場合を基に保型形式からゼータ関数・![]() 関数が定義され、現代的な保型形式論への道筋が大きく拓かれました。そして、ラングランズらを通じて保型表現論へと発展しました。また、保型形式の歴史を振り返るうえで谷山-志村予想は欠かせないでしょう。谷山-志村予想は保型形式と楕円曲線をつなぐ深遠な予想です。ワイルズは谷山-志村予想の半安定という場合を解決し、フェルマ予想を完全に証明しました。現在では谷山-志村予想も完全に解決しており、その発展であるパラモジュラ予想も解決されてきています。これら予想の定式化には保型表現が欠かせません。そして、保型表現の研究が本質的な役割を果たしています。
関数が定義され、現代的な保型形式論への道筋が大きく拓かれました。そして、ラングランズらを通じて保型表現論へと発展しました。また、保型形式の歴史を振り返るうえで谷山-志村予想は欠かせないでしょう。谷山-志村予想は保型形式と楕円曲線をつなぐ深遠な予想です。ワイルズは谷山-志村予想の半安定という場合を解決し、フェルマ予想を完全に証明しました。現在では谷山-志村予想も完全に解決しており、その発展であるパラモジュラ予想も解決されてきています。これら予想の定式化には保型表現が欠かせません。そして、保型表現の研究が本質的な役割を果たしています。
谷山-志村予想は解析的な対象である保型形式と幾何的な対象である楕円曲線を結ぶものでした。ラングランズや志村をはじめとする多くの研究者による膨大で緻密な研究を通じて、谷山-志村予想は当初の姿を大きく超え、代数・幾何・解析の統一理論といった様相を呈してきています。しかしながら、保型形式論には依然として残る大きな課題があります。それは非正則な保型形式論の研究です。谷山と志村は、正則保型形式のフーリエ係数の計算結果が多数知られていることを基に、谷山-志村予想を定式化できました。しかし、非正則な保型形式ついてはそのフーリエ係数の例すらもほとんど知られていません。そのような例の不足がさらなる発展の障害となっています。谷山-志村予想や球面充填問題*3のように、非正則な保型形式が多様な応用を持つことは想像に難くありませんが、保型形式側の発展が不足しています。本稿では、フーリエ展開と表現論のかかわりを確認し、その発展ともいえるラングランズ予想やアーサー予想に触れ、最後に非正則な保型形式のフーリエ展開に関する著者と早稲田大学成田宏秋教授との共同研究について紹介します。
*3 球面充填問題:同じ半径の球を使って空間をどの程度埋め尽くすことが可能か、という問題です。マリナ・ヴィヤゾフスカは 8次元と24次元の場合に当問題を保型形式を用いて解決し、2022年にフィールズ賞を獲得しました。
フーリエ展開と表現論
■フーリエ展開
フーリエ展開やフーリエ変換という言葉を耳にした人は多いのではないでしょうか。フーリエ変換は1800年ごろ熱伝導方程式を解くためにフーリエによって導入されました。それらは現代社会に必須の技術の1つであり、例えば、音の信号を処理する際によく用いられます。どんな複雑な音でも、テレビやラジオの時報の音のような単純な音を混ぜていくことでつくれる、というのがその考え方です。この単純な音は数学的に ![]() 関数や
関数や ![]() 関数などの三角関数です。数学的には、フーリエ展開は周期関数を
関数などの三角関数です。数学的には、フーリエ展開は周期関数を ![]() や
や ![]() の無限和に展開することを指し、フーリエ変換はその展開に現れる係数を指します。そして、フーリエ展開は数学において現代でさえも、技術的・理論的側面の両面において重大な役割を果たしています。
の無限和に展開することを指し、フーリエ変換はその展開に現れる係数を指します。そして、フーリエ展開は数学において現代でさえも、技術的・理論的側面の両面において重大な役割を果たしています。
まずはフーリエ解析と表現論のかかわりについて観察しましょう。フーリエ展開やフーリエ変換は、周期関数への平行移動を通じて周期関数全体を理解しようという取り組みであるといえます。それらを明確にするために、数学的な詳細に立ち入っていきましょう。 ![]() を実数
を実数 ![]() 上の複素数値関数とします。
上の複素数値関数とします。![]() が周期1を持つとは、
が周期1を持つとは、![]() となることをいいます。ゆえに、周期関数は
となることをいいます。ゆえに、周期関数は ![]() 上の関数と考えることができます。このような周期関数
上の関数と考えることができます。このような周期関数 ![]() を三角関数
を三角関数 ![]() を用いて表すのがフーリエ展開の理論です。もっと精密には、
を用いて表すのがフーリエ展開の理論です。もっと精密には、![]() を通じて
を通じて
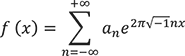
という無限個の和に関数 ![]() を分解することを
を分解することを ![]() のフーリエ展開といいます。現れる係数
のフーリエ展開といいます。現れる係数 ![]() がフーリエ係数です。
がフーリエ係数です。![]() は
は ![]() のフーリエ変換
のフーリエ変換 ![]() を用いて
を用いて ![]() とも表されます。表現論では、周期関数のような性質を持った数学的な対象たちを、より細かい性質をもって切り分けることを行います。典型的な例として、行列のベクトル空間への作用を考えましょう。その行列の作用を固有値と固有ベクトルに分けることで、もともとの行列に対する理解が大きく進みます。このような、行列から固有値や固有ベクトルを得るような一連の大きな枠組みが表現論の1つの側面です。
とも表されます。表現論では、周期関数のような性質を持った数学的な対象たちを、より細かい性質をもって切り分けることを行います。典型的な例として、行列のベクトル空間への作用を考えましょう。その行列の作用を固有値と固有ベクトルに分けることで、もともとの行列に対する理解が大きく進みます。このような、行列から固有値や固有ベクトルを得るような一連の大きな枠組みが表現論の1つの側面です。
では、フーリエ解析と表現論について観察しましょう。上記の表現論の考え方に照らし合わせますと、ベクトル空間として周期関数全体、作用する行列として以下で述べる平行移動というものを考えます。周期関数 ![]() に対して実数
に対して実数 ![]() による平行移動
による平行移動 ![]() を考えると、平行移動した関数
を考えると、平行移動した関数 ![]() のフーリエ展開の
のフーリエ展開の ![]() 番目のフーリエ係数は
番目のフーリエ係数は ![]() に一致します。つまり、
に一致します。つまり、 ![]() に関する平行移動がなす作用は、
に関する平行移動がなす作用は、![]() という関数を固有ベクトル、
という関数を固有ベクトル、 ![]() を固有値としていると考えられます。まとめると、周期関数とそのフーリエ展開に平行移動という表現を組み合わせることで次が対応することが結論付けられます。
を固有値としていると考えられます。まとめると、周期関数とそのフーリエ展開に平行移動という表現を組み合わせることで次が対応することが結論付けられます。
・![]() 上の表現で
上の表現で ![]() と表されるもの
と表されるもの
・ 周期関数のフーリエ展開に現れる ![]() 番目の項
番目の項
表現という一見するとよく分からないものと関数を結び付けることにより、表現の1つのカオをとらえることができました。この驚くべき対応は ![]() というシンプルな群だけでなく、より広い枠組みでとらえることが可能です。その様子を次で観察しましょう。
というシンプルな群だけでなく、より広い枠組みでとらえることが可能です。その様子を次で観察しましょう。
■フーリエ解析からラングランズ予想へ
関数を通じた表現の理解は ![]() という周期関数に対応する場合は深く理解が可能でした。その理由は
という周期関数に対応する場合は深く理解が可能でした。その理由は ![]() がコンパクトという性質を持っていることに由来します。非コンパクトな対象、例えば実数全体
がコンパクトという性質を持っていることに由来します。非コンパクトな対象、例えば実数全体 ![]() では積分の収束をはじめとする技術的困難から数学的に大変に難しくなっていきます。その様子は、フーリエ解析の本において、周期関数のフーリエ解析と実数
では積分の収束をはじめとする技術的困難から数学的に大変に難しくなっていきます。その様子は、フーリエ解析の本において、周期関数のフーリエ解析と実数 ![]() 上の関数のフーリエ解析では扱いの差からも理解可能です。これらの差異は主に
上の関数のフーリエ解析では扱いの差からも理解可能です。これらの差異は主に ![]() はコンパクトであり
はコンパクトであり ![]() は非コンパクトであるという数学的事実から来ているのです。
は非コンパクトであるという数学的事実から来ているのです。
非コンパクト群の表現論を大きく進めた立役者の1人がハリシュチャンドラです。ハリシュチャンドラは、主にリー群という ![]() や
や ![]() を含む群を扱いました。特に顕著な仕事としては、離散系列表現の分類が挙げられます。それは、
を含む群を扱いました。特に顕著な仕事としては、離散系列表現の分類が挙げられます。それは、![]() や
や ![]() では関数空間を考えたように、非コンパクト群
では関数空間を考えたように、非コンパクト群 ![]() に対して
に対して ![]() という
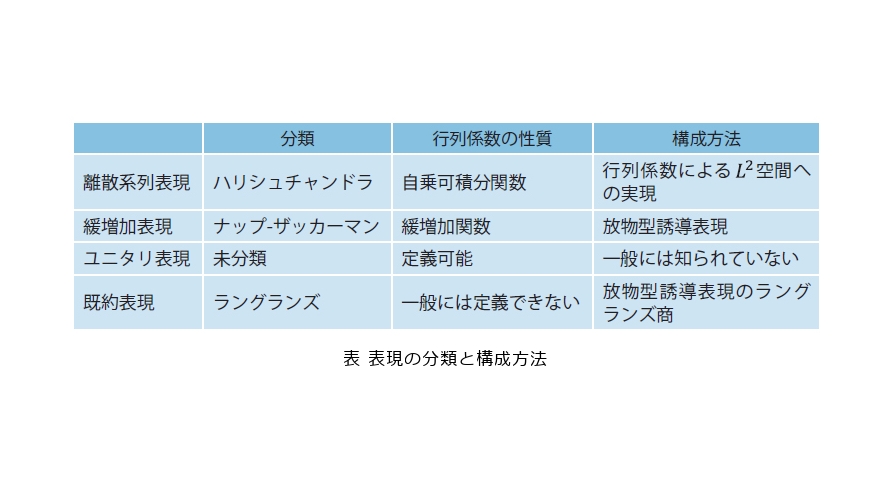
という ![]() の自乗可積分関数全体*4とそれ上の平行移動を考えた際に自然に現れるものです。これらの対応は表現の行列係数*5を通じて得られます。このように、表現論は関数空間とその解析を背景として大きく発展しました。ハリシュチャンドラの仕事を基本として、ナップとザッカーマンはリー群の緩増加表現の分類を行い、それを土台としてラングランズは一般の既約表現の分類を行いました(表)。このラングランズの分類を端的にラングランズ分類といいます。リー群とは実数
の自乗可積分関数全体*4とそれ上の平行移動を考えた際に自然に現れるものです。これらの対応は表現の行列係数*5を通じて得られます。このように、表現論は関数空間とその解析を背景として大きく発展しました。ハリシュチャンドラの仕事を基本として、ナップとザッカーマンはリー群の緩増加表現の分類を行い、それを土台としてラングランズは一般の既約表現の分類を行いました(表)。このラングランズの分類を端的にラングランズ分類といいます。リー群とは実数 ![]() や複素数
や複素数 ![]() 上での理論ですから、整数論の研究者は実数の類似である
上での理論ですから、整数論の研究者は実数の類似である ![]() 進数体
進数体 ![]() などでの類似の理論を渇望していました。
などでの類似の理論を渇望していました。
さまざまな試行錯誤を通じ、![]() 進数体上の群の既約表現の分類に関する予想である局所ラングランズ予想が定式化されていきました。局所ラングランズ予想とは、連結簡約代数群*6
進数体上の群の既約表現の分類に関する予想である局所ラングランズ予想が定式化されていきました。局所ラングランズ予想とは、連結簡約代数群*6 ![]() に対する次のような対象の間の対応です:
に対する次のような対象の間の対応です:
![]()
右辺の ![]() パラメータという部分が数論的な対象であり、
パラメータという部分が数論的な対象であり、![]() 関数を定めます。本特集記事『数論・代数幾何・表現論が紡ぐ数学の世界』(1)にあるとおりラングランズ予想は非可換類体論としての側面を持つのですが、それが右辺の
関数を定めます。本特集記事『数論・代数幾何・表現論が紡ぐ数学の世界』(1)にあるとおりラングランズ予想は非可換類体論としての側面を持つのですが、それが右辺の ![]() パラメータの部分に現れているのです。現在、局所ラングランズ予想は大きく進展してきており、内視鏡的分類の理論(endoscopic classification)などのより精密な予想へと発展してきています。そして、
パラメータの部分に現れているのです。現在、局所ラングランズ予想は大きく進展してきており、内視鏡的分類の理論(endoscopic classification)などのより精密な予想へと発展してきています。そして、![]() 進体上の群の表現論と保型形式は切っても切り離せません。事実、互いに短所を補い合いながらともに発展してきた歴史があります。最後に、保型形式のフーリエ展開と非正則な保型形式に関する著者の結果について述べていきましょう。
進体上の群の表現論と保型形式は切っても切り離せません。事実、互いに短所を補い合いながらともに発展してきた歴史があります。最後に、保型形式のフーリエ展開と非正則な保型形式に関する著者の結果について述べていきましょう。
*4 自乗可積分関数全体:![]() となる関数
となる関数 ![]() 全体。
全体。
*5 表現の行列係数:表現は一般に無限次の行列より実現されます。その行列の成分を行列係数といいます。
*6 連結簡約代数群:代数群とは代数多様体であり群となるものです。連結とは代数多様体としての連結性を意味し、簡約とは群のクラスを指します。例えば一般線形群や直交群やユニタリ群は連結簡約代数群となっています。しかし、上三角行列などは簡約群ではありません。
保型形式と表現論
■正則保型形式のフーリエ展開
正則保型形式のフーリエ展開・フーリエ係数について観察します。![]() を上半平面*7とします。このとき、
を上半平面*7とします。このとき、![]() に対して特殊線型群
に対して特殊線型群![]() *8が一次分数変換*9で作用します。次に、
*8が一次分数変換*9で作用します。次に、 ![]() の中で成分がすべて整数のものを
の中で成分がすべて整数のものを ![]() と表しましょう。
と表しましょう。![]() を保型因子*10とします。
を保型因子*10とします。![]() を整数とし、
を整数とし、![]() を
を ![]() 上の正則関数とします。このとき、
上の正則関数とします。このとき、![]() が重さ
が重さ ![]() の
の ![]() に関する保型形式*11とは、
に関する保型形式*11とは、![]() に対して
に対して ![]() となることをいいます。つまり、
となることをいいます。つまり、![]() の作用について完全に不変ではなく、多少のお釣り
の作用について完全に不変ではなく、多少のお釣り ![]() が出てくるような関数です。特に、
が出てくるような関数です。特に、![]() が分かりますから、虚部
が分かりますから、虚部 ![]() を固定するごとにフーリエ展開が可能です。
を固定するごとにフーリエ展開が可能です。![]() が正則関数であることから、コーシーの積分公式を通じ、以下のフーリエ展開が可能です:
が正則関数であることから、コーシーの積分公式を通じ、以下のフーリエ展開が可能です:
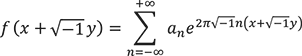
驚くことに、この表示であれば係数 ![]() は虚部
は虚部 ![]() に依存しません。この展開式を
に依存しません。この展開式を ![]() のフーリエ展開、
のフーリエ展開、![]() を保型形式
を保型形式 ![]() のフーリエ係数といいます。
のフーリエ係数といいます。
*7 上半平面:複素数のうち虚部が正のもの全体。
*8 特殊線型群:2×2の実数係数行列で行列式が1であるもの全体。
*9 一次分数変換: ![]() に対して
に対して ![]() としたもの。
としたもの。
*10 保型因子:![]() に対して
に対して ![]() としたもの。
としたもの。
*11 保型形式:厳密には、この定義では保型形式にはならず、準保型形式というものにしかなりません。準保型形式 ![]() が保型形式とは、
が保型形式とは、![]() の
の ![]() 番目のフーリエ係数
番目のフーリエ係数 ![]() が
が ![]() のとき
のとき ![]() をなすことをいいます。
をなすことをいいます。
■保型形式と表現論
関数空間への平行移動が表現論と強くかかわることを前述のフーリエ展開で観察しました。同様の事象が保型形式でも発生します。つまり、保型形式をリー群の商空間上の関数へ持ち上げることが可能です。それにより保型形式 ![]() を持ち上げた関数
を持ち上げた関数 ![]() は
は ![]() の元となります。フーリエ展開で観察したように、この空間は
の元となります。フーリエ展開で観察したように、この空間は ![]() の平行移動を考えることが可能ですから、リー群
の平行移動を考えることが可能ですから、リー群 ![]() の表現論と関連します。さらに進めると、有理数体
の表現論と関連します。さらに進めると、有理数体 ![]() のアデール環
のアデール環 ![]() と呼ばれるものを用いて、保型形式はアデール群
と呼ばれるものを用いて、保型形式はアデール群 ![]() 上の滑らかな関数
上の滑らかな関数 ![]() となります。
となります。![]() が自乗可積分であるならば、少なくとも尖点形式ならば、
が自乗可積分であるならば、少なくとも尖点形式ならば、![]() の元
の元 ![]() です。つまり、自乗可積分な保型形式
です。つまり、自乗可積分な保型形式 ![]() から自乗可積分関数の空間
から自乗可積分関数の空間 ![]() の元が自然に得られ、その関数空間にはフーリエ解析の場合と同様にリー群
の元が自然に得られ、その関数空間にはフーリエ解析の場合と同様にリー群 ![]() や
や ![]() 進体上の群
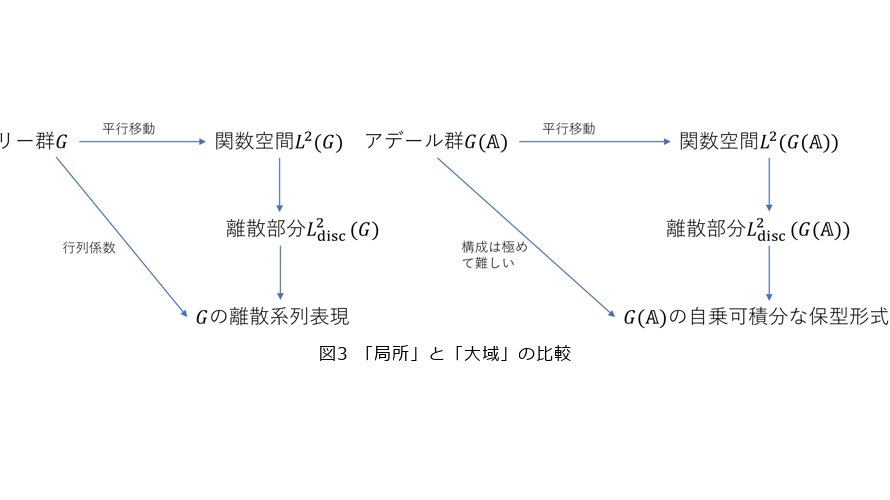
進体上の群 ![]() の表現論が現れるのです。この現象はフーリエ変換と表現論の結び付きの際に現れたものと同じ現象です (図3)。現代の保型形式論では、
の表現論が現れるのです。この現象はフーリエ変換と表現論の結び付きの際に現れたものと同じ現象です (図3)。現代の保型形式論では、![]() の
の ![]() の部分を連結簡約代数群に一般化して考えます。ハリシュチャンドラが離散系列表現を考えたように、
の部分を連結簡約代数群に一般化して考えます。ハリシュチャンドラが離散系列表現を考えたように、![]() にも離散的な部分を考えることができます。その離散的な部分の記述が現在の保型形式論を用いると可能になってきました。それには、ラングランズの学生であったアーサーやシェルスタッドらによる研究が土台となっています。特に、アーサーは離散部分の記述であるアーサー予想を定式化し、群が斜交群や分裂直交群の場合に予想を適切な修正の下で証明しました。その研究は現在の保型形式論における最高峰の1つといってよいでしょう。現在、アーサーの仕事の拡張や応用が盛んに研究されています。
にも離散的な部分を考えることができます。その離散的な部分の記述が現在の保型形式論を用いると可能になってきました。それには、ラングランズの学生であったアーサーやシェルスタッドらによる研究が土台となっています。特に、アーサーは離散部分の記述であるアーサー予想を定式化し、群が斜交群や分裂直交群の場合に予想を適切な修正の下で証明しました。その研究は現在の保型形式論における最高峰の1つといってよいでしょう。現在、アーサーの仕事の拡張や応用が盛んに研究されています。
■保型形式のフーリエ展開の一般化に向けて
上半平面上の正則保型形式はフーリエ係数が定数となっています。しかし、この点は ![]() が正則という事実に強く依存しています。そのため、正則性を除いたとき、そのフーリエ展開は
が正則という事実に強く依存しています。そのため、正則性を除いたとき、そのフーリエ展開は
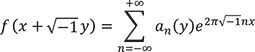
として係数 ![]() が
が ![]() に依存したかたちでしか書き下すことができません。そのため、係数
に依存したかたちでしか書き下すことができません。そのため、係数 ![]() の研究は大変な困難を伴います。著者と成田氏との共同研究(2)では、このような非正則な保型形式のフーリエ展開やフーリエ係数を扱いました。非正則な保型形式として典型的なものの1つはマース形式と呼ばれるものですが、それを扱わずに、より表現論的に自然な保型形式*12を考察したというのがポイントです。そのために、ハリシュチャンドラの離散系列表現の分類を考えてみましょう。これまで述べてきた上半平面上の保型形式とは
の研究は大変な困難を伴います。著者と成田氏との共同研究(2)では、このような非正則な保型形式のフーリエ展開やフーリエ係数を扱いました。非正則な保型形式として典型的なものの1つはマース形式と呼ばれるものですが、それを扱わずに、より表現論的に自然な保型形式*12を考察したというのがポイントです。そのために、ハリシュチャンドラの離散系列表現の分類を考えてみましょう。これまで述べてきた上半平面上の保型形式とは ![]() に対応する保型形式です。
に対応する保型形式です。![]() に対する離散系列表現はある意味で1つしかありません。マース形式の難しい点の1つは、そういった離散系列表現という素性の良い表現に対応しない部分ではないかと考えたのです。では、正則なものに対応しない離散系列表現を持つものは何か、というと、例えば次数2の斜交群
に対する離散系列表現はある意味で1つしかありません。マース形式の難しい点の1つは、そういった離散系列表現という素性の良い表現に対応しない部分ではないかと考えたのです。では、正則なものに対応しない離散系列表現を持つものは何か、というと、例えば次数2の斜交群 ![]() があります。
があります。![]() の場合はある意味で離散系列表現は2種類あり、1つは正則なものに対応しており、もう片方が非正則なものとなります。また、
の場合はある意味で離散系列表現は2種類あり、1つは正則なものに対応しており、もう片方が非正則なものとなります。また、![]() は離散系列表現を複数持つ群のうち、もっとも小さいものと考えることができます。
は離散系列表現を複数持つ群のうち、もっとも小さいものと考えることができます。![]() 上の保型形式は、次数2のジーゲル上半平面*13
上の保型形式は、次数2のジーゲル上半平面*13 ![]() 上の関数
上の関数 ![]() に対応し、フーリエ展開を持ちます。
に対応し、フーリエ展開を持ちます。
式(1)のフーリエ係数部分に現れる ![]() を一般化ホイッタッカー関数といいます。正則保型形式の場合と異なり、もはや定数とはなりません。離散系列表現を考える際の重要なポイントは
を一般化ホイッタッカー関数といいます。正則保型形式の場合と異なり、もはや定数とはなりません。離散系列表現を考える際の重要なポイントは ![]() の考察に微分方程式を導入できる点にあります。共同研究では、その微分方程式の解の性質を通じ、
の考察に微分方程式を導入できる点にあります。共同研究では、その微分方程式の解の性質を通じ、![]() の諸性質を導きました。応用として、
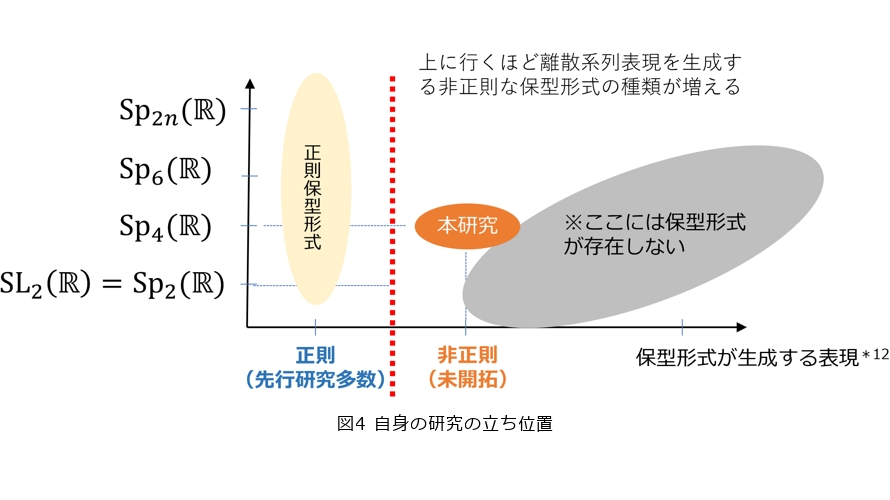
の諸性質を導きました。応用として、![]() の非尖点的保型形式で、
の非尖点的保型形式で、![]() 上の表現として離散系列表現を生成するものを完全に記述しました。図4にあるとおり、非正則な保型形式を構成方法も含めて記述する研究として、本研究は最初の一歩を踏み出したものとなっています。現在は、フーリエ展開の記述の次の仕事、つまりフーリエ係数の記述を考察しています。離散系列表現に対応する保型形式のフーリエ係数の具体的な考察を通じ、
上の表現として離散系列表現を生成するものを完全に記述しました。図4にあるとおり、非正則な保型形式を構成方法も含めて記述する研究として、本研究は最初の一歩を踏み出したものとなっています。現在は、フーリエ展開の記述の次の仕事、つまりフーリエ係数の記述を考察しています。離散系列表現に対応する保型形式のフーリエ係数の具体的な考察を通じ、![]() 関数の整数論的な性質を導くことを目標に、研究を推進しています。
関数の整数論的な性質を導くことを目標に、研究を推進しています。
*12 保型形式と表現:これまで述べたとおり、保型形式はそれを群上の関数に持ち上げることで表現に対応します。対応先の表現を ![]() としたとき、保型形式は
としたとき、保型形式は ![]() を生成するといいます。
を生成するといいます。
*13 ジーゲル上半平面:![]() と定義される空間。
と定義される空間。
■参考文献
(1) 佐野・宮﨑・若山:“数論・代数幾何・表現論が紡ぐ数学の世界,”NTT技術ジャーナル,Vol.36,No.7,pp.10-15,2024.
(2) S. Horinaga and H. Narita:“Cuspidal components of Siegel modular forms for large discrete series representations of ![]() ”manuscripta mathematica, pp.1-44,2023.
”manuscripta mathematica, pp.1-44,2023.

堀永 周司







フーリエ解析は現代社会でも、数学においても大変重要な対象です。その中でも表現論とのかかわりは大変興味深く、面白い理論となっています。本稿を通じて興味を抱いた数学用語や分野が1つでもありましたら幸いです。