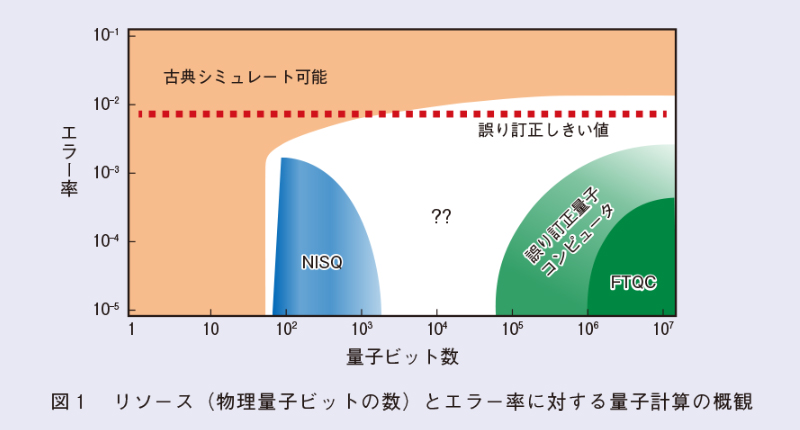
量子力学の原理が、従来技術では実現できない、あるいは従来技術の性能を大きく凌駕する、全く新しい技術を生み出すことが分かってから約半世紀になります。これら技術のすべては、「量子」の技術的優位性を獲得するために、「量子コヒーレンス＊1」や「量子もつれ＊2」を利用し、その応用範囲は量子計測・イメージングから、量子通信、量子計算に至るまでと、広範なものになっています。これらの分野自体は依然として揺籃期にありますが、私たちはすでに、量子センサアレイを含む多数の入力を取り入れ、量子コンピュータをつなぐ「量子インターネット」の姿さえも想像しています（1）。必要とあれば量子時計＊3を用いて、ここで使用されるすべてのデバイスを同期することもできます（2）。ここでの疑問は、図1にあるように、現在手に入る数量子ビットデバイスから、NISQ（Noisy Intermediate-Scale Quantum）プロセッサ（3）や、究極的な誤り耐性量子コンピュータ（4）にどのように移行していくか、あるいはこれらを実現するためにどのような道のりを歩むべきかということです。
ここ10年間で、量子技術の開発やその将来に関してのパラダイムシフトが起きてきました。一研究室レベルで、数量子ビットを用いて原理検証実験を行ってきたこれまでとは異なり、商用利用可能で、ある程度の規模を持つ量子プロセッサを構築するレベルへと移行してきました。超伝導回路、イオントラップ、光学系では、コヒーレンスを保ちながら同時に動作する約50量子ビットを持つデバイスが実現され、それらの上で非自明な量子アルゴリズムが実行されています。これらのNISQプロセッサは、従来型の計算機では計算することが困難な複雑性、いわゆる「量子優位性」を持つことが示されています（5）、（6）。しかし、NISQプロセッサで用いられる量子ビットやゲート操作、測定、制御が持つノイズの影響で、それが扱えるタスクのサイズは非常に制限されます（図１）。ノイズ補償技術は、システムサイズの拡大にある程度は貢献しますが、（10⁶から10⁸個の量子ビットと数兆回にも及ぶゲート操作から成る）万能量子計算までをも達成しようと思うと、誤り訂正や誤り耐性が必要になります。基本的な問いは、現状の技術動向をかんがみて、どのようにして量子コンピュータの未来像を獲得していくかということです。
図1は、リソース（物理量子ビットの数）とエラー率に対する量子計算の概観（7）です。橙色は実行するタスクが古典計算機でもシミュレート可能な領域、青色は量子優位性を示すタスクが存在する領域、薄緑色は量子誤り訂正符号を利用した量子コンピュータで遂行できるタスクの領域、深緑色は誤り耐性万能量子コンピュータ（FTQC：Fault Tolerant Quantum Computer）で遂行できるタスクの領域をそれぞれ表しています。

＊1 量子コヒーレンス：量子力学に従う系の状態は、波のような性質を持つ波動関数を使ってしか表現できないことがあります。この状態は「量子コヒーレンスを持つ」とみなされます。
＊2 量子もつれ：複数粒子の状態が、部分系の記述をどんなに巧みに持ち寄っても決して表現できない、量子力学特有の現象。量子通信、量子計算のリソース。光子や原子などを用いて、その存在はすでに実験で確認されています。
＊3 量子時計：不確定さが量子力学的限界に到達している原子時計。

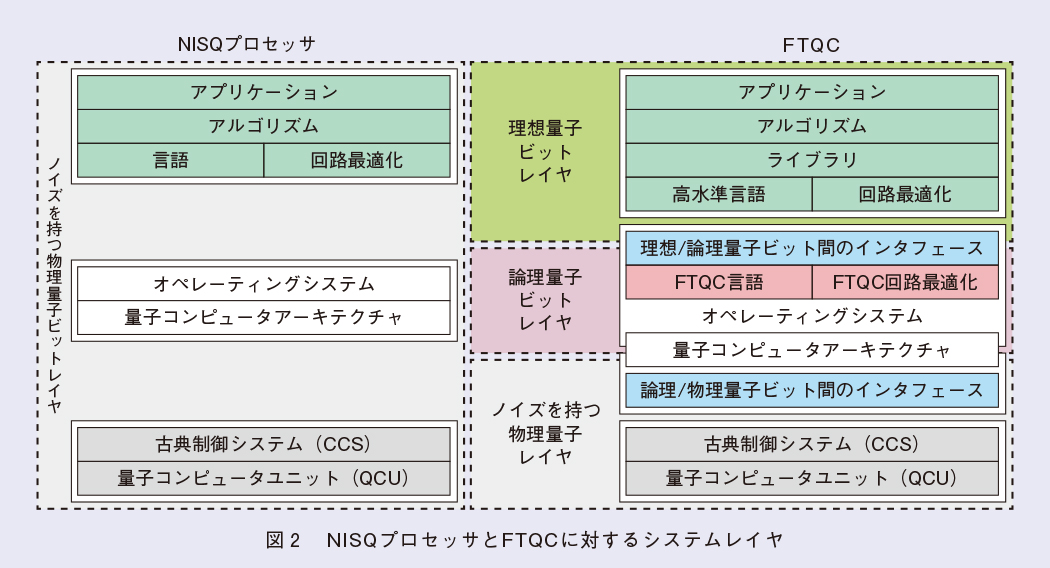
量子コンピュータのデザインについて、NISQプロセッサとシミュレータに関する考察から始めます。それらは、特定の範囲のタスクに着手するようにデザインされた完全にプログラマブルなマシンであり、理想的には万能性を有しますが、ノイズの影響により用途が専用マシンへと制限されます。しかし、NISQプロセッサやシミュレータは量子物理が提供する潜在能力を明らかにするには極めて有用です。もっとも開発が進んでいる超伝導回路やイオントラップを用いて、NISQプロセッサを構成する取り組みは数多く存在します（3）。しかし、プロセッサやシミュレータは、ある特定の様態で一緒に動作する20から100個の量子ビットの集合体に過ぎません。それらは、図2の各層として描かれている異なるレベルのシステムを、シームレスかつ一緒に動作するように統合したデバイスです。最上位層には、NISQプロセッサ上で実行させたいアプリケーション（シミュレーションやサンプリングなど）があります。アプリケーションは非常に抽象的なオブジェクトで、タスクを遂行するのに必要なインストラクションやルールを与えるアルゴリズムに翻訳されます。これらのインストラクションは、プロセッサが実行する基本演算（ゲート操作や測定など）のセットに分解されます。そのような基本演算は抽象化されていて、ハードウェアに依存するものではありません。オペレーティングシステムは、そのような基本演算の列を受けて、それらを与えられたプロセッサアーキテクチャ上でどのように実行するかを決めます。ここで、NISQプロセッサの設計や接続性が、実行可能なアルゴリズムを決定します。オペレーティングシステムは、そのアルゴリズムを受け、古典制御システム（CCS）が量子コンピュータユニット（QCU）上でそのアルゴリズムを実行させるための「物理的な指示パルス・シグナル」へと翻訳します。サイズの小さいプロセッサの多くに対しては、オペレーティングシステムや、アーキテクチャ以上の上位層はシステムに統合されずに、その役割はオフラインで、（時には手作業で）行われることもあります。
しかし、プロセッサの量子ビットの数が増えるにつれて、これらはプロセッサの処理能力への制限となるため、上位層の統合も重要となっていきます。ゲート操作や測定などの基本演算の列の最適化は、プログラムを実行させる物理系のノイズの影響を最小化するために、アルゴリズムとオペレーティングシステムを合わせて行われる必要があります。最終的には、量子ビットのコヒーレンス時間、ゲート操作や測定の質が、可能な計算のサイズを制限します。つまり、解きたい問題に対するNISQプロセッサの有用性は、プロセッサ中のエラーそのものによって制限されるのです。例えば100量子ビットのプロセッサ上で、各々の量子ビットに100回のゲート操作を行う場合、１ゲート操作当りのエラーとして10⁻⁴という低い誤り率を考慮するだけでも、ほぼ確実にエラーを含む計算結果しか得られないということになってしまいます。
NISQプロセッサやシミュレータの開発は、大規模万能量子コンピュータの実現をめざす上でも重要なステップです。NISQプロセッサはすでに量子優位性（ある程度の数の量子ビットしか持たない量子プロセッサであっても、数兆個のトランジスタを用いた今日のスーパーコンピュータよりも高速に、何かしらのタスクを遂行し得ること）を示しています。このことは、量子的なアプローチが持つ潜在能力を示した点で重要です。そして、これらNISQプロセッサでの成果が、量子コンピュータにおけるシステム全体の構成やレイヤデザイン、またそれらが現実にどのように動作するのかを解明するというより大きな課題へと、研究のフォーカスに大きな転機をもたらしたことは特筆すべき重要な点でしょう。

ノイズ補償技術はある程度（おそらく数桁の）エラーの影響を低減しますが、より大規模なプロセッサに対してはスケールしません。そこで、プロセッサのノイズに対処する方法を確立する必要があります。量子誤り訂正符号＊4は、これを行うための不可欠な手法です。しかし、量子情報を、多数の物理量子ビットから構成される論理量子ビットに埋め込む必要があるため、そのリソースコストは大きくなります。図2において、誤り訂正量子コンピュータにはあって、NISQプロセッサにはないレイヤは、この量子誤り訂正機能の実装のために付加されています。これを付加することによって生じる技術的ギャップは、雑音を持つ（例えば、0.1％の誤り率を持つ）物理量子ビットを扱う場合でも、非常に大きく、必要な量子ビット数も桁違いに大きくなります。また、量子誤り訂正が機能するためのエラーしきい値を超えないようにシステムを動作させる必要があります。このような量子誤り訂正を利用するだけで、誤り耐性量子計算の実現以前に、意義ある応用が見つかるかもしれません。この可能性は十分に探索されていませんが、興味深い取り組みです。誤り訂正量子コンピュータは、後述する完全な誤り耐性量子コンピュータへの自然な橋渡しの役を演じます。

＊4 量子誤り訂正符号：複数の量子ビットを組み合わせ、エラー耐性を持つ（少数個の）量子ビットを構成する符号。

ここでは誤り耐性量子コンピュータを定義することから始めます。誤り耐性量子コンピュータとは、そのデザインを変更することなしに任意のサイズの計算が実行可能な誤り訂正量子コンピュータの具体形です。それは、NISQプロセッサのレイヤ構造のデザインに大きな変更を要求し、少なくともレイヤ構造を３つの部分に分ける必要があります。1つは雑音を持つ物理量子ビットレイヤ、もう1つは論理量子ビットレイヤ、そして最後の1つは理想量子ビットレイヤで、これらのレイヤは協調して動作する必要があります。
最上位レイヤ（図2中の緑色の層）は、NISQアプローチで示されたものと同様ですが、ライブラリを有し、高水準言語が割り当てられ、理想量子ビットに作用することが想定されます。ライブラリの目的は、アルゴリズムが使用する可能性のある有用なサブルーチンを提供することです。アルゴリズムは、理想的なゲート操作と理想的な測定の列、すなわち、理想的な量子回路に変換されます。回路圧縮技術は、必要とされる理想量子ビットや、暫定的に必要なリソースを減らすために利用されます。このレイヤは仮想量子マシンのようなもので、ハードウェアに依存しません。理想量子ビット上では、どんなゲート操作も施せます。
中間レイヤは、論理量子ビットとそれに対する操作に関与します。論理量子ビットは、実行できるゲート操作に制限があるという点で、前述の理想量子ビットとは異なります。中間レイヤは、理想量子ビットとのインタフェースの役を担い、理想量子ビットレイヤの量子回路（コード）を（制限されたゲート操作しか持たない）論理量子ビットに対するものに変換します。これらの論理量子ビットは、エラーしきい値以下で動作する物理量子ビットを用いた量子誤り訂正符号を基に定義されます。したがって、このレイヤでどの量子誤り訂正符号を用いるのかが示されます。これに付随し、量子計算の誤り訂正モデル（ブレーディングや格子サージェリーなど）や、それを記述する言語が決定されます（8）。これらの論理量子ビットに対する演算は、ノイズを持つ物理量子ビットレイヤに対する物理操作のセットへと分解されます。
最下位のレイヤ（ノイズを持つ物理量子ビットレイヤ）も、NISQプロセッサのそれと同様ですが、誤り耐性量子計算では、計算中に実行される演算は、より規則正しく、より均一なものが要求されます。最下位レイヤは、中間レイヤから与えられた物理量子ビットへの物理操作を受け取り、ハードウェアデバイスのレイアウトや接続性を考慮し、どのようにそれを実装するかを決定します。オペレーティングシステムは、そのアルゴリズムを受け、CCSがQCU上でそのアルゴリズムを実行させるための物理的な指示パルス・シグナルへと翻訳します。
これらのレイヤは別々に与えられますが、誤り耐性量子計算では、シームレスかつ一緒に動作する必要があります（4）。あるレイヤの小さな変更が他のレイヤの大きな変更につながる可能性もあります。例えば、中間レイヤにおける量子誤り訂正符号の選択は、コンピュータアーキテクチャに大きな影響を持ち、QCUに要求されるゲート操作などへも直接的に関係してきます。異なる符号への移行は、全く異なるコンピュータアーキテクチャを必要とするでしょう。

雑音を持つ物理量子ビットレイヤの特徴の中でも鍵となるのは、量子コンピュータアーキテクチャと、量子ビットやコントロールラインのレイアウトや接続性です。従来のコンピュータ設計でもあるように、モノリシックプロセッサのサイズが性能のボトルネックになることがあります。これに対する解決策はマルチコアアプローチを採用することでした。同様のボトルネックは量子ハードウェアでも生じる可能性があり、そのため、小さい量子プロセッサを接続し、大規模化を行う分散型アプローチを採用することもあり得ます。このモジューラアプローチは、離れた物理量子ビットに接続性を与えるなどの数多くの利点を持ちます（9）、（10）。そのようなモジュールは、数量子ビットを組み合わせ、全体として数千量子ビットの機能を得る、というようなことも可能にするでしょう。これは量子コンピュータデザインの選択肢の1つですが、現状ではその最適なサイズは分かっていません。

誤り耐性量子コンピュータのデザインにおいて、各々のレイヤを独立に扱うのは得策ではありません。上位レイヤの最適化は、中間の論理量子ビットレイヤで必要なリソースについて大きな影響を与え、ひいては必要とされる量子誤り訂正符号の符号長の低減につながります（8）。結果的に、これは物理量子ビットレイヤで必要とされる量子ビットやゲート操作数の減少につながります。特に、最下層における計算システムを抽象化すべきではなく、量子ビットとして使用する物理系の特性を理解することは極めて重要です。ここでの物理系の選択や制御法は、他のレイヤに多大な影響をもたらします。誤り耐性量子計算を実行するためのしきい値は、現実に量子ビットが受けるノイズの構造に強く依存します。
私たちは引き続き、量子コンピュータ構築に向け、全体像の設計のみならず、最下位から最上位レイヤまでの各々のレイヤ設計や、それらの協調設計についての研究を進めていきます。

■参考文献
（1） H. J. Kimble：“The quantum internet，”Nature, Vol. 453，pp. 1023-1030，June 2008.
（2） S. M. Brewer，J.S. Chen，A. M. Hankin，E. R. Clements，C. W. Chou，D. J. Wineland，D. B. Hume，and D. R. Leibrandt：“27Al+ Quantum-Logic Clock with a Systematic Uncertainty below 10-18，”Phys. Rev. Lett.，Vol. 123，No. 3，033201，July 2019.
（3） J. Preskill：“Quantum Computing in the NISQ era and beyond，”Quantum，Vol. 2，p. 79，August 2018.
（4） K. Nemoto，S. Devitt，and W. J. Munro：“Noise management to achieve superiority in quantum information systems，”Phil. Trans. R. Soc. A，Vol. 375，No. 2099，August 2017.
（5） F. Arute，K. Arya，R. Babbush，D. Bacon，J. C. Bardin，R. Barends，R. Biswas，S. Boixo，F. G. S. L. Brandao，D. A. Buell，B. Burkett，Y. Chen，Z. Chen，B. Chiaro，R. Collins，W. Courtney，A. Dunsworth，E. Farhi，B. Foxen，A. Fowler，C. Gidney，M. Giustina，R. Graff，K. Guerin，S. Habegger，M. P. Harrigan，M. J. Hartmann，A．Ho，M. Hoffmann，T. Huang，T. S. Humble，S. V. Isakov，E. Jeffrey，Z. Jiang，D. Kafri，K. Kechedzhi，J. Kelly，P. V. Klimov，S. Knysh，A. Korotkov，F. Kostritsa，D. Landhuis，M. Lindmark，E. Lucero，D. Lyakh，S. Mandrà，J. R. McClean，M. McEwen，A. Megrant，X. Mi，K. Michielsen，M. Mohseni，J. Mutus，O. Naaman，M. Neeley，C. Neill，M. Yuezhen Niu，E. Ostby，A. Petukhov，J. C. Platt，C. Quintana，E. G. Rieffel，P. Roushan，N. C. Rubin，D. Sank，K. J. Satzinger，V. Smelyanskiy，K. J. Sung，M. D. Trevithick，A. Vainsencher，B．Villalonga，T．White，Z. J. Yao，P. Yeh，A. Zalcman，H. Neven，and J. M. Martinis：“Quantum supremacy using a programmable superconducting processor，”Nature，Vol. 574，pp. 505-510，Oct. 2019
（6） H. S. Zhong，H. Wang，Y. H. Deng，M. C. Chen，L. C. Peng，Y. H. Luo，J. Qin，D. Wu，X. Ding，Y. Hu，P. Hu，X. Y. Yang，W. J. Zhang，H. Li，Y. Li，X. Jiang，L. Gan，G. Yang，L. You，Z. Wang，L. Li，N. L. Liu，C. Y. Lu，and J. W. Pan：“Quantum computational advantage using photons，”Science，Vol．370，No．6523，pp. 1460-1463，Dec. 2020.
（7） https://ai.googleblog.com/2018/03/a-preview-of-bristlecone-googles-new.html
（8） M. Hanks，M. P. Estarellas，W. J. Munro，and K. Nemoto：“Effective compression of quantum braided circuits aided by ZX-Calculus，”Phys. Rev. X，Vol. 10，No. 4，041030，Dec. 2020.
（9） K. Azuma，H. Takeda，M．Koashi，and N. Imoto：“Quantum repeaters and computation by a single module: Remote nondestructive parity measurement，”Phys. Rev. A，Vol. 85, No. 6, 062309，June 2012.
（10） K. Nemoto，M. Trupke，S. J. Devitt，A. M. Stephens，B. Scharfenberger，K. Buczak，T. Nöbauer，M. S. Everitt，J. Schmiedmayer, and W. J. Munro：“Photonic Architecture for Scalable Quantum Information Processing in Diamond，”Phys. Rev. X, Vol. 4, No. 3, 031022，August 2014.