量子コンピュータや量子ネットワークの可能性が近年注目されつつありますが、その実現のためにもっとも必須となる技術が誤り耐性技術です。量子情報処理と既存の情報処理（古典情報処理）で起き得るノイズ量には莫大な差があります。古典情報処理ではエラーが起きる頻度が小さいため、多くの情報処理はそれほどエラーを気にせず処理可能でした。しかし、量子情報処理ではエラーが起きる頻度が非常に大きいため、エラー対策なしで行える計算は小さな規模のものでしかないことが分かっています。量子情報処理をスケーラブルにし、有用なさまざまな計算を行い、大きなネットワークとしていくためには、量子情報の誤り耐性処理を行い、量子情報をノイズから強固に保護をする必要性があります。このため、量子情報処理においては、誤り耐性処理がコンピューティング技術およびネットワーク技術アーキテクチャの根幹部分となると予想されます。NTTセキュアプラットフォーム研究所では、この量子情報をエラーやノイズから守る誤り耐性技術を重要な基盤技術として研究を進めています。量子情報処理のための誤り対処法としては大きく分けて2つの手法があります。それは量子誤り訂正符号と量子誤り抑制（ノイズ補償）手法です。量子誤り訂正符号は、量子ビットを冗長に符号化することによって、一部にエラーが起きても復号をすることで訂正が可能な手法です。これはスケーラブルに誤り耐性処理が可能であることがこれまでに分かっている唯一の手法であり、将来的な規模の大きな量子情報処理の実用化のために必須な技術であると予想されます。しかし、符号化のために必要な量子ビット数や処理数の増加が避けられず、これによる誤り耐性処理の実現は少し先になると考えられています。では、それまで何も打つ手がないのかというとそうではなく、もう1つの技術として注目されているのが量子誤り抑制（ノイズ補償）手法です。これは量子ビット数のオーバヘッドなしに正しい計算結果を予測することで、計算結果から誤りを取り除こうという技術です。誤りのない計算結果の予測のために計算処理のコストは増加し、スケーラブルとはなりませんが、量子ビット数のオーバヘッドがいらないため、まだ量子情報処理の規模が小さいうちに重要な技術とされています。一方で、実装する要素技術そのものができる限り精度が高いこと、ネットワーク処理や分散処理に向けての機能が高いことも重要です。本稿では、量子誤り訂正符号を用いた誤り耐性量子計算に向けたソフトウェア基盤の研究開発、量子誤り抑制（ノイズ補償）手法の技術、および実装するための要素技術について紹介します。

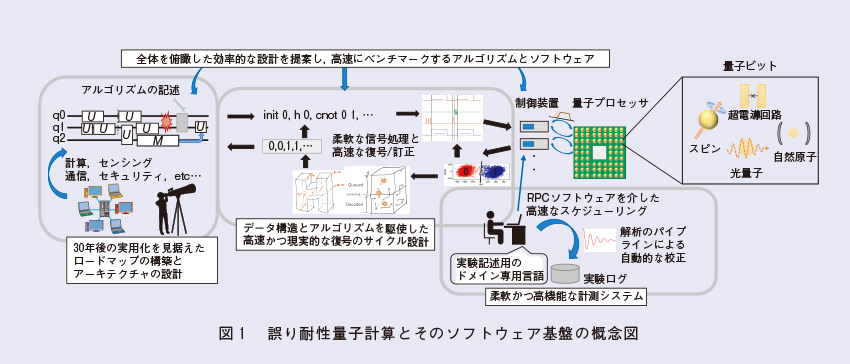
量子コンピュータは物質の重ね合わせ状態を利用しさまざまな情報処理を可能にしますが、その代償としてノイズに対して脆弱で、単位命令のスループットが遅いという欠点を持ちます。既存の計算機のメモリ、例えばDRAM（Dynamic Random Access Mem­ory）ではキャパシタの充電・放電で0、1を表し、十分なマージンを設けたしきい値動作のもと、自然放電で情報が失われるより早くリフレッシュを行うことで、小さなオーバヘッドで情報の長期保存を実現しています。これに比べ、同じく電子を操る超伝導回路を用いた量子ビットは、ビット反転といった単位操作が低速なだけでなく、量子力学の性質の1つであるクローン禁止定理などから直接的なリフレッシュが行えません。この問題は量子誤り訂正符号を用いて量子ビットを符号化し、エラーを間接的に検出し訂正し続けることで回避できますが、量子誤り訂正を行った状態で計算を行うには誤り訂正をしない場合に比べ、時間、サイズともに数百倍や数千倍といった莫大なリソースが必要となります（1）。このように、量子コンピュータは「揮発性メモリから揮発する情報をリフレッシュの代わりに誤り訂正符号と高速なフィードバックで抑え込む」ような複雑な計算機アーキテクチャになることを宿命付けられています。したがって、実用的な誤り耐性量子コンピュータを実現するには、優れた量子デバイスの開発に加え、容易な拡張性、広帯域なインタフェース、安価でロバストな制御などを満たすシステムの構築が必須となります。私たちのグループは、実用的な誤り耐性量子コンピュータを実現するべく、理化学研究所や大学と共同で高い性能と信頼性を両立する超伝導量子コンピュータの研究開発を行っています。ここでは、私たちが重点的に取り組んでいる量子コンピュータのソフトウェア基盤について3つのトピックを紹介します（図1）。
１番目は、チップ上の多数の超伝導量子ビットを効率的に特徴付けし、校正を行うシステムです。現状の超伝導量子ビットは性能のばらつきから個別制御が必須であり、計算機は大量のFPGA（Field Programmable Gate Array）やマイクロ波源などからなる巨大な分散システムとなっています。私たちはこうした機器を非同期に制御し、大量の量子ビットを自動かつ高速に校正するためのライブラリを構築し、機械学習や量子的なランダム性を活用した効率的な特徴付けや校正の手法を提案しています（2）、（3）。
2番目は、量子誤り訂正での復号に必要な演算やフィードバックを行う周辺回路の設計です。量子誤り訂正で用いられるトポロジカル誤り訂正符号でのエラーの最尤推定は、最小重み完全マッチングと呼ばれるグラフの問題に帰着できますが、この問題の素朴な解法はレイテンシが大きく実用的でないため、データ構造や計算機アーキテクチャを工夫し速度を改善する必要があります。私たちのグループは、小規模な符号の復号回路を機械学習で最適化する手法（4）や、単一磁束量子を用いた高速な復号手法の提案（5）に取り組んでいます。
3番目は、前述のような提案を評価するためのプログラムを、技術レイヤをまたいで翻訳する処理系とこれをシミュレートするソフトウェア群の構築です。特に、量子回路のシミュレータは緻密な高速化によっていくつかのベンチマークで世界最高速を実現しています（6）。前述のように、誤り耐性量子コンピュータの大規模化は、大規模な分散システムを駆使し、最適化された制御デバイスとアルゴリズムで高い実効性能と信頼性を確保しつつ、いかに集積化された量子デバイスを制御するかという戦いであり、こうした技術を研鑽してきたNTT研究所に適した挑戦的課題といえます。

2019年10月、量子コンピュータが古典コンピュータで解くのに１万年かかるといわれた問題を53量子ビットの小規模な量子デバイスを用いて200秒で解くことができたとGoogle が発表しました（7）。この実証実験で使われたような小規模でノイジーな量子コンピュータは、NISQ（Noisy Intermediate-Scale Quantum）コンピュータと呼ばれています。Google が解いた問題は、１万年ではなくスーパーコンピュータを用いて数日で解くことができるという反論もありますが、量子コンピュータのサイズが大きくなるにしたがって、この差はさらに広まっていくと考えられています。このような小規模量子デバイスをどのように実用上役立てれば良いかと世界中の研究者が研究しており、主に化学計算や機械学習への応用が期待されています。
一方、このような小規模量子コンピュータの計算エラーは無視ができません。歴史的にエラーを抑える手法として量子エラー“訂正”が研究されてきました。量子エラー訂正では、１論理量子ビットを表すのに複数の量子ビットで符号化しエラー訂正を行うことで、符号化に用いた量子ビット数に対して指数関数的にエラーを抑えることができますが、量子ビット数が限られているNISQ コンピュータには不向きです。そこで、ハードウェア側の負担を大きくすることなくエラーを抑える量子エラー“抑制”の研究がさかんに行われています（8）。量子エラー抑制は量子ビット数を増やす必要はありませんが、より多くの測定回数が必要となります。
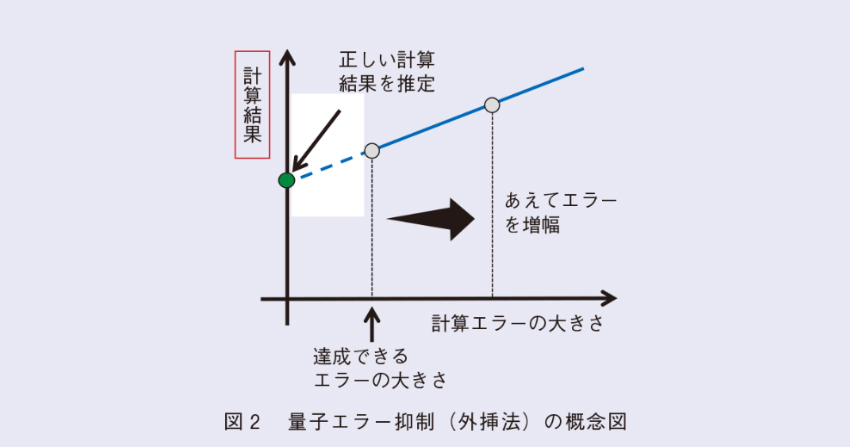
近年さまざまなエラー抑制法が提案されています。ここでは、まず、もっともシンプルで分かりやすい外挿法を説明します。量子コンピュータの計算エラーはノイジーな操作を加えることなどにより、あえて増やすことはできます、そこで、もともとの結果と、計算エラーを増やした後の結果を外挿することによって、計算エラーのない計算結果を推定できるのが外挿法です。外挿法の概念図を図2に示します。また、計算エラーのエラーモデルを同定し、そのエラーの逆変換をほどこして実効的にエラーをキャンセルする擬似確率法と呼ばれる手法も存在します（9）。ほかには、対称性検証法、部分空間展開法などといった手法があります。詳細は筆者が執筆したレビュー論文（8）を参照してください。
さらに、私たちのグループはこれから量子ビット数が増えていくと見越して、量子誤り訂正を用いた誤り耐性量子計算がある程度可能になった後も、さらに計算精度を向上するために量子エラー抑制が有用であるということを世界で初めて示し（10）、量子エラー訂正と量子エラー抑制は別々に考えるべきものではなく、統合したスキームとして考えるべきであることを示しました。

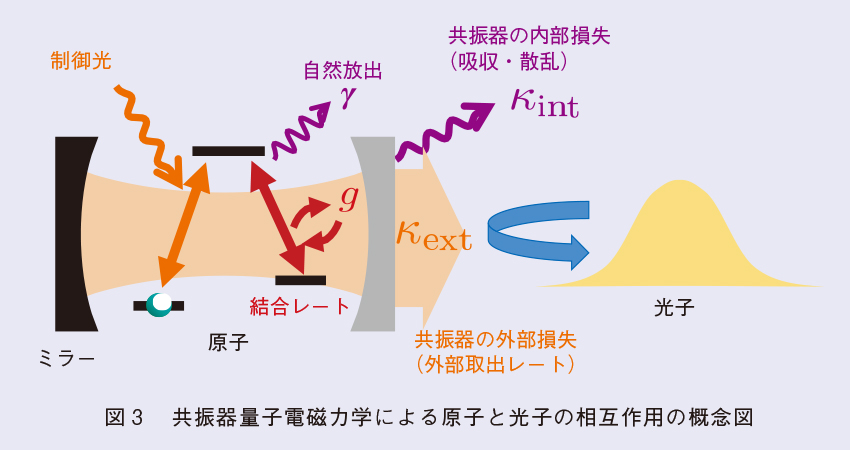
これまでは与えられた実装方式のうえで、誤り耐性処理をソフトウェア的にいかに効果的に行うかという取り組みを紹介してきました。一方で、要素技術の実装方式そのものが精度高く動作すること、実装の規模が大きくなること、ネットワーク化、分散処理などその機能が高度になっていくことも、誤り耐性を強くするうえで重要な技術です。特にネットワークを含めた機能を拡大するために重要な技術が、共振器量子電磁力学（共振器QED）を用いた原子と光子の相互作用（図3）によるさまざまな要素技術であり、NTTセキュアプラットフォーム研究所では、量子中継などを含めた将来的な量子セキュアネットワーク基盤のためにこの実装方式について研究を行っています。
まず、通信のためには通信用の量子ビットとなる光子を高効率で生成する必要があります。レーザの微弱光による代用や非線形結晶を用いた生成では単一光子としての精度や効率に問題点がありますが、共振器QEDを用いた場合は、精度の高い単一光子生成が高効率に可能となります（11）。さらにパルス長を短くしていくことで繰り返しレートの向上も図り、情報処理としての総合的な性能が向上するよう検討を進めています（12）。また、原子を量子ビットメモリとし、光子を通信用の量子ビットとした場合に、共振器QEDを用いると原子と光子の間で精度の高い量子ゲートが可能となります。これについては光子の損失とゲートの忠実度の面で誤り耐性にトレードオフが起こることを考慮し、誤り耐性が最適となる実装方式を検討しています（13）。また、超伝導量子コンピュータを分散処理するためには超伝導量子ビットと同じ周波数領域であるマイクロ波の光子との量子ゲートやルーチングなどを行う必要があります、これらを効率的に行う回路量子電磁力学（回路QED）を用いた技術についても研究を行っています（14）、（15）。

私たちは量子情報処理の誤り耐性処理に向けて、ソフトウェア的にいかに効率的に優れた誤り耐性処理を行うかという観点から、誤り耐性量子計算のソフトウェア基盤の研究開発および量子誤り抑制手法の研究を行っています。また、物理実装の要素技術自体の精度や効率を良くし、いかに機能を拡大するかという逆の面からの研究開発にも取り組んでいます。最終的に、十分規模の大きな誤り耐性量子コンピュータの実現はまだ遠い将来だと予想されていますが、それに向けて効率的な新たなアーキテクチャを生み出すことをめざしています。また、それまでの過程においても量子誤り抑制などを活用し、なるべく近い将来から可能な限り有意義な量子情報処理を行えるよう新たな研究に取り組んでいます。

■参考文献
（1） A. G. Fowler and C. Gidney:“Low overhead quantum computation using lattice surgery,”arXiv: 1808.06709, 2018.
（2） K. Heya, Y. Suzuki, Y. Nakamura, and K. Fujii:“Variational Quantum Gate Optimization，”arXiv: 1810.12745, 2018.
（3） Y. Nakata, D. Zhao, T. Okuda, E. Bannai, Y. Suzuki, S. Tamiya, K. Heya, Z. Yan, S. Tamate, and Y. Tabuchi:“Constructing Exact Unitary t-designs by Quantum Circuit and Applications to Higher-Order Randomized Bench­mar­king,”2021.
（4） A. Davaasuren, Y. Suzuki, K. Fujii, and M. Koashi:“General framework for constructing fast and near-optimal machine-learning-based decoder of the topological stabilizer codes，”Phys. Rev. Research, Vol. 2, No. 3, 033399, 2020.
（5） Y. Ueno, M. Kondo, M. Tanaka, Y. Suzuki, and Y. Tabuchi: “Quantum Error Correction with a Superconducting De­cod­er，”QCCC 2020, Dec. 2020.
（6） Y. Suzuki, Y. Kawase, Y. Masumura, Y. Hiraga, M. Nakadai, J. Chen, K. M. Nakanishi, K. Mitarai, R. Imai, S. Tamiya, T. Yamamoto, T. Yan, T. Kawakubo, Y. O. Nakagawa, Y. Ibe, Y. Zhang, H. Yamashita, H. Yoshimura, A. Hayashi，and K. Fujii:“Qulacs: a fast and versatile quantum circuit simula­tor for research purpose，”arXiv: 2011.13524, 2020.
（7） F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Yuezhen Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Marti­nis:“Quantum supremacy using a programmable supercon­duct­ing processor,”Nature, Vol. 574, pp. 505-510, Oct. 2019.
（8） S. Endo, Z. Cai, S. C. Benjamin, and X. Yuan, “Hybrid quantum-classical algorithms and quantum error mitiga­tion,”J. Phys. Soc. Jpn., Vol. 90, 032001, 2021.
（9） S. Endo, S. C. Benjamin, and Y. Li:“Practical Quantum Error Mitigation for Near-Future Applications,”Phys. Rev. X, Vol. 8, No. 3, 031027, 2018.
（10） Y. Suzuki, S. Endo, K. Fujii, and Y. Tokunaga:“Quantum error mitigation for fault-tolerant quantum comput­ing,”arXiv: 2010.03887, 2020.
（11） H. Goto, S. Mizukami, Y. Tokunaga, and T. Aoki:“Figure of merit for single-photon generation based on cavity quantum electrodynamics,”Phys. Rev. A, Vol. 99, No. 5, 053843, May 2019.
（12） Y. Tokunaga, H. Goto, T. Utsugi, and T. Aoki:“Figure of merit for the efficiency of single photon generation using cavity- QED systems,”International symposium on single photon based quantum technologies, 2019.
（13） R. Asaoka, Y. Tokunaga, R. Kanamoto, H. Goto, K. Koshino, and T. Aoki:“Suitable fault-tolerant schemes for cavity-QED-based quantum computation,”CLEO Pacific Rim conference, 2020.
（14） K. Koshino, K. Inomata, Z. R. Lin, Y. Tokunaga, T. Yamamoto, and Y. Nakamura:“Theory of Deterministic Entanglement Generation between Remote Superconducting Atoms,”Phys. Rev. Applied., Vol. 7, No. 6, 064006, June 2017.
（15） S. Masuda, S. Kono, K. Suzuki, Y. Tokunaga, Y. Nakamura, and K. Koshino:“Nonreciprocal microwave transmission based on Gebhard-Ruckenstein hopping,”Phys. Rev. A, Vol. 99, No. 1, 013816, Jan. 2019.