ネットワークやグラフを含む関係データを二次元配列（行列）として表し、その関係データから互いに類似するデータが集まっている長方形の領域（長方形クラスタ）に分割することは、データ解析の基本的な手法の１つです。
本成果では、任意のサイズのデータに対する長方形分割クラスタリングにおいて、あらゆる組合せ候補を生成できる新しい確率的生成モデル（確率的無限長方形分割モデル）を考案し、これを用いることで、長方形クラスタの分割数やそれぞれの大きさなどのモデルパラメータを、従来よりも分割パターンに関する制約が少なく、かつ実現可能な時間内で、データ駆動的に最適化できる機械学習技術を実現しました。
従来、関係データからのデータ駆動型の長方形分割クラスタリング手法の多くでは、解析の結果得られる組合せ候補に何らかの制約を設ける必要がありました。例えば、候補を生成する際に、サイズの不規則な碁盤の目のように、格子状の領域に限って分割する手法（regular grid partitioning）（1）や、データを大きなサイズの長方形に分割したのちに段階的に小さなサイズの長方形に分割するような手法（階層的分割：hierarchical partitioning）（2）が提案されています。しかし、これらの手法では、生成できない組合せ候補が存在します。
一方、提案する手法では、あらゆる長方形分割の候補を生成できることが理論的に保証されています。私たちは同等の能力を持った解析技術を2014年にも提案しました（3）が、実装が非常に複雑で、多くの計算時間が必要でした。今回の手法では、2014年の手法と比較して実装が大幅に簡単になり、ベンチマークデータ課題に対する計算速度は2014年の手法を大きく上回ることが実験的に確認されています。例えば、入力データの要素数が250,000のとき、提案手法では2014年の手法に対し、同等の予測精度に達する計算時間が約半分に短縮されました。
この手法は、入力データに対して、あらゆる長方形分割クラスタリングの候補をベイズ推論することによって解析結果を得ることができます。したがって、この手法を用いたデータ解析では、事前にモデルやパラメータに特定の条件を与える必要がありません。このような事前の知識・条件設定が不要である提案手法は、AIが人間の脳のように、さまざまな状況に合わせて自律的に適応する、自律的AIモデルを実現する可能性を大きく広げたといえます。

本成果のポイントは、二次元配列（行列）の長方形分割に対して、任意のサイズの行列に対してあらゆる長方形の組合せ候補を生成できる、新しい確率的生成モデルを発見したことにあります。その確率的生成モデルの構成にあたっては、組合せ論の世界で発見された長方形分割の重要な性質を利用しています。
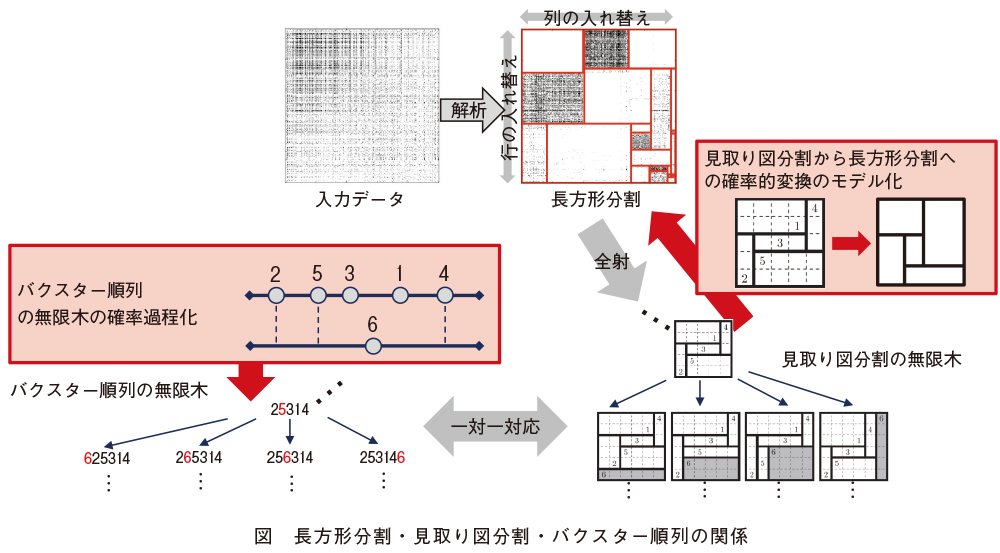
入力データにふさわしい長方形分割を見つける問題は、一見すると図形の操作を扱う幾何学的な問題のようにとらえられますが、以下の手続きによって数字列の操作を扱う代数的な問題にすり替えることができます。長方形分割（図上）において、各長方形クラスタのサイズを不問とすると、それは見取り図分割（図右下）とみなすことができます。いかなる長方形分割も、ありとあらゆる見取り図分割の中のいずれか1つに対応することが知られています（長方形分割から見取り図分割への全射が存在します）。この見取り図分割の各長方形クラスタに対して特別な手順によって数字を割り当てると、各見取り図分割に対して一意に定まるバクスター順列（図左下）（4）と呼ばれる特別な数字列を一対一に対応させることができます。結果として、ありとあらゆる長方形分割の候補から所望のものを見つける問題は、ありとあらゆるバクスター順列の中から所望のバクスター順列と、各長方形クラスタのサイズという2種類のパラメータを表す数字列を見つけ出す問題に置き換えることができるようになりました。
本成果では、この問題に対して確率的生成モデルを用いた統計的機械学習手法によって解決する手段を提案しました。前述の長方形分割、見取り図分割、バクスター順列の間の関係を利用して、データ解析へ適用可能な長方形分割の確率的生成モデルを構成しました。私たちはまず、あらゆるバクスター順列を過不足なく取りつくすことのできるような確率的生成モデル（図左下）を構成し、次にバクスター順列に対応する見取り図分割から長方形分割へ変換するための確率的なアルゴリズム（図右下）を構成しました。結果として、任意のサイズのデータに対する長方形分割クラスタリングにおいて、本成果において提案する確率的生成モデルが、あらゆる組合せ候補を生成できることを理論的に保証できました。この確率的生成モデルは、モデル自身の構造やパラメータをデータ駆動的に調整して、入力された関係データを最適にクラスタリングできます。

関係データに対するデータ駆動型の解析技術は、近い将来、さまざまな機械学習・人工知能技術へ積極的に導入されていくことが期待されます。例えば、ソーシャルネットワーキングサービスから得られる複雑で大量のデータの解析において、エンジニアによる学習モデルの高度な調整を補助するような活用が考えられます。また、ニューラルネットワーク深層学習における学習済みネットワークからの知識獲得や、データ・アプリケーションに最適なネットワーク構造の設計を補助する場面での利用可能性もあります。

■参考文献
（1） C. Kemp, J. B. Tenenbaum, T. L. Griffiths, T. Yamada, and N. Ueda :“Learning systems of concepts with an infinite relational model,” Proc. of AAAI Conference on Artificial Intelligence,pp. 381-388, 2006.
（2） D. M. Roy and Y. W. Teh :“The Mondrian process,” Proc. of Advances in Neural Information Processing Systems, 2009.
（3） M. Nakano, K. Ishiguro, A. Kimura, T. Yamada, and N. Ueda　:“Rectangular tiling process,”Proc. of International Conference on Machine learning,pp. 361-369,2014.
（4） G. Baxter :“On fixed points of the composite of commuting functions,”Proc. of American Mathematical Society, Vol. 15,pp. 851-855,1964.

中野　允裕
NTTコミュニケーション科学基礎研究所
メディア情報部　メディア認識研究グループ

私が子どものころに読んだサイエンス・フィクションにおける近未来では、しばしば人工知能が人間と共存・自律して生活している様が描かれていました。現在の機械学習・人工知能技術の発展は、まさに子どものころに夢見たような自律的人工知能が実現される未来を予感させてくれます。実際、近年では、膨大なデータを大規模なパラメータを通して学習したモデルの中に、特定の課題においては人間よりも高い性能を示すようなものまで登場しつつあります。
私は子どものころに見たサイエンス・フィクションの世界に登場するような人工知能の実現を夢見て、自律的に環境に適用しながら未来永劫破綻することなく学習を続けられることの保証された機械学習技術の理論・応用の研究に従事しています。多様な環境への適応とは、計算機によっては無限に多くの観測データを与えられるような状況に似ています。それに伴って、モデルの表現に必要なパラメータも際限なく大きくなっていくかもしれません。それでは、データ・モデルが再現なく大きくなっていったとき、果たして人工知能はそれに伴って正しく自身のモデル学習を行っていくことはできるのでしょうか。このように、データ・モデル規模が無限に大きくなったときにもモデル学習が正常に機能するか否かを問う問題は、技術的に非常に難しい問題を含んでいます。私の研究の目標は、無限の彼方で正常に機能する機械学習モデルを実装し、未来永劫自律的に環境に適用し続けることのできるような人工知能を実現することです。