耐量子計算機暗号とは「高性能な量子コンピュータの攻撃に対して安全性を保つことができる暗号」のことです。近年では、量子コンピュータの研究開発が急速に進んできており、近い将来に量子コンピュータが一般に普及する可能性があります。現在の暗号方式は素因数分解の難しさに安全性の根拠を置いているのですが、量子コンピュータでは従来の古典コンピュータには不可能であった素因数分解が可能であるという特徴があります。そのような量子コンピュータが一般に普及した場合、暗号が数分で解読され、社会的混乱が起きると予測されています。そのため、汎用量子コンピュータが実現する前に、実用上の暗号をすべて耐量子計算機暗号に置き換える準備を行い、未来の安心・安全な情報通信を実現することが求められています。実際に、米国立標準技術研究所（NIST）では、2017年から耐量子計算機暗号の標準化計画に乗り出しており、量子コンピューティングに抵抗できる情報セキュリティシステムの需要はかなり高まっているため、私もNTTで耐量子計算機暗号の研究を始めました。
私が入社後最初に取り組んだのは、耐量子安全な公開鍵暗号の研究です。「そもそも暗号とはどういったものか」を表す例として、公開鍵暗号方式における南京錠の例がよく知られています。南京錠は誰でも箱（データ）にロック（暗号）をかけられるのですが、それを開けるためには鍵（暗号解読）が必要になります。そこで箱（データ）を送る際には南京錠を用意し、ロック（暗号）をかけた箱にデータを入れて送ることで安全な通信ができるようになります。これが公開鍵暗号と呼ばれる暗号です。具体的に私の研究では、弱い安全性（CPA安全性）を持つ暗号方式を変形して、強い安全性（CCA安全性）を持つものにするための、汎用的な手法を提案していました。この手法はその後NTRUという鍵交換・公開鍵暗号方式において採用され、NISTによる、耐量子計算機暗号の標準化コンペティションにおいて、最終候補まで残りました。

耐量子計算機暗号分野の中で、特に私が研究を進めているのが「ゼロ知識証明」と「秘密計算」の研究です。「ゼロ知識証明」とは、簡単に説明すると「ある命題が正しいことを、その正しさ以上の知識を与えることなく証明する」ことを実現する暗号プロトコル（暗号を使った通信手順）です。これは例えば、「あるパズルにきちんと答えが存在することを証明したい」とします。答えをそのまま開示すれば「答えが存在すること」の証明になりますが、これでは答えという「知識」を与えてしまうことになります。そこでパズルに答えがあることの「知識」を教えることなく、証明することを可能にする技術がゼロ知識証明です。
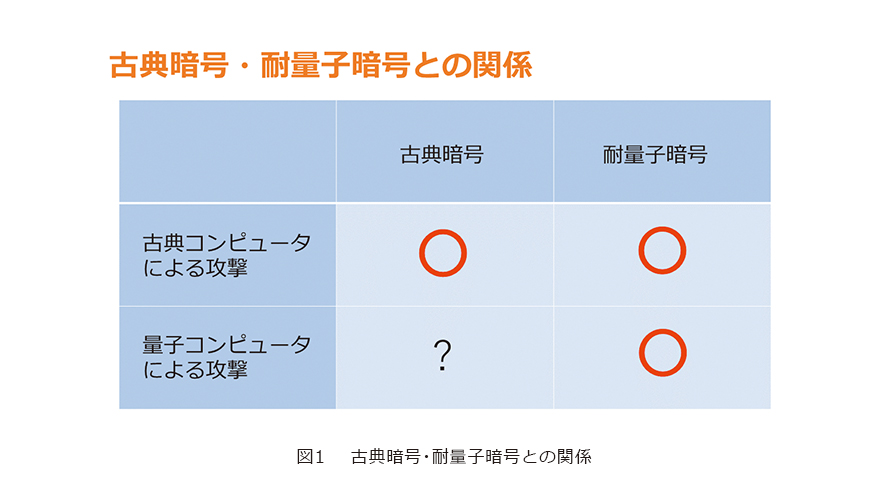
従来の暗号理論では、基本的にゼロ知識証明の安全性において古典コンピュータを用いる攻撃者しか考慮しておらず、攻撃者が量子コンピュータを用いた場合に安全になるかが不明であったため、ゼロ知識証明の耐量子安全性の研究に取り組んでいます（図1）。現在研究を進める中で、否定的結果と肯定的結果の2つの結果を得ています。否定的結果としては、この古典安全な方式と同等の良い性質を満たす、耐量子安全なゼロ知識証明の方式は「存在しない」ことを証明しました。これは古典安全なゼロ知識証明と耐量子安全なゼロ知識証明の本質的な差を示すものであり、驚くべき結果です。肯定的結果としては、ゼロ知識性の定義を実用上問題ない範囲でわずかに緩和すれば、上記古典安全な方式の適切な変形がそのまま耐量子安全になることも証明しました。この研究の応用例としては「自身の身分を明かすことなく正当な身分証を持っていること」を証明する等の匿名認証プロトコルへの応用があります。
そして「秘密計算」とは、複数の人がそれぞれ持っているデータ自体を開示することなく、例えばそれらのデータの何らかの統計量を計算するための暗号プロトコルです。従来の研究ではゼロ知識証明と同様に、基本的に古典攻撃者のみが考えられており、耐量子安全性は不明でしたのでその研究に取り組んできました。具体的な研究内容としては、通信を行う二者間において、古典安全な方式と同等の良い性質を満たす耐量子安全と、わずかな緩和版安全性を持つ方式を構成しました。

その他の取り組みとして「量子計算機を用いて新たな暗号機能を創出する研究」を行っています。従来の古典暗号プロトコルには、すべてがデジタルデータで表されることに起因する不可避な問題があります。例えばあるデータを一度手に入れれば、それはいくらでもコピーでき、またそのデータを削除したことを別の人の立場から確認する術はありません。しかし一方で現実的な要求としては、あるデータのコピーを防止したり、データが削除されたことを保証したりするという、通信における社会的な要求が多くありました。そこでこのような機能を暗号学的手法で実現するために、量子計算機を用いた暗号プロトコルの研究を行っています（図2）。
具体的な研究内容としては、量子力学における「複製不可能定理」という、与えられた量子状態を複製することは不可能であるという定理を上手く活用することで、実現したい暗号機能を実現します。これはいくらでもコピーが可能な古典的デジタルデータとは本質的に異なるため、これを利用して暗号文を削除したことを証明できるような暗号方式の研究を行いました。また安全にソフトウェアを貸し出すため、暗号プロトコルの研究を行っています。これはつまり、ソフトウェアを貸し出している間はそのソフトウェアを実行できるのですが、それを返却した後は実行できないというような機能を実現するものです。このようなプロトコルはすでに提案されていましたが、研究を行いより信頼性の高い安全性を持つ機能を実現することに成功しました。
これらの量子計算機を用いた新たな暗号機能については、新たな技術であるため、まだこれから基礎理論が成熟していくという段階です。現時点では概念実証の段階ですが、コピー不可能なプログラムやデータの削除証明等の社会的需要もあると考えられており、将来的に現実世界で有用な応用はこれから多く出てくると思います。
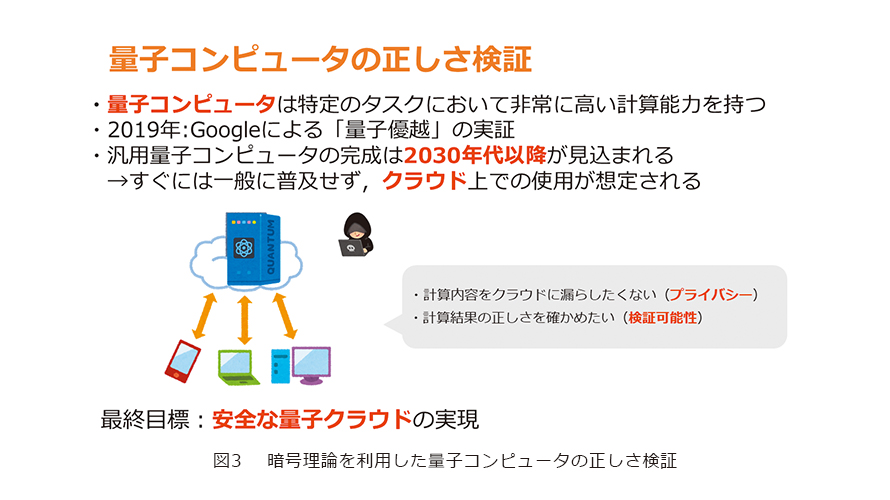
また暗号理論を利用して、量子計算機の検証の研究も行っています。量子計算機は現在急速に開発が進んできていますが、一般に普及するまではかなり時間がかかるため、それまでに一般のユーザが量子コンピュータを使うためには、古典コンピュータからクラウドを通じて量子コンピュータを用いると考えられています。その際にクラウドが正しい計算結果を返してくれていることを保証するため、量子計算の正しさを検証する必要があります。研究内容のイメージとしては、正しく計算したときのみに正しい答えが出るような「パズル」を量子コンピュータに解かせます。このパズルはユーザ側が生成するためユーザは答えを知っており、量子コンピュータがもし正しい答えを出した場合、ユーザは計算結果が正しいと確認できます。反対に、もし答えが正しくなかった場合、量子コンピュータは正しく計算しなかったということが分かります。実際にはこれを実現するために、上手く暗号学的なツールを量子計算に埋め込むことにより実現します。
また、その前の量子コンピュータの研究開発段階においても「本当に正しく動作する量子コンピュータをつくることができているのか」ということを検証する必要があります。この研究の進捗としては、量子計算の正しさの検証を非常に高速に行う方法を提案しました（図3）。また、「量子計算機を持っていること」の検証を行うプロトコルで、暗号学的な道具としてハッシュ関数と呼ばれるランダムにふるまう関数だけを用いるという、従来とは根本的に異なる全く新しい方法を提案しました。

古典暗号理論は長年の積み重ねにより基礎的な結果が整備されている一方で、私の研究している量子暗号理論は始まって間もない研究のため、まだ全くの未整備状態であり、非常に基礎的な部分において未解決問題が多く存在します。一例を挙げれば、古典暗号理論における多くの暗号機能は「計算が容易にできる一方で計算結果から元の入力を求めることが困難」という性質を持つ、一方向性関数の存在と等価であることが分かっていますが、量子暗号理論においては同様の結果はまだ知られていません。最近では2019年に大手IT企業が、量子コンピュータが古典コンピュータよりも速く問題を解決できること（量子優位性）を主張する論文を発表したのですが、この方法は暗号理論的な意味で「検証可能」ではなく、本当に古典計算機を超えたということを第三者の立場で確信できるものではありませんでした。一般論としても、基礎的な理論の欠如が、より複雑・高機能な暗号の構成において障害になる場合があります。そのためまずは、暗号理論的な方法で量子優位性を検証する方法の研究を推し進めて、基礎的な問題を解決することが課題です。

私が研究を行ううえで大切にしている信条は、「世界中の研究者を驚かせられるような、極めて難しいと考えられている問題を解決すること」です。確かに難しい問題を解こうとする中で、試みの多くは失敗に終わります。しかし高い目標を掲げることによって、副産物的にさまざまな面白い研究成果が得られることも多くあるため、高い目標を掲げて研究に臨むことは非常に大切であると感じています。これからの研究の目標としては、直近での応用をめざすのではなく「基礎的な理論の研究を通じて将来の研究開発に貢献したい」という思いがあります。具体的には、量子暗号理論における基本的な未解決問題を解決することで、数十年後・数百年後にも残る成果を挙げたいです。そしてこれらの研究成果により、人類の「計算」に対する理解が深まれば、より量子計算機を利活用した、より豊かな社会が実現できると信じています。

暗号理論の世界では、NTTの名前は世界的に知られていて、国際会議等でNTTといえばまず伝わるので、名刺代わりになるというメリットがあります。また世界中から招聘教授や優秀なポスドク・インターン生等が集まり、国際的な人脈が形成できるというのは、研究を進めていく中でどのような分野においてもとても大きなアドバンテージです。私の所属しているNTT社会情報研究所の阿部特別研究室では、特に暗号理論の基礎的な研究に特化していますが、このように基礎理論研究の重要性を認識し、研究を続けさせていただいていることはありがたいですし、世界的にも数少ない優れた研究機関の1つであると思います。そしてそうした基礎研究こそが、将来のNTTの競争力の源泉にもなると信じて、これから日々研究を続けていきます。
最後に、いつも研究と議論にお付き合いただいている、共同研究者の皆様にお礼申し上げます。日々、さまざまな方々との議論を通じて、新たなアイデアが生まれていると思っています。これからも、ご興味がある方はぜひ一緒に研究を進めていければと思います。