2024年7月号
特集
多様な数学が交差する複素力学系の世界──非アルキメデス的力学系の視点から
- 力学系
- カオス
- 非アルキメデス的数
複素力学系は純粋数学の一領域です。力学系理論という解析的な領域でありながら、代数学や幾何学などを含めた純粋数学における幅広い分野とのつながりの中で研究が進められてきました。特に筆者はこの複素力学系を、整数論という全く異なる分野で生み出された非アルキメデス的数と呼ばれる数の理論を用いて研究しています。本稿ではこれらの研究の概要とその魅力を紹介します。
色川 怜未(いろかわ れいみ)
NTT基礎数学研究センタ
複素力学系とその展開
複素力学系とは複素係数の漸化式が定める離散力学系の漸近挙動を調べる分野です。例えば漸化式 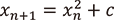 (
(  は複素数)の
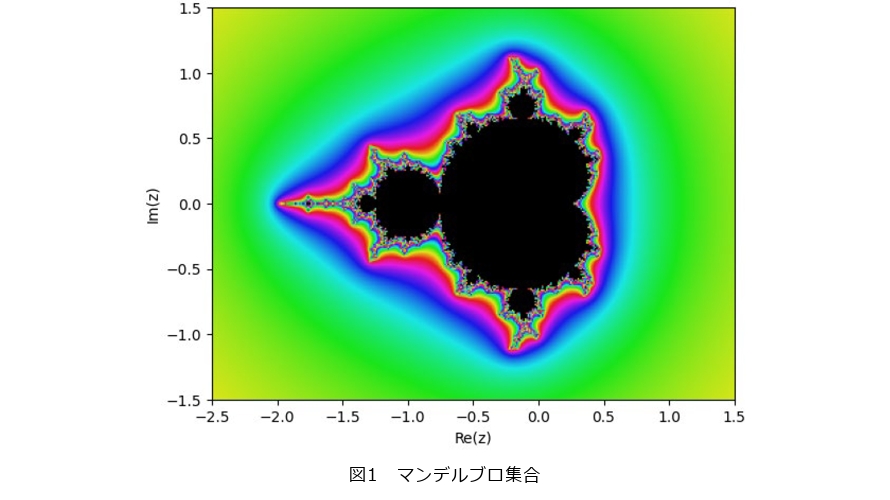
は複素数)の  での挙動は、漸化式自体の見た目の単純さとは裏腹にマンデルブロ集合(図1)に代表される複雑で豊かな構造と密接にかかわっています。近年は特に空間やパラメータの次元を増やした高次元の力学系に関する研究が盛んです。それらの研究で興味深いことは、実力学系や数論的力学系、非アルキメデス的力学系、代数幾何学、アラケロフ幾何学などの他の研究分野とのかかわりの中で研究が進められている、ということでしょう。これらの分野はそれぞれ研究対象も手法も大きく異なりますが、ある分野が進展することで複素力学系に関する研究が大きく進展したり、逆に複素力学系の研究成果を用いて他分野の研究がなされたりしています。本稿では複素力学系という分野の大まかな紹介の後に、例として筆者の専門である非アルキメデス的力学系について、その概説と複素力学系との関係を紹介します。
での挙動は、漸化式自体の見た目の単純さとは裏腹にマンデルブロ集合(図1)に代表される複雑で豊かな構造と密接にかかわっています。近年は特に空間やパラメータの次元を増やした高次元の力学系に関する研究が盛んです。それらの研究で興味深いことは、実力学系や数論的力学系、非アルキメデス的力学系、代数幾何学、アラケロフ幾何学などの他の研究分野とのかかわりの中で研究が進められている、ということでしょう。これらの分野はそれぞれ研究対象も手法も大きく異なりますが、ある分野が進展することで複素力学系に関する研究が大きく進展したり、逆に複素力学系の研究成果を用いて他分野の研究がなされたりしています。本稿では複素力学系という分野の大まかな紹介の後に、例として筆者の専門である非アルキメデス的力学系について、その概説と複素力学系との関係を紹介します。
マンデルブロ集合とジュリア集合
前述した漸化式 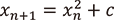 を考えます。もっとも単純なケースは
を考えます。もっとも単純なケースは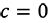 の場合、つまり
の場合、つまり 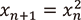 という漸化式が定める力学系でしょう。この漸化式は一般項
という漸化式が定める力学系でしょう。この漸化式は一般項 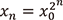 を持つので、漸近挙動は初期値
を持つので、漸近挙動は初期値 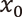 の絶対値によって次のように場合分けできます。
の絶対値によって次のように場合分けできます。
(a) 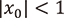 の場合:
の場合: 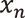 は
は  に収束する;
に収束する;
(b) 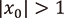 の場合:
の場合: 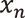 は発散する;
は発散する;
(c) 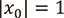 の場合:任意の
の場合:任意の 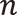 に対して
に対して 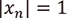 。
。
このとき、(a)や(c)の場合は初期値の微小な変動に対して漸近挙動が安定していることが分かります。つまり、 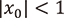 (あるいは
(あるいは 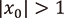 )を変えない範囲で
)を変えない範囲で 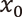 の値を動かしたとしても、最終的に
の値を動かしたとしても、最終的に  に収束(あるいは発散)します。一方で(b)では初期値の微小変動で漸近挙動が大きく変わってしまいます。このように漸近挙動が不安定になる点の集合はジュリア集合と呼ばれています。この場合は複素平面上で
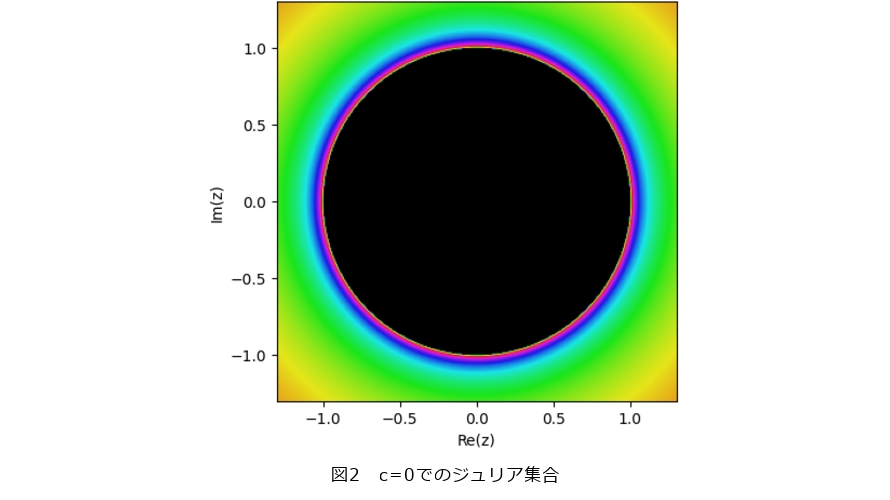
に収束(あるいは発散)します。一方で(b)では初期値の微小変動で漸近挙動が大きく変わってしまいます。このように漸近挙動が不安定になる点の集合はジュリア集合と呼ばれています。この場合は複素平面上で 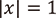 を満たす点の集合、つまり図2にあるような単位円周です。しかし、すべてのジュリア集合が単位円周のように単純な形をしているわけではありません。例えば、
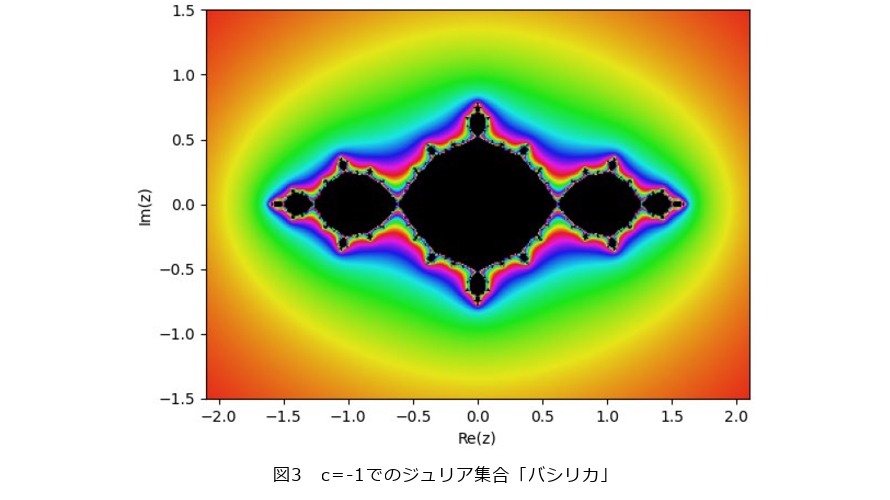
を満たす点の集合、つまり図2にあるような単位円周です。しかし、すべてのジュリア集合が単位円周のように単純な形をしているわけではありません。例えば、 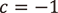 、 つまり漸化式
、 つまり漸化式 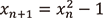 に対応するジュリア集合を描画すると図3のようになります。このジュリア集合は、その形状から「バシリカ*1」と呼ばれています。また、
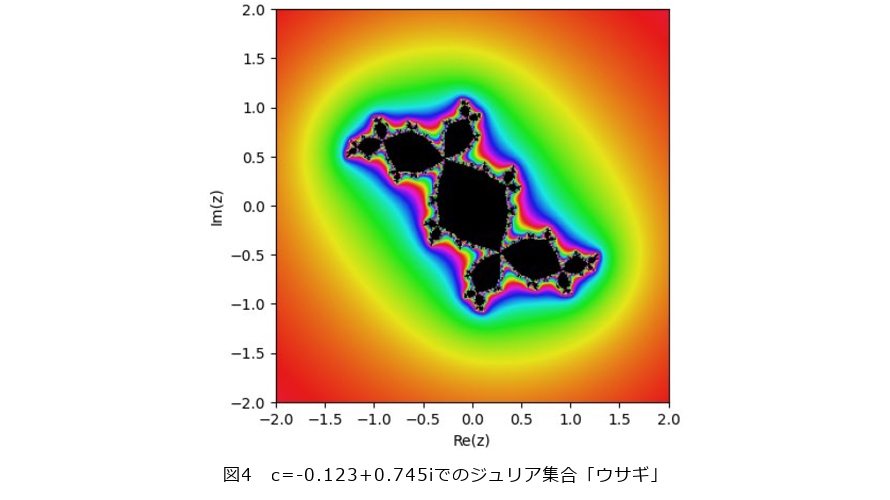
に対応するジュリア集合を描画すると図3のようになります。このジュリア集合は、その形状から「バシリカ*1」と呼ばれています。また、  とすれば図4の「ウサギ」を、
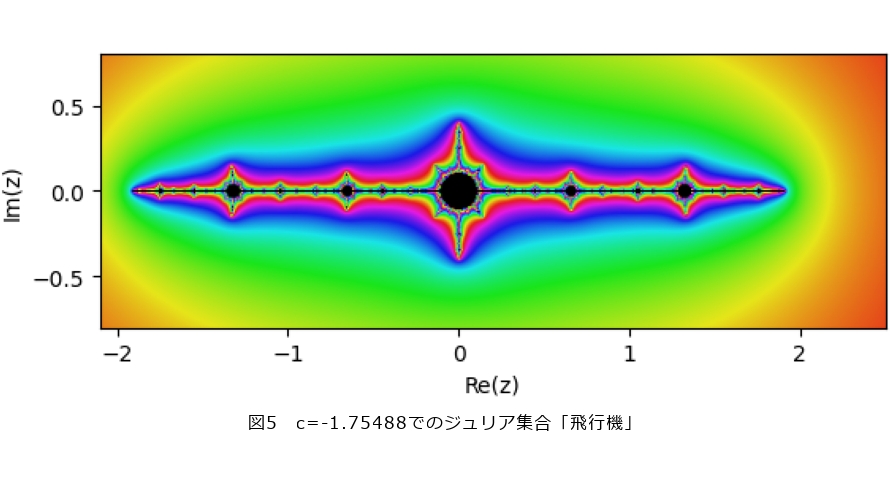
とすれば図4の「ウサギ」を、 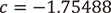 とすれば図5の「飛行機」を得ます。パラメータ
とすれば図5の「飛行機」を得ます。パラメータ![]() を変えるだけで多様な形のジュリア集合を得ることができるのが見てとれます。
を変えるだけで多様な形のジュリア集合を得ることができるのが見てとれます。
冒頭のマンデルブロ集合はこのジュリア集合の「形」を統制しているものです。マンデルブロ集合は漸化式 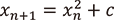 における、パラメータ空間(変数
における、パラメータ空間(変数  の空間)の部分集合で、その内側をいくつもの部屋に分ける複雑な形をしています。複素平面から点
の空間)の部分集合で、その内側をいくつもの部屋に分ける複雑な形をしています。複素平面から点  を選ぶごとに漸化式
を選ぶごとに漸化式 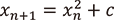 が、さらにそこからそのジュリア集合が対応するため、パラメータ
が、さらにそこからそのジュリア集合が対応するため、パラメータ  を連続的に動かせばそれに応じてジュリア集合が変形していくことが予想されます。実際、同じ部屋の中でパラメータを動かす限りではジュリア集合は連続的に変形します。つまり、現れるジュリア集合の形もよく似たものになります。しかし、マンデルブロ集合をまたぐとそれが全く異なる形に変わってしまうのです。例えば
を連続的に動かせばそれに応じてジュリア集合が変形していくことが予想されます。実際、同じ部屋の中でパラメータを動かす限りではジュリア集合は連続的に変形します。つまり、現れるジュリア集合の形もよく似たものになります。しかし、マンデルブロ集合をまたぐとそれが全く異なる形に変わってしまうのです。例えば 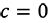 は中心にあるカージオイド状の領域(もっとも大きい領域)の内部、
は中心にあるカージオイド状の領域(もっとも大きい領域)の内部、 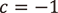 (バシリカ)はその左側の円状の領域の内部、また
(バシリカ)はその左側の円状の領域の内部、また  (ウサギ)はカージオイドの上部に接している円状領域内の点であり、それぞれマンデルブロ集合によって分割された異なる領域に存在しています。各領域の内部ではそれぞれの形を保ったままで変形しますが、一度領域をまたぐとそれがただの円状の集合に変わってしまったり、全く別の形のジュリア集合が現れたりします。このような現象(パラメータの微小変形でジュリア集合の形が大きく変わること)を分岐と呼び、分岐が起きるパラメータを分岐点と呼びます。マンデルブロ集合とは漸化式
(ウサギ)はカージオイドの上部に接している円状領域内の点であり、それぞれマンデルブロ集合によって分割された異なる領域に存在しています。各領域の内部ではそれぞれの形を保ったままで変形しますが、一度領域をまたぐとそれがただの円状の集合に変わってしまったり、全く別の形のジュリア集合が現れたりします。このような現象(パラメータの微小変形でジュリア集合の形が大きく変わること)を分岐と呼び、分岐が起きるパラメータを分岐点と呼びます。マンデルブロ集合とは漸化式 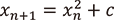 のパラメータ
のパラメータ  に関する分岐点全体の集合のことです。ジュリア集合がパラメータを固定した際の初期値に関する安定性の概念だったのに対し、マンデルブロ集合(より一般に分岐点の集合)は力学系そのものをパラメータで変動した際の系の安定性にかかわる概念である、と理解することができます。
に関する分岐点全体の集合のことです。ジュリア集合がパラメータを固定した際の初期値に関する安定性の概念だったのに対し、マンデルブロ集合(より一般に分岐点の集合)は力学系そのものをパラメータで変動した際の系の安定性にかかわる概念である、と理解することができます。
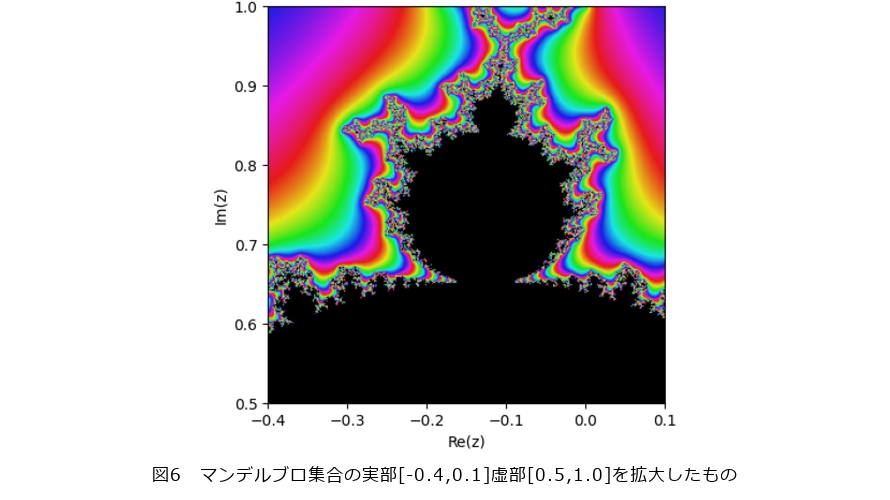
ジュリア集合やマンデルブロ集合は非常に豊かな性質を有しています。例えばバシリカや飛行機などのジュリア集合は複雑ながらどこか規則的な形状をしています*2。実はマンデルブロ集合も同様の性質を持ち、図6のように図を拡大することで何らかの規則が見てとれます。また、あるパラメータの周辺を拡大するとそのパラメータに対応するジュリア集合と同じ形が現れることも知られています。ジュリア集合やマンデルブロ集合の幾何学的性質は興味深い一方で非常に難しく、例えばマンデルブロ集合の局所連結性と呼ばれる性質は今なお未解決の問題です。
漸化式やパラメータの取り方を変えても同様にジュリア集合や分岐点を考えることができます。3次以上の多項式を考える場合パラメータ空間は高次元になり得ますし、漸化式そのものを高次元にすることもできます。例えばエノン写像と呼ばれる写像の定める力学系は、 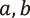 をパラメータとして
をパラメータとして 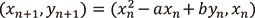 という形をした2変数の力学系です。元々は気候をモデル化したローレンツ方程式と呼ばれる微分方程式が生み出す力学系のカオス現象を解析するためにエノンによって考察された実数の空間での力学系ですが、現在は複素力学系分野でも盛んに研究されています。
という形をした2変数の力学系です。元々は気候をモデル化したローレンツ方程式と呼ばれる微分方程式が生み出す力学系のカオス現象を解析するためにエノンによって考察された実数の空間での力学系ですが、現在は複素力学系分野でも盛んに研究されています。
*1 バシリカ(basilica):建築様式の名称です。
*2 このような性質を持つ図形はフラクタルと呼ばれています。
非アルキメデス的数とその上の力学系
複素力学系が複素数の空間における力学系理論であったのと同じように、非アルキメデス的力学系とは「非アルキメデス的数」の空間における力学系理論です。ただし非アルキメデス的数とはさまざまな種類の数を総合した呼び方で、非アルキメデス的数と呼ばれる数があるわけではありません。もっとも典型的な非アルキメデス的数は 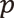 -進数でしょう。
-進数でしょう。 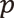 -進数の名前に現れる
-進数の名前に現れる![]() は素数です。「実数」や「複素数」と並列になるのは「2-進数」「3-進数」「5-進数」などの数で、これらは皆似た性質(非アルキメデス性)を持っており、まとめて非アルキメデス数と呼ばれているのです。実際には
は素数です。「実数」や「複素数」と並列になるのは「2-進数」「3-進数」「5-進数」などの数で、これらは皆似た性質(非アルキメデス性)を持っており、まとめて非アルキメデス数と呼ばれているのです。実際には 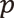 -進数だけではなく後で紹介するローラン級数などもその一種です。ここではまず2-進数を例に非アルキメデス的数の性質をみていきましょう。
-進数だけではなく後で紹介するローラン級数などもその一種です。ここではまず2-進数を例に非アルキメデス的数の性質をみていきましょう。
少々突飛な話ですが、正の整数に普通の距離とは違う2-進距離と呼ばれる距離を考えてみます。この距離は、「2つの数の差が2で割り切れる回数が多ければ多いほど近い」というルールで与えられます。例えば、2と4と8という3つの数を考えてみると、普通の距離の感覚では2と4がもっとも近く、次に4と8が、そして2と8はもっとも遠い、ということになるはずです。しかし、上のルールに従って考えると、4−2=2=21、8−4=4=22、8−2=6=21×3と表せるので、差が2で割り切れる回数は4と8がもっとも多い2回、そして2と4、2と8が共に1回です。つまり、2-進距離では4と8がもっとも近く、2と4、2と8の間の距離は同じ、ということになります。
この距離は実は自然数の2-進展開(バイナリ表示)と大きく関係しています。上に挙げた3種類の数を2-進展開してみると、2=(10)2、4=(100)2、8=(1000)2となります。この2-進展開を右から見ると2と4、2と8は共に最初の1桁のみが一致している一方、4と8は最初の2桁が一致しています。実は、2-進距離は「2-進展開を右から見た際に一致している桁数が多ければ多いほど近い」という距離*3です。これは2-進展開の意味と2-進距離の定義とを比べることで分かります。今後は 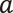 と
と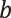 の間の2-進距離を
の間の2-進距離を 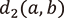 と書き表すことにします。
と書き表すことにします。
ここで、左に無限に続く2-進展開(…111)2を考えてみましょう。この数は、(1)2、(11)2、(111)2、…の極限です。十進法で書き表すと1、3、7、…であり発散するようにみえるこの数列は、実は2-進距離では−1に収束します。実際、この数列に1を足すと(10)2、(100)2、(1000)2、…という数列を得ますが、この数列の極限は (…000)2、つまり0です。(…111)2に1を足すと0になるわけですから、(…111)2 は−1と一致する、ということになります。
一方で、実数のときと同様に小数を考えてみると、2-進展開では小数点以下は2−1 の位、2−2の位、2−3の位と続きますが、2-進距離を拡張するためこれらをそれぞれ2で−1回、−2回、−3回割り切れるとみなします。このとき2-進絶対値(0との間の2-進距離)は桁が右に増えれば増えるほど大きくなるので、右側に無限に続く2-進展開の列は2-進距離では発散します。左側には有限、右側には無限に続く数を考える実数とは真逆の現象が起きていることが観察できます。
2-進数とは、左側には無限に、右側には有限に続く2-進展開で書ける数のことです。上で定義した 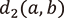 を敷衍し距離や収束の概念が定義できます。実は2-進数の集合は上で考えた負の数だけでなく有理数すべてを含み、実数とは似て異なる性質を持っています。特に重要なのは任意の2-進数
を敷衍し距離や収束の概念が定義できます。実は2-進数の集合は上で考えた負の数だけでなく有理数すべてを含み、実数とは似て異なる性質を持っています。特に重要なのは任意の2-進数 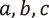 に対して
に対して 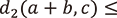
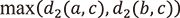 という不等式(強三角不等式)が成りつことです。
という不等式(強三角不等式)が成りつことです。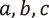 に正の実数を当てはめてみると分かるように、この不等式は実数の距離では成立せず(代わりに弱い形の三角不等式
に正の実数を当てはめてみると分かるように、この不等式は実数の距離では成立せず(代わりに弱い形の三角不等式 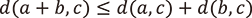 が成り立つ)、これが実数や複素数との間に大きな違いを生み出しています。いくつかの例をもってこの違いをみてみましょう。
が成り立つ)、これが実数や複素数との間に大きな違いを生み出しています。いくつかの例をもってこの違いをみてみましょう。
まず、実数と2-進数の「形」の違いをみます。実数は数直線の上に並んだ数だとみなすことができますが、2-進数はどんな形だと考えるのが妥当でしょうか?そのヒントは2-進展開にあります。簡単のため小数を持たない2-進展開だけを考え、2-進展開を木で表すことを考えます。この木は1つの頂点から始まり、1の位の数が0か1かによって二分され、その先の頂点でまた2の位の数による二分があり、さらに4の位の数に応じて……と、2-進展開の桁に対応するだけの頂点と、そこから下方向に伸びる枝とによって図7のようにルート無限木をつくることができます。小数を持たない2-進数はすべて、この無限木の極限と対応しています。小数を持つ場合は1/2の位、1/4の位に応じて1の位に対応する頂点の上に新しい頂点を付け加えていくことで表現できます。2-進数の「形」はこの無限木、あるいはその極限であるとみなせます。実際、二分木が2-進展開を表し、2-進距離が「2-進展開が一致しているほど近い」という距離であったことを考慮すると、二分木で共有する枝の深さが2-進距離と対応していることが観察できます。
次に2-進数の空間での力学系をみてみましょう。2-進数の空間の上の力学系は前述のものとは大きく異なります。漸化式 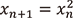 では、漸化式が一般項
では、漸化式が一般項 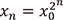 を持ち、漸近挙動を(a)-(c)の三通りに場合分けできるところまでは同じですが、「(b)の場合に漸近挙動が不安定になる」は2-進数の場合正しくありません。これを詳しくみるため、絶対値が1である(
を持ち、漸近挙動を(a)-(c)の三通りに場合分けできるところまでは同じですが、「(b)の場合に漸近挙動が不安定になる」は2-進数の場合正しくありません。これを詳しくみるため、絶対値が1である(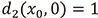 を満たす)数
を満たす)数 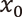 を考えてみます。この
を考えてみます。この 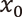 を絶対値が1よりも小さな数
を絶対値が1よりも小さな数 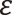 で変動させると、得られる数
で変動させると、得られる数 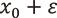 の絶対値は強三角不等式より
の絶対値は強三角不等式より 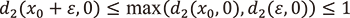 を満たします。つまり(c)の状態にはなり得ません。実は
を満たします。つまり(c)の状態にはなり得ません。実は![]() の絶対値が1よりも真に小さいとき、
の絶対値が1よりも真に小さいとき、 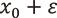 の絶対値はちょうど1になる、つまり(a)の状態にもならないことが強三角不等式のみから証明できます。つまり、2-進距離での微小変形は(b)の条件を崩さないのです。実は2-進数の空間の上での漸化式
の絶対値はちょうど1になる、つまり(a)の状態にもならないことが強三角不等式のみから証明できます。つまり、2-進距離での微小変形は(b)の条件を崩さないのです。実は2-進数の空間の上での漸化式 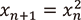 はジュリア集合を持ちません。非アルキメデス性が力学系の振る舞いに大きな影響を与えていることが見てとれると思います。
はジュリア集合を持ちません。非アルキメデス性が力学系の振る舞いに大きな影響を与えていることが見てとれると思います。
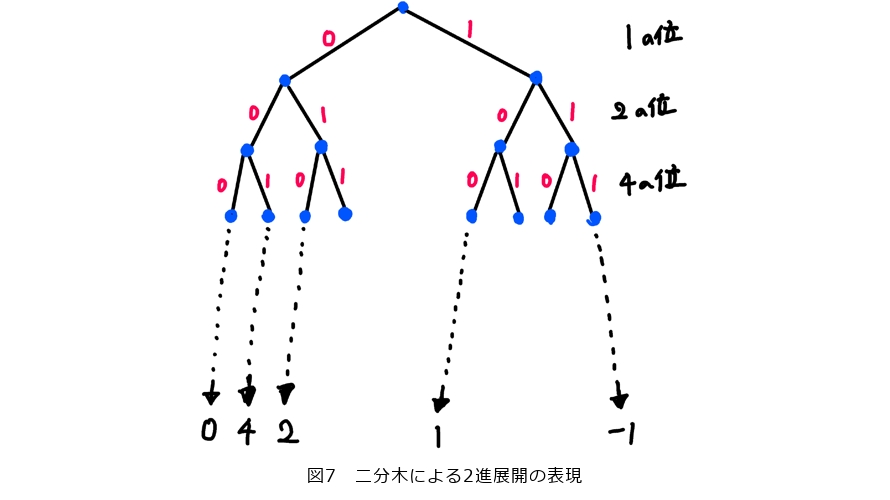
少し話を戻しますが、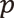 -進数とは上の議論での2-進展開を3-進展開、5-進展開など他の素数に置き換えて得られる数のことです。すべて上述の強三角不等式を満たし似た性質を持つものの、素数を変えるごとに得られる距離はすべて異なり、
-進数とは上の議論での2-進展開を3-進展開、5-進展開など他の素数に置き換えて得られる数のことです。すべて上述の強三角不等式を満たし似た性質を持つものの、素数を変えるごとに得られる距離はすべて異なり、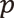 -進数は素数の数だけ存在します。そして上で触れたとおり、強三角不等式によって力学系もまた実数や複素数の上の力学系とは異なる様相を呈します。これらは一見奇妙で非直感的に思えるかもしれませんが、整数論においてはもっとも基本的かつ重要なツールの1つといっても過言ではなく、例えばフェルマーの最終定理の証明でも用いられています。
-進数は素数の数だけ存在します。そして上で触れたとおり、強三角不等式によって力学系もまた実数や複素数の上の力学系とは異なる様相を呈します。これらは一見奇妙で非直感的に思えるかもしれませんが、整数論においてはもっとも基本的かつ重要なツールの1つといっても過言ではなく、例えばフェルマーの最終定理の証明でも用いられています。
*3 具体的にははじめのn桁が一致しているときに距離を2‒nである、と定めることが多いです。
非アルキメデス的力学系とハイブリッド力学系
最後に複素力学系における非アルキメデス的力学系の応用について紹介します。ここでは例として、 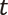 でパラメータ付けされた 漸化式
でパラメータ付けされた 漸化式  を考えます。この漸化式は前述のものとは異なり、
を考えます。この漸化式は前述のものとは異なり、 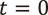 のとき
のとき 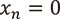 となってしまいます。しかし
となってしまいます。しかし 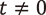 を保つ範囲ではこの漸化式は非自明な力学系を定めており、
を保つ範囲ではこの漸化式は非自明な力学系を定めており、  の周りで何か大きな変化が起きていることが見てとれます。このような現象を数学では退化と呼んでいます。同じ形の漸化式でありながら力学系の漸近挙動が変わってしまう分岐に対し、漸化式の形そのものが大きく変わってしまうのが退化です。退化現象はパラメータ空間のコンパクト化と呼ばれる理論と関係している力学系の重要な問題の1つで、この退化現象を非アルキメデス的力学系によって理解するために用いられるのがハイブリッド空間上の力学系(ハイブリッド力学系)理論です。ハイブリッド空間はブックサム、ファーブル、ジョンソンの3名の数学者によって考案され、元々は代数幾何学の研究のために生み出されました(1)が、その後ファーブルによって力学系の退化の研究へと輸入されました。この研究で用いられる非アルキメデス数は上で考えていた
の周りで何か大きな変化が起きていることが見てとれます。このような現象を数学では退化と呼んでいます。同じ形の漸化式でありながら力学系の漸近挙動が変わってしまう分岐に対し、漸化式の形そのものが大きく変わってしまうのが退化です。退化現象はパラメータ空間のコンパクト化と呼ばれる理論と関係している力学系の重要な問題の1つで、この退化現象を非アルキメデス的力学系によって理解するために用いられるのがハイブリッド空間上の力学系(ハイブリッド力学系)理論です。ハイブリッド空間はブックサム、ファーブル、ジョンソンの3名の数学者によって考案され、元々は代数幾何学の研究のために生み出されました(1)が、その後ファーブルによって力学系の退化の研究へと輸入されました。この研究で用いられる非アルキメデス数は上で考えていた 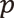 -進数ではなく、(一次元の)複素ローラン級数と呼ばれる数です。複素ローラン級数とは、
-進数ではなく、(一次元の)複素ローラン級数と呼ばれる数です。複素ローラン級数とは、 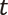 を変数とする有限個の負冪を許した複素係数の級数
を変数とする有限個の負冪を許した複素係数の級数 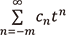 のことです。収束半径などの条件はないため、
のことです。収束半径などの条件はないため、 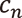 の値によっては原点の周りの有理型関数を定義しない形式的な級数ですが、原点の周辺で定義される有理型関数を自然に含んでいます。「左側(負冪)には有限に、右側には無限に続く数の列」という意味で2-進展開と似ていることが観察できます。実際、2つの級数
の値によっては原点の周りの有理型関数を定義しない形式的な級数ですが、原点の周辺で定義される有理型関数を自然に含んでいます。「左側(負冪)には有限に、右側には無限に続く数の列」という意味で2-進展開と似ていることが観察できます。実際、2つの級数 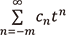 と
と 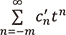 について、
について、  が任意の
が任意の 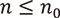 まで成立する(「
まで成立する(「 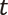 -進展開が
-進展開が 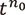 の位まで一致する」)ときにこの2つの級数の距離を
の位まで一致する」)ときにこの2つの級数の距離を 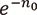 である、と定めることで複素ローラン級数は非アルキメデス的数になります。このとき、
である、と定めることで複素ローラン級数は非アルキメデス的数になります。このとき、 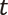 を複素ローラン級数であるとみなすことで、漸化式
を複素ローラン級数であるとみなすことで、漸化式 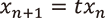 を複素ローラン級数の空間の力学系だとみなすことができます。ハイブリッド力学系とは、大まかにいえばこの複素ローラン級数の力学系と元々の複素力学系の間の関係を記述するものです。
を複素ローラン級数の空間の力学系だとみなすことができます。ハイブリッド力学系とは、大まかにいえばこの複素ローラン級数の力学系と元々の複素力学系の間の関係を記述するものです。
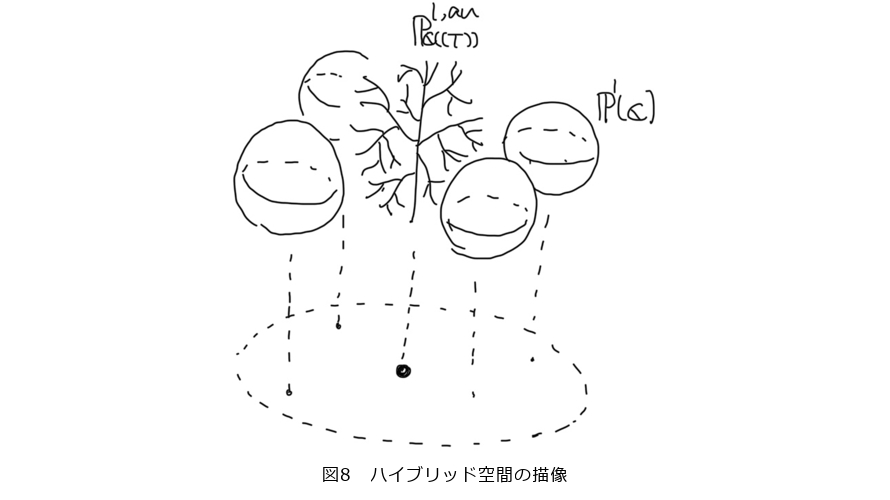
ハイブリッド空間は図8のような形をしています。複素数 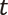 でパラメータ付けされた空間で、
でパラメータ付けされた空間で、 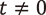 を満たす限り複素数の空間を与えるのですが、
を満たす限り複素数の空間を与えるのですが、  では複素ローラン級数の空間を与えます。つまり、複素数の空間が複素ローラン級数の空間に「退化」しているのです。ここで複素ローラン級数の空間として考えているのは実際にはベルコヴィッチ空間と呼ばれるもので、内実は非常に難解であるため割愛しますが、大雑把には前述した木の全体を考えたような空間です。極限には非アルキメデス的数(ここでは複素ローラン級数)が現れるので、漸化式に級数を代入するごとに極限の点たちが漸化式に従って動き、それに合わせるかたちで内部の木も動く、というイメージを持っていれば十分です。この木構造を持つ複素ローラン級数の空間が、複素数の空間の退化の「極限」だとみなせる、というのがハイブリッド空間の大まかな描像です。
では複素ローラン級数の空間を与えます。つまり、複素数の空間が複素ローラン級数の空間に「退化」しているのです。ここで複素ローラン級数の空間として考えているのは実際にはベルコヴィッチ空間と呼ばれるもので、内実は非常に難解であるため割愛しますが、大雑把には前述した木の全体を考えたような空間です。極限には非アルキメデス的数(ここでは複素ローラン級数)が現れるので、漸化式に級数を代入するごとに極限の点たちが漸化式に従って動き、それに合わせるかたちで内部の木も動く、というイメージを持っていれば十分です。この木構造を持つ複素ローラン級数の空間が、複素数の空間の退化の「極限」だとみなせる、というのがハイブリッド空間の大まかな描像です。
このような空間を考えることにはさまざまな理由がありますが、1つには数学者の自然なものの見方が関係しています。漸化式 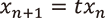 は
は  で退化し、ただの定数になってしまいますが、これは「誤った」空間で漸化式を見ているせいでそのようなおかしな現象が起きているのだ、と考えるのです。つまりおかしな現象が起きないような「正しい」空間の上で漸化式を見ればよいのです。ハイブリッド空間はその答えの1つで、この場合「正しい」極限は上で考えた複素ローラン級数の上の力学系である、ということになります。
で退化し、ただの定数になってしまいますが、これは「誤った」空間で漸化式を見ているせいでそのようなおかしな現象が起きているのだ、と考えるのです。つまりおかしな現象が起きないような「正しい」空間の上で漸化式を見ればよいのです。ハイブリッド空間はその答えの1つで、この場合「正しい」極限は上で考えた複素ローラン級数の上の力学系である、ということになります。
ファーブルは 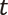 でパラメータ付けされていて
でパラメータ付けされていて  で退化する1変数の力学系において、
で退化する1変数の力学系において、 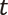 を固定するごとに定まるジュリア集合が
を固定するごとに定まるジュリア集合が 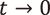 で複素ローラン級数上の力学系のジュリア集合にある意味で収束することを証明しました(2)*4。また、筆者の論文(3)では同様の事実がエノン写像の力学系でも成立することを証明しており、また、他のさまざまな複素力学系の退化でも同様の現象が起きることが期待されます。複素数とは大きく異なっているようにみえる非アルキメデス的数ですが、実は複素力学系の退化を統一的なかたちで記述する重要な対象なのです。
で複素ローラン級数上の力学系のジュリア集合にある意味で収束することを証明しました(2)*4。また、筆者の論文(3)では同様の事実がエノン写像の力学系でも成立することを証明しており、また、他のさまざまな複素力学系の退化でも同様の現象が起きることが期待されます。複素数とは大きく異なっているようにみえる非アルキメデス的数ですが、実は複素力学系の退化を統一的なかたちで記述する重要な対象なのです。
*4 ファーブルが参考文献(2)で実際に証明したのはn次元の射影空間と呼ばれる空間の上の力学系における結果ですが、詳細は割愛します。
おわりに
数学の分野の名前は研究技法を示している場合と研究対象を示している場合とがありますが、「複素力学系」は研究対象を示す名称です。複素数の空間の上に定められた力学系を対象として、それぞれの研究者が好きな道具を用いてさまざまな角度から研究を進めています。本稿ではその一例として非アルキメデス的力学系を用いた研究の方向性を紹介しましたが、ほかにもさまざまなアプローチによって多くの興味深い定理が日夜証明されています。本稿を通じてその面白さが少しでも伝われば幸いです。
■参考文献
(1) S. Boucksom and M. Jonsson:“Tropical and non-Archimedean limits of degenerating families of volume forms,”JEP, Vol. 4, pp. 87-139, 2017.
(2) C. Favre:“DEGENERATION OF ENDOMORPHISMS OF THE COMPLEX PROJECTIVE SPACE IN THE HYBRID SPACE,”JIMJ, Vol. 19, No. 4, pp. 1141-1183, 2020.
(3) https://arxiv.org/abs/2212.10851

色川 怜未







NTT基礎数学研究センタでの研究に興味を持ってくださり大変光栄に思います。なるべく純粋数学を学んだことのない方にも魅力がお伝えできるよう努力しましたので、楽しく読んでいただけたら幸いです。