「コヒーレントイジングマシンの研究」と「多光子量子もつれを用いた通信」の2テーマを軸に研究を進めています。
イジングマシンとは、イジングモデルを模擬する物理シミュレータ、ということができます。イジングモデルとは、相互作用するスピン群の振る舞いを記述する理論モデルです。スピンとは、粒子が持つ角運動量であり、ここでは2値のいずれかをとる量です。多くの組合せ最適化問題は、イジングモデルにおいてエネルギーが最小となるスピン値の組合せを求める問題に変換できます。よって、イジングマシンを用いた物理実験によりエネルギー最小となるスピン配列を求めることで、解きたい組合せ最適化問題の解を効率良く得ることができます。
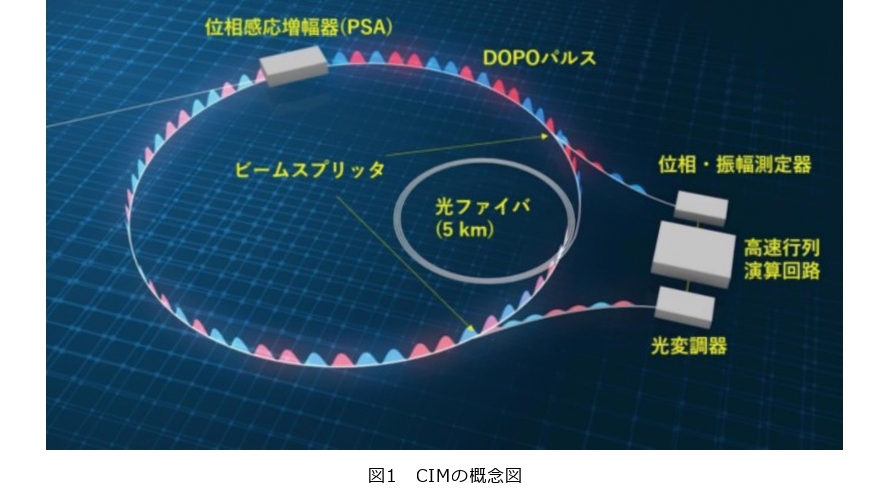
私たちは、内閣府の主導する革新的研究開発推進プログラム（ImPACT）において各研究機関と共同で、このイジングモデルの計算を、光パラメトリック発振器と呼ばれる特殊なレーザ光の位相（0,π）をスピンの代わりとして用いることで計算を安定的かつ高速に行う、2コヒーレントイジングマシン（CIM）を2016年に実現しました（図1）。さらにスピン数を2000から10万にまで拡大したCIMを2021年にScience Advances誌より発表しています。これらの発表は大きな反響を呼び、多くの論文に引用されており、また世界の多くの機関からさまざまな新しいイジングマシンが提案されるに至っています。私自身も多くの国際会議から招待講演の依頼をいただいたり、国際会議や海外論文誌の委員等を依頼されることも増えてきました。今後さらにイジングマシンが発展して、新しい分野として確立されればよいと思っています。自分たちもイジングマシン分野の先駆者として、さらにCIMを進展させられるよう、研究に取り組んでいます。こうした中で、最近2つの成果を出すことができました。
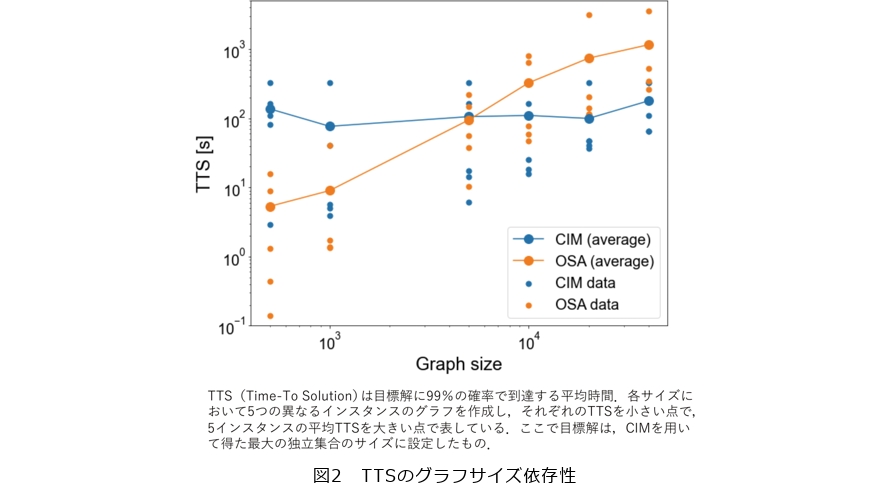
1つは、「磁場項のある問題の解探索」に関するものです。CIMのような物理イジングマシンを研究する機関は多くなってきたのですが、物理イジングマシンの大部分は「磁場項のない問題」しか解いていません。磁場項とは、イジングモデルの数式において、各スピンに対してその向きをプラスもしくはマイナスにしようとする外部からの磁場に相当する項のことで、「磁場項のない」問題とは、スピンどうしの相互作用項のみの基本的な最適化問題です。私たちのチームが最初のCIM実験でこの基本的な問題を解いたこともあり、他の多くの研究機関の物理イジングマシンも、磁場項のない問題を用いた評価を行ってきました。しかし、実際の最適化問題のほとんどは「磁場項のある問題」なので、この問題を用いた性能評価がCIMの実応用に向けては重要です。私たちは、CIMにおいていくつかのスピンを補助スピンとして用いることで磁場項を実装する手法を提案し、それを用いて磁場項のある代表的な問題の1つである「最大独立集合問題」の解探索をCIMおよび従来のデジタル計算機上で実装した最適化焼きなまし法(OSA：Optimized Simulated Annealing)を用いて行いました。ノード数が500から40000までのグラフを生成し、目標解に到達する平均時間を比較しました（図2）。その結果、問題サイズが小さいときはOSAのほうが速く目標解を得ますが、ノード数5000くらいで同程度の性能となりました。さらにそれより大きな問題サイズではCIMがOSAより早く目標解を得ることができ、その差は問題サイズが大きくなるほど拡大する傾向にあることが示されました。この論文は、2025年2月にハイインパクトジャーナルである『Science Advances（Science誌の姉妹誌）』に掲載されました^（1）。今回「磁場項がある問題」を物理イジングマシンであるCIMで解いたことで、イジングマシン分野の研究全体を一歩進めたと考えています。
そして、もう1つは「CIMの本質に迫る」というテーマです。私たちが、「測定・フィードバック」により光パラメトリック発振器を結合するCIMを2016年に発表した直後から、測定・フィードバックは統計物理学でよく知られている近似手法である「平均場近似」と同じではないか、という疑問が指摘されていました。
平均場近似は、統計物理学においてよく知られている手法で、多数の粒子間の相互作用を考慮する多体問題を、一体問題に帰着させる近似手法です。平均場近似では、多数の粒子それぞれが他のすべての粒子から受ける相互作用を平均的な効果としてとらえ、個々の粒子の相互作用は無視し、代わりに平均的な「場」の中で粒子1つひとつが振舞うと仮定します。平均場近似は多体問題の計算を簡略化できる一方、一般に計算精度は低下します。
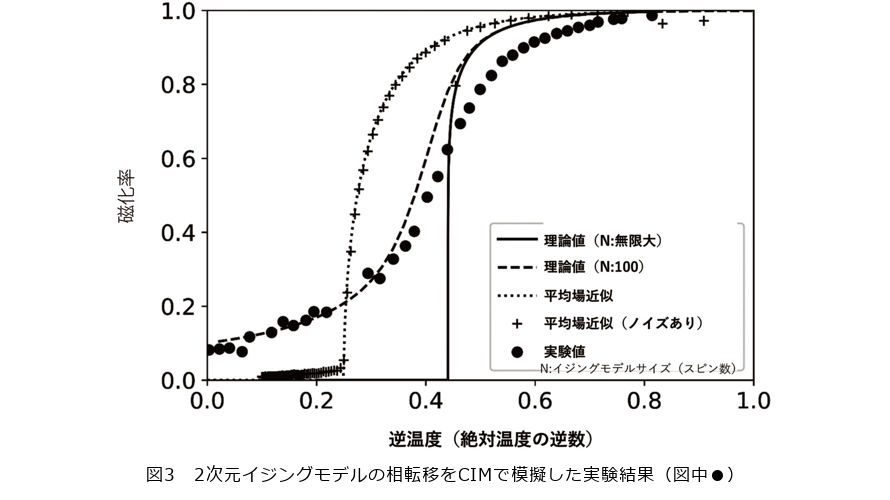
「CIMは平均場近似ソルバではないか」という疑問を明らかにするための方法を思案する中で、「2次元イジングモデルの相転移」をCIMで再現すればいい、ということに気付きました。2次元の平方格子イジングモデルは、ノーベル賞受賞者であるOnsagerにより厳密解が導出された重要な理論モデルで、明瞭な相転移を示すことが知られています。一方、2次元イジングモデルの平均場近似解もよく知られており、その相転移温度は厳密解のそれと明瞭に違います。「2次元イジングモデルの相転移」をCIMで再現実験した結果は、図3に示すように、理論と完全に一致はしないものの、CIMは明らかに「平均場近似」ではなく「厳密解」に近い振る舞いをすることが確認できました。これは、「CIMは平均場近似ソルバではなく、多体系を模擬する物理シミュレータである」ということを強く示唆するものと考えています。この結果は、2023年3月に学会誌『Physical Review Applied』より出版され^（2）、私たちに投げかけられていた問いに答えられたのではと考えています。

私は2003年から「量子もつれ」に関する研究をしてきました。量子もつれとは、2つ以上の粒子間に古典的には説明できない相関が存在している量子状態です。量子もつれは、1935年のアインシュタインらの論文（EPR論文）においてその存在が論じられるようになり、その後量子の相関についてさまざまな研究がなされてきました。2022年に、フランスのパリ・サクレー大学アラン・アスペ博士、米国のクラウザー研究所ジョン・クラウザー博士、オーストリアのウィーン大学アントン・ツァイリンガー博士による量子もつれの実験研究に対してノーベル賞が授与されています。
私は、2004年に、当時の上司であった井上恭先生（現大阪大学名誉教授）の指導のもと、光ファイバ中で1.5μmの波長帯における光子の量子もつれを生成しました^（3）。これは、Northwestern大学のPrem Kumarグループと並び世界で初めて光ファイバで量子もつれを発生した実験であり、私としての量子もつれ研究の原点となるものです。この実験は2つの光子による量子もつれでしたが、上に述べたツァイリンガー先生のグループなどでは多光子による量子もつれの研究が進められ3個以上の量子もつれ光子状態も生成できるようになりました。これらのグループのほとんどでは、光子の偏波状態に関する量子もつれ状態を生成していました。
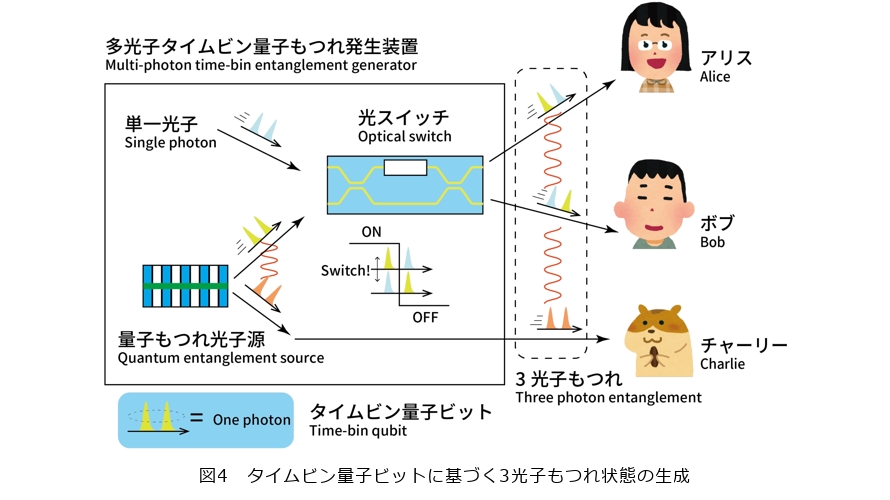
偏波を利用した量子ビットは、自由空間では制御が容易である反面、光ファイバ中の伝送においては光ファイバの屈折率の揺らぎや偏波モード分散により擾乱を受ける問題があります。私たちは、光ファイバを用いた量子通信への応用を考えて、光子の時間位置に関する重ね合わせ状態を使った安定した量子ビットである「タイムビン量子ビット」に基づく3光子もつれ状態の研究を進め、世界で初めてこれを実現しました（2023年2月）^（4）。「多光子タイムビン量子もつれ発生装置」では、量子もつれ光子源からの2光子量子もつれのうちの片方の光子と単一の光子を光スイッチに入力することでこれらの光子を「もつれさせる」ことで、量子もつれ光子源からの残された量子もつれ状態の光子との3光子の間で量子もつれ状態を生成します（図4）。こうして生成された3光子は、それぞれの光子の測定結果は完全にランダムになりますが、3光子の測定結果間には明瞭な相関があるという性質を持ちます。これを利用して、例えば量子力学の原理に基づき絶対に安全な暗号通信である「量子暗号」を3者間で実現することが可能となります。
2023年度から、総務省の国家プロジェクトである「量子インターネット実現に向けた要素技術の研究開発」に参加し、国立研究開発法人情報通信研究機構（NICT）をはじめ、大阪大学、横浜国立大学、学習院大学、東北大学とともに研究を進めています。プロジェクトの期間は2027年度までですが、プロジェクトの成果の一つとして、私たちのこのタイムビン多光子もつれを使った量子通信のプロトタイプをお見せできるようにしたいと思っています。

個人的な話なのですが、2024年の1月に、私の友人でかつての共同研究者であった米国立標準技術研究所(NIST：National Institute of Standards and Technology)のSae Woo Nam博士がご病気のためお亡くなりになりました。Sae Wooは私が米国のスタンフォード大学で山本喜久教授の研究室で客員研究員であったとき、縁があり一緒に量子暗号の実験を行った仲間です。彼は私と同世代（Sae Wooが1つ年上）で、夜中に実験室で研究の進め方をめぐって激論（口論？）したりもしましたが、一緒に素晴らしい実験結果を出してハイインパクトジャーナルである『Nature Photonics』から出版することができ、さらに数年後には私がNISTの客員研究員となって米国Boulderに滞在し、共に世界最長距離の光ファイバ上の量子テレポーテーション実験を行ったりもしました。その後の彼は、超伝導光子検出器の研究を分野として確立し、量子情報実験における私たちの世代の世界トップ研究者の1人となりました。彼からは超伝導光子検出器について多くの知識、ノウハウを教わりましたが、私自身彼の研究スタイルにも大きく影響されました。
何より第一に、Sae Wooは「Hard worker」でした。彼はマサチューセッツ工科大学（MIT)を卒業してスタンフォード大学で博士号を取得した秀才ですが、同時に冷凍機の中の超伝導デバイスの配線のような泥臭い作業を根気強く率先して行う技術者でもありました。また、彼は当時すでにNISTのグループリーダーでしたが、部下にだけやらせるのではなく、自分が率先して実験を行い、その背中で部下を指導するという人でした。
何より、彼は（共同研究でスタンフォード大学に来たように）さまざまなバックグラウンドを持つ共同研究者と積極的に交流し、仲間をつくって研究することで、さらに自分や自分のチームを強くする、というやり方を貫いていました。自分たちだけでなく、私を含め共同研究者も強くしてくれたと思います。彼は自分のつくり上げた超伝導光子検出器を自分の車に詰め込んで米国の多くの大学を訪問し、そこで共同研究をしていました（その後日本にも、超伝導光子検出器を飛行機の手荷物にして来日しました）。まさに、「外に出る」研究者でした。
私自身、こうしたSae Wooのスタイルに大きく影響されています。私は彼と同じようにハードワーカーである反面、ほとんど1人で実験をしていました。彼の仕事ぶりを見て、ときには「外に出て」研究することで、より素晴らしい成果が得られ、これまでより大きな世界に踏み出せる、といったことを意識するようになりました。

私はSae Wooに限らず多くの方の研究姿勢に影響されていますが、研究のやり方は本当に人それぞれで、いろいろな人を参考にしつつも、結局は自分のやり方をつくっていくしかありません。とはいえ、1つだけメッセージを送るとすれば、「たまには外に出よう」といったところでしょうか。「外」とは海外や他のグループ、研究機関であったり、他の分野であったり、これまでの自分の枠の外、という意味です。私自身、2003年にNTTアクセスサービスシステム研究所からNTT物性科学基礎研究所に社内公募で異動し量子の世界に飛び込んだり、2004年にスタンフォード大学の山本グループに共同研究で滞在したり、2015年にCIMのプロジェクトに参加したりと何度か「外に出て」いますが、そのたびに新しい分野に飛び込み、新しい人に会い、新しいことを学びました。もちろん新しい分野で戸惑うことも多いですが、違う分野でこそ私の知識やスキルが役に立つと感じることも多々ありますし、何より研究者として新しい方向性を獲得していったように思います。一言でいうなら、「現場でハードワークし、たまには外に出る」。皆様の参考になれば幸いです。

■参考文献
（1）　H. Takesue, K. Inaba, T. Honjo, Y. Yamada, T. Ikuta, Y. Yonezu, T. Inagaki, T. Umeki, and R. Kasahara： “Finding independent sets in large-scale graphs with a coherent Ising machine,” Sci. Adv., Vol.11, No.7，eads7223, 2025.
（2）　H. Takesue, Y. Yamada, K. Inaba, T. Ikuta, Y. Yonezu, T. Inagaki, T. Honjo, T. Kazama, K. Embutsu, T. Umeki, and R. Kasahara: “Observing a phase transition in a coherent Ising machine,” Phys. Rev., Applied, Vol.19, L031001, 2023.
（3）　H. Takesue and K. Inoue: “Generation of polarization-entangled photon pairs and violation of Bell’s inequality using spontaneous four-wave mixing in a fiber loop,” Phys. Rev. A, Vol.70, 031802, 2004.
（4）　H. P. Lo, T. Ikuta, K. Azuma, T. Honjo, W. J. Munro, and H. Takesue: “Generation of a time-bin Greenberger-Horne-Zeilinger state with an optical switch,” Quantum Sci. Technol., Vol.8, No.3, 035003, 2023.