2024年7月号
特集
数論・代数幾何・表現論が紡ぐ数学の世界
- 楕円曲線
- ガロア理論
- ゼータ関数
NTT基礎数学研究センタでは、数学の基礎研究をとおして科学技術の源泉である「知の泉」をより豊かにしたいと考えています。本稿ではまず、NTT基礎数学研究センタでの研究の全体像を俯瞰します。さらに、センタの中心的な研究領域である「数論、特に数論力学系」「代数幾何・数論幾何」「表現論・保型形式」について紹介します。
佐野 薫(さの かおる)/宮﨑 弘安(みやざき ひろやす)
若山 正人(わかやま まさと)
NTT基礎数学研究センタ
数論・代数幾何・表現論が紡ぐ数学の世界
およそ2500年前のギリシャで、素数の研究がなされたことは驚きです。素数が無限に存在することや自然数が素数の積に一意に分解できることが示されていました。どんな動機があったのかは不明です。しかも1977年のリベスト、シャミア、エーデルマンによるRSA暗号方式の発明まで、その工学や社会での応用は期待さえありませんでした。加えてRSAの鍵となる「 ![]() を素数、
を素数、![]() を整数とすれば
を整数とすれば ![]() が成り立つ」というフェルマーの小定理(1)の発見(証明はライプニッツ)後も、その確立に300年余を要しました。
が成り立つ」というフェルマーの小定理(1)の発見(証明はライプニッツ)後も、その確立に300年余を要しました。
数論(整数論)は、数、特に整数およびそれから派生する数の体系の性質について研究する数学の一分野です(2)。ここで考える数の体系とは、加減乗除がその中で自由にできる分数全体がなす有理数(整数/整数の形で表せる数)体のような代数体をはじめ、有限集合からなる有限体、有理数列の極限として得られる数全体としての実数体や ![]() 進数全体がなすような局所体と呼ばれるものなどです。数論はローマ帝国時代のディオファントス方程式の研究に起源を持つとされています。ディオファントス方程式とは、有理数を係数とする多項式により定まるものです。できればそれを解きたいのですが、一般には困難です。そこで解も再び有理数になるものに関心が向かいます。というのも無理数(有理数ではない実数)は有理数の極限ということから、数として不完全なものと考えられたからでしょう。有理数は無数にあるものの、実数のほとんどは無理数です。ですが、それを十把一絡げにしてしまうのでは、宇宙の中で暗黒物質について考えないのと同じです。科学としても物足りません。例えば、
進数全体がなすような局所体と呼ばれるものなどです。数論はローマ帝国時代のディオファントス方程式の研究に起源を持つとされています。ディオファントス方程式とは、有理数を係数とする多項式により定まるものです。できればそれを解きたいのですが、一般には困難です。そこで解も再び有理数になるものに関心が向かいます。というのも無理数(有理数ではない実数)は有理数の極限ということから、数として不完全なものと考えられたからでしょう。有理数は無数にあるものの、実数のほとんどは無理数です。ですが、それを十把一絡げにしてしまうのでは、宇宙の中で暗黒物質について考えないのと同じです。科学としても物足りません。例えば、![]() は
は ![]() という無理数の解を持ちます。
という無理数の解を持ちます。![]() や
や ![]() などは代数的数といわれ、円周率
などは代数的数といわれ、円周率 ![]() 、ネイピア数
、ネイピア数 ![]() や
や ![]() などの超越数と区別されます。ところで、
などの超越数と区別されます。ところで、![]() や
や ![]() に対しては、それぞれを定義する有理数極限に戻るまでもなく掛け算の計算
に対しては、それぞれを定義する有理数極限に戻るまでもなく掛け算の計算 ![]() ができます。つまり、代数的数の全体はその中で閉じた数の体系を定めます。さらに、
ができます。つまり、代数的数の全体はその中で閉じた数の体系を定めます。さらに、![]() なども導入され、人類は数という概念を広げてきました。今も、人類には代数的数よりも広い良いクラスの数を見つけたいとの問題意識があります。実際、円周率
なども導入され、人類は数という概念を広げてきました。今も、人類には代数的数よりも広い良いクラスの数を見つけたいとの問題意識があります。実際、円周率 ![]() のような「周期」と呼ばれる積分表示を持つ超越数たちの間に、代数的に統制される広い良いクラスを見出せないかという期待があります。コンセビッチ-ザギエ予想といわれるものです。解決は難しそうですが1つの理想の姿です。なお、これらの数に対する意識は、ギリシャの3大作図問題などとも密接にかかわるものでした。
のような「周期」と呼ばれる積分表示を持つ超越数たちの間に、代数的に統制される広い良いクラスを見出せないかという期待があります。コンセビッチ-ザギエ予想といわれるものです。解決は難しそうですが1つの理想の姿です。なお、これらの数に対する意識は、ギリシャの3大作図問題などとも密接にかかわるものでした。
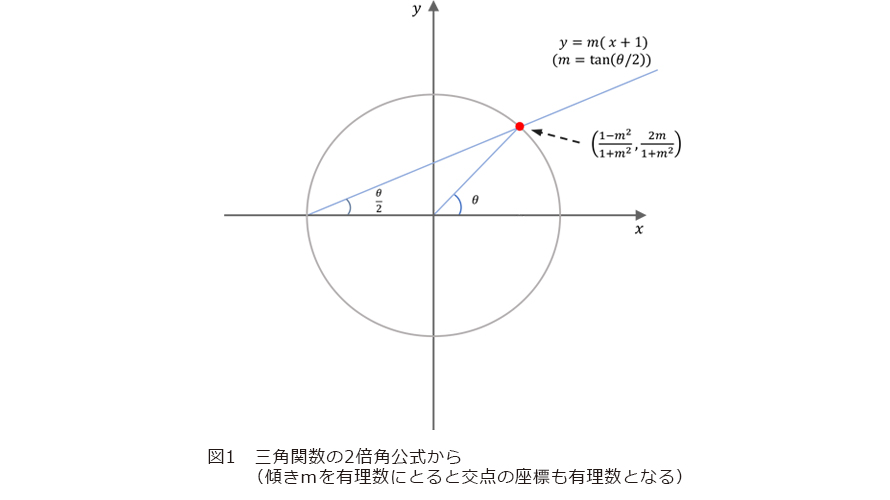
さて、与えられた方程式が有理数解を持つかどうかは、大変デリケートな問題です。![]() は座標が有理数である有理点を無限に持ちます。円と平面上
は座標が有理数である有理点を無限に持ちます。円と平面上 ![]() の点を通る傾きが
の点を通る傾きが ![]() の直線との交点を考え(三角関数の2倍角公式を利用)れば(図1)、確認は容易です。しかし、この円を少し縮めただけの円
の直線との交点を考え(三角関数の2倍角公式を利用)れば(図1)、確認は容易です。しかし、この円を少し縮めただけの円 ![]() には有理点が存在しません。微妙さといえば、
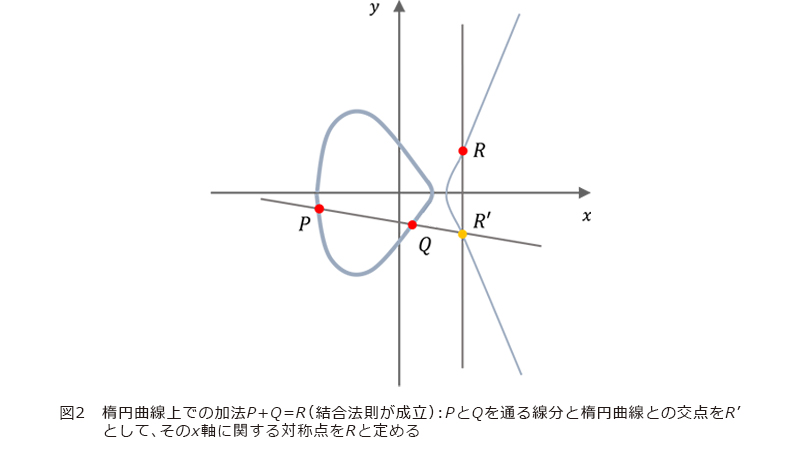
には有理点が存在しません。微妙さといえば、![]() には、自明なもの以外の有理点は存在しないというフェルマー予想(最終定理)の解決には、およそ350年を必要としました。それは、代数的視点に加え、円(加法定理により加法を積演算とするアーベル群の構造を持ちます)を越えて、楕円曲線(図2)というアーベル群の構造を持つ図形から局所的に定まるゼータ関数と(表現論(4)にかかわり)大域的に定まるゼータ関数の一致を認めるための現代数学の粋を駆使した理論なしには果たせないものでした。
には、自明なもの以外の有理点は存在しないというフェルマー予想(最終定理)の解決には、およそ350年を必要としました。それは、代数的視点に加え、円(加法定理により加法を積演算とするアーベル群の構造を持ちます)を越えて、楕円曲線(図2)というアーベル群の構造を持つ図形から局所的に定まるゼータ関数と(表現論(4)にかかわり)大域的に定まるゼータ関数の一致を認めるための現代数学の粋を駆使した理論なしには果たせないものでした。
このフェルマー予想をはじめ、数論のいくつかの問題は他の数学分野に比して問題そのものの理解は容易です。組合せ論・グラフ理論も似た特徴があります。しかもそのいくつかは、数論と表現論に深く関係していて、例えばラマヌジャングラフのような効率の良いネットワーク構成に顕著な役割を果たすものもあります。ただし、使われる手法は多岐にわたり、また非常に高度な(数式というよりは、対象を結ぶ →(矢印) を用いて述べられる多様な抽象的概念を駆使する)現代数学の飛び道具の運用が欠かせないのが普通です。そのため、多くの予想(傍証はあるが解決が困難で、種々の深い数学を巻き込む必要があると思われる言明)がなされ、いくつもが未解決のままにあります。提示後165年を経過して、いまだなお人類を寄せ付けないでいるリーマン予想や楕円曲線の構造を決めるバーチとスイナートン・ダイヤー予想は中でも有名です。また、グロタンディークの代数幾何の革新によりドリーニュにより解決されたラマヌジャン予想やヴェイユ予想は、20世紀の数論を牽引しました。フェルマー予想の鍵であった谷山-志村予想、そして非可換類体論の構築をめざすラングランズ予想は壮大な夢を与えています。しかもこれらの多くが、(明治開国後、日本でなされた世界的・歴史的成果である)類体論を含めて、生い立ちの違うゼータ関数・L関数の一致として記述されることは、特筆すべきことです。
一方で、図形上の有理点や整数点を、多項式や有理関数による反復合成が定める力学系の下で、その軌道上の有理点や整数点を調べたり、アーベル群の構造を持つ図形上の有限位数の点を周期点ととらえたりと、幾何学的性質から数論的性質を導く研究も活発です。例えば、モーデル予想(ファルティングスの定理)を含みディオファントス幾何における遥か未踏のヴォイタ予想もこうした視点の先に理解できるものかもしれません。
このように数論は貪欲です。問題解決に必要とあれば、幾何学、解析学、確率論などどんなものでも使います。幾何的インスピレーションを積極的に投入して抽象的な図形の幾何学的性質から数論的性質を導くことや、無限を精緻に取り込みつつ不変性を持つ関数をふんだんに活用すること、さらには、確率論でお馴染みの分布や密度の様子を詳細に観察するという立場から、いわゆる測度論も議論の範疇に取り込みます。その結果、研究を進める際に多くの数学分野を巻き込むことになります。ひいてはそれぞれの分野の発展に寄与することも期待できます。古くは、ベルンハルト・リーマンによる素数分布に端を発する解析数論の研究が一変数複素関数論の発展を促しました。ところで、「数学は科学の女王であり、数論は数学の女王」といったのは、19世紀最大の数学者カール・フリードリヒ・ガウスです。普通これは、数論の美しさを端的に表したのだと受け止められていますが、真意は、その美しさとともに多様な数学の使いっぷりの良さにもあるのでしょう。
本特集で取り上げる数学研究は、数論の問題を、それぞれ代数幾何、力学系の手法で探求する数論幾何、数論力学や保型形式論、また、直接・間接的に数論にかかわる表現論、数理物理、複素や ![]() 進体の力学系、組合せ論・グラフ理論、特殊関数論、微分方程式とトポロジーなどを背景にするものです。換言すれば、執筆メンバが属するNTT基礎数学研究センタは、数論の貪欲さに加えて、表現論が対称性を扱う学問として代数・幾何・解析・確率論が交差する分野であり多岐の応用があることから、その数学において、まとまりと広がりを同時に持つ研究推進組織です。
進体の力学系、組合せ論・グラフ理論、特殊関数論、微分方程式とトポロジーなどを背景にするものです。換言すれば、執筆メンバが属するNTT基礎数学研究センタは、数論の貪欲さに加えて、表現論が対称性を扱う学問として代数・幾何・解析・確率論が交差する分野であり多岐の応用があることから、その数学において、まとまりと広がりを同時に持つ研究推進組織です。
読者には、現代数学の大きな流れの一端に触れて楽しんでいただけることを願い、本特集を組みました。
数論・数論的力学系
■フェルマー予想
「この定理に関して、私は真に驚くべき証明を見つけたが、この余白はそれを書くには狭すぎる」とのコメントとともに、ディオファントスの著書「算術」の余白にピエール・ド・フェルマーが書き残した以下の問題は、書き込み入りの「算術」が刊行された1670年以降、最終的に1995年にワイルズによる証明が検証されるまでの300年以上もの間、多くの数学者の挑戦を退け続け、数論幾何の分野の発展の礎となりました。
・フェルマー予想:![]() を3以上の整数とするとき
を3以上の整数とするとき ![]() を満たす有理数の組
を満たす有理数の組 ![]() は存在しない。
は存在しない。![]() のとき方程式(1)は原点を中心とする半径1の円周を定めますが、この曲線の上には有理点(各座標が有理数であるような点)は無限にあります。さらにこれらの有理点はすべて、(-1 ,0)を通る傾きが有理数
のとき方程式(1)は原点を中心とする半径1の円周を定めますが、この曲線の上には有理点(各座標が有理数であるような点)は無限にあります。さらにこれらの有理点はすべて、(-1 ,0)を通る傾きが有理数 ![]() であるような直線との交点として実現できます(図1)。つまり、曲線の有理点が (無限大を許せば)
であるような直線との交点として実現できます(図1)。つまり、曲線の有理点が (無限大を許せば) ![]() という傾きのパラメータのみで記述できるということです。直線の傾き全体として得られる空間は射影直線と呼ばれるものです。各変数に入る値を複素数まで広げて考えると、(1)で定まる図形は実二次元、つまり曲面になります。その曲面に空いた穴の数を種数といいます。幾何的には、射影直線は種数0で滑らかな曲線のことにほかなりません。また、種数1の滑らかな曲線(と固定した点との組)のことを楕円曲線といいます。楕円曲線は複素数の範囲で考えればそれはドーナツのような見た目の図形になります(図3)。(1)で定まる曲線は
という傾きのパラメータのみで記述できるということです。直線の傾き全体として得られる空間は射影直線と呼ばれるものです。各変数に入る値を複素数まで広げて考えると、(1)で定まる図形は実二次元、つまり曲面になります。その曲面に空いた穴の数を種数といいます。幾何的には、射影直線は種数0で滑らかな曲線のことにほかなりません。また、種数1の滑らかな曲線(と固定した点との組)のことを楕円曲線といいます。楕円曲線は複素数の範囲で考えればそれはドーナツのような見た目の図形になります(図3)。(1)で定まる曲線は ![]() では楕円曲線になります。フェルマー予想は
では楕円曲線になります。フェルマー予想は ![]() のときにはフェルマー自身による無限降下法と呼ばれる方法で証明されていて、この方法は後述のモーデル-ヴェイユの定理の証明に拡張されています。
のときにはフェルマー自身による無限降下法と呼ばれる方法で証明されていて、この方法は後述のモーデル-ヴェイユの定理の証明に拡張されています。![]() のときには、数の世界を有理数全体から、1の3乗根を付け加えた数の全体に広げ、その数の世界における素因数分解の一意性を用いて証明されました。現代風にいえばこれは数体の拡大を考えていることになります。残念ながら一般の数体では素因数分解の一意性が成り立たないため、この方法を一般の
のときには、数の世界を有理数全体から、1の3乗根を付け加えた数の全体に広げ、その数の世界における素因数分解の一意性を用いて証明されました。現代風にいえばこれは数体の拡大を考えていることになります。残念ながら一般の数体では素因数分解の一意性が成り立たないため、この方法を一般の ![]() に拡張することはできませんが、このことを克服しようと見出されたクンマーの理想数の理論は現代ではイデアル論になり、体の拡大の考え方はガロア理論の基礎付けを与え、類体論を含む現代の整数論、数論幾何でも避けることはできない基礎理論の1つとなっています。
に拡張することはできませんが、このことを克服しようと見出されたクンマーの理想数の理論は現代ではイデアル論になり、体の拡大の考え方はガロア理論の基礎付けを与え、類体論を含む現代の整数論、数論幾何でも避けることはできない基礎理論の1つとなっています。![]() が5以上のときには、(1)で定まる曲線は種数2以上の曲線となります。このとき(1)の有理数解が有限個しかないことが、次の定理から従います。
が5以上のときには、(1)で定まる曲線は種数2以上の曲線となります。このとき(1)の有理数解が有限個しかないことが、次の定理から従います。
・モーデル予想(=ファルティングスの定理):有理数係数の多項式で定まる滑らかな曲線は、種数が2以上であれば有理点を有限個しか持たない。
この定理は、曲線の種数という幾何的な情報と有理点の有限性という数論的な現象とのつながりを主張する驚くべきものであり、数論幾何の分野の金字塔の1つです。この結果によりファルティングスは1986年にフィールズ賞を受賞しました。フェルマー予想については解決に至るまでまだまだたくさんの触れるべき歴史がありますが、本稿ではこれまでとします。

■楕円曲線
種数0の曲線では有理点をパラメータ付けできることは述べましたが、種数1の楕円曲線の場合にはそれほど簡単ではありません。しかし楕円曲線の場合には有理点の“足し算”を考えることができ、有理点から有理点を次々につくることができます(図2)。すなわち楕円曲線の有理点の集合は群と呼ばれる構造を持っていて、この群構造について以下が成り立ちます。
・モーデル-ヴェイユの定理:楕円曲線 ![]() の有限個の有理点
の有限個の有理点 ![]() が存在し、
が存在し、![]() の任意の有理点
の任意の有理点 ![]() は
は![]() (
( ![]() は整数、
は整数、![]() )の形にただ一通りに表すことができる。ただし
)の形にただ一通りに表すことができる。ただし
![]() はある正の整数倍で
はある正の整数倍で ![]() (すなわち任意の有理点
(すなわち任意の有理点 ![]() に対して
に対して ![]() が成り立つような元)になる点たちである。
が成り立つような元)になる点たちである。
![]() のことを楕円曲線
のことを楕円曲線 ![]() の階数といい、
の階数といい、![]() を
を ![]() のねじれ点といいます。ねじれ点の部分に制限した際の群構造はメイザーにより完全に分析されている一方で、階数については現在でも未解決な部分が多いです。ミレニアム懸賞問題の1つ、階数とL関数の極の位数との一致を見るBSD予想のみならず、任意に大きい階数の楕円曲線の存在・非存在も未解決の問題です。現在見つかっている階数の世界記録はエルキースによる、28以上であることが証明されているものです。無限か否かが問題になっているにもかかわらず、世界記録が小さいことに驚くかもしれません。
のねじれ点といいます。ねじれ点の部分に制限した際の群構造はメイザーにより完全に分析されている一方で、階数については現在でも未解決な部分が多いです。ミレニアム懸賞問題の1つ、階数とL関数の極の位数との一致を見るBSD予想のみならず、任意に大きい階数の楕円曲線の存在・非存在も未解決の問題です。現在見つかっている階数の世界記録はエルキースによる、28以上であることが証明されているものです。無限か否かが問題になっているにもかかわらず、世界記録が小さいことに驚くかもしれません。
■数論力学系
数論力学系 (arithmetic dynamics) と呼ばれる分野に属する問題自体は1950年のノースコットによる定理(射影空間の数体上定義された射は有限個しか有理周期点を持たない) などからみられますが、実際に数論力学系と呼ばれ始めたのは2000年に入ってからです。数学分野の分類コードとして用いられている 2010 Mathematics Subject Classification (MSC2010) において11S82 Non-Archimedean dynamical systems [See mainly 37Pxx]、37Pxx Arithmetic and non-Archimedean dynamical systemが追加されたタイミングで、明確に1つの分野としての地位を数学界から認められたといえます。
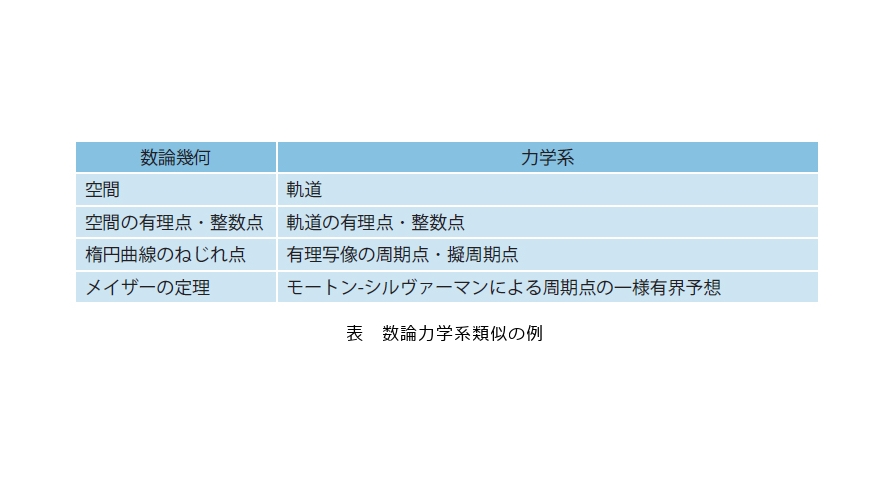
大雑把にいうと数論力学系とは、数論的に興味のある体(例えばp進数体や有理数体など)の上で、多項式や有理写像の反復合成(離散力学系)を考えたときに、有理点のふるまいなど、数論的な現象を調べる分野です。重心を数論側に置くか力学系側に置くかで問題意識は変わりますが、数論側に重心を置いた際のもう少し大きな目標としては、数論ないし数論幾何の分野で考えられているアーベル多様体に関する定理の、力学系類似(あるいは一般化)の辞書を完成させ、類似あるいは一般化された定理を与えることが挙げられます。ここで詳しく用語を説明することはできませんが、現時点で、例えば表のような類似が考えられています。
こういった、数体上の数論力学系に関する問題は本特集記事『力学系に現れる数論的課題』で詳しく紹介します。
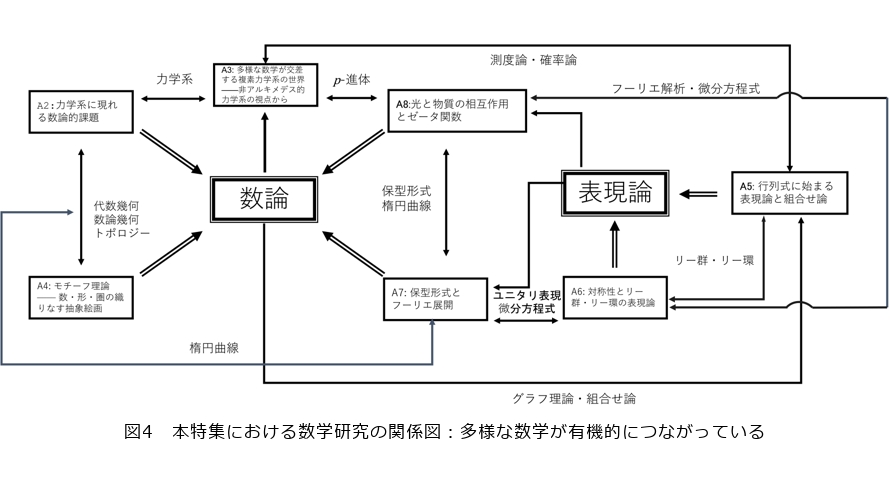
力学系側に重心を置くと、いくらか博物学的な様相を呈しているように筆者にはみえていますが、複素力学系の理論の非アルキメデス体(p進数体など)の上の力学系での類似や拡張を行う試みや、それを用いた複素力学系や数論力学系への応用は分野のメインストリームです。p進数体をはじめとする、非アルキメデス体上の力学系は本特集記事『多様な数学が交差する複素力学系の世界——非アルキメデス的力学系の視点から』(図4)で紹介されます。
最近では数論力学系に関する本やサーベイ、関連する文献の膨大なリスト(3)が作成されています。リストにある論文たちのタイトルを眺めるだけでも、新しい分野が急成長を遂げている様子を垣間見ることができるでしょう。
代数幾何・数論幾何
■方程式と幾何学
方程式の解を求めることは数学の根本的な課題です。代数学では「多項式=0」という形の方程式(代数方程式)の解を調べることが究極目標の1つです。方程式の研究において「グラフ」は非常に重要な概念です。例えば方程式 ![]() を実数の範囲で解き座標平面にプロットしてグラフを描くと、お馴染みの円が現れます。同様に、方程式
を実数の範囲で解き座標平面にプロットしてグラフを描くと、お馴染みの円が現れます。同様に、方程式 ![]() のグラフは直線になります。さらに、これら2つの方程式の共通解は、グラフの交点として図形的に表現されます(図1)。方程式の解が描く図形(グラフ)を考えることで、人間の直感が働きやすい幾何の舞台に問題を持ち込み、幾何に特有の手法を用いて問題に取り組むことができます。
のグラフは直線になります。さらに、これら2つの方程式の共通解は、グラフの交点として図形的に表現されます(図1)。方程式の解が描く図形(グラフ)を考えることで、人間の直感が働きやすい幾何の舞台に問題を持ち込み、幾何に特有の手法を用いて問題に取り組むことができます。
このような「方程式のグラフを描く」というアイデアは、1637年に刊行されたデカルトの「方法序説」で確立し、現在では初等教育で教授されるほど普及しています。しかし、上記の直感的な手法にも限界があります。実際、方程式の変数を増やすと、グラフは3次元空間内に描けなくなるため直接「目で見る」ことができなくなり、全く次元の異なる困難が現れます。このような複雑なグラフの性質を調べることを目的の1つとして、デカルト以降、多数の数学者が数世紀にわたる努力を重ねました。そうして出来上がったのが「代数幾何」という巨大な学問体系です。特に、19世紀から20世紀にかけての代数幾何の発展は、後の数学全体に影響を及ぼすほどの、非常に急激なものでした。
■代数幾何のパラダイムシフト——関数が先か、空間が先か
数学が急速に進展するとき、そこには必ず重要なパラダイムシフトが存在します。代数幾何の歴史においては「空間と関数の立場の逆転」がもっとも大きなパラダイムシフトの1つでした。
現代の数学では、幾何学的な対象を、すべて包括して「空間」と呼びます。グラフも空間の一例です。一方、関数とは空間の各点に数値を与える規則です。例えば、実数直線という空間の上には、![]() という関数が定まります。関数の値は単なる数値ですから、関数どうしの足し算、引き算、掛け算を定めることができます(割り算は、関数の値が0になり得る場合にはできません)。このように、足し算、引き算、掛け算を併せ持つ代数構造を「環(かん)」と呼びます。このように、空間という幾何的対象から出発して、環という代数的対象をつくり出せます。
という関数が定まります。関数の値は単なる数値ですから、関数どうしの足し算、引き算、掛け算を定めることができます(割り算は、関数の値が0になり得る場合にはできません)。このように、足し算、引き算、掛け算を併せ持つ代数構造を「環(かん)」と呼びます。このように、空間という幾何的対象から出発して、環という代数的対象をつくり出せます。
次に、例えば、![]() という式を考えるとどうなるでしょうか。これは逆数を対応させる式ですが、実数直線全体の上の関数にはなりません。
という式を考えるとどうなるでしょうか。これは逆数を対応させる式ですが、実数直線全体の上の関数にはなりません。![]() の逆数は存在しないためです。しかし、空間を実数直線から
の逆数は存在しないためです。しかし、空間を実数直線から ![]() を除いたものに取り替えれば、この空間の上では、
を除いたものに取り替えれば、この空間の上では、![]() は関数になっています。つまり、
は関数になっています。つまり、![]() という関数が空間の上に住んでいるなら、その空間は
という関数が空間の上に住んでいるなら、その空間は ![]() を含むことはできないわけです。
を含むことはできないわけです。
このように、空間を決めれば対応する環が決まり、逆に、環の様子を調べることで、空間の様子が分かる、という関係が見て取れます。このことを比喩的に表現すれば次のようになるでしょう。空間を「国」のようなものだと思えば、関数は「民」に相当します。国=空間があれば、そこには民=関数がいて、「+、−、×」によって民どうしが相互作用しています。しかし、国は民が集まることによって初めて形成されます。国の様子を知りたければ、どのような民が住んでいるかを調べることが有効に違いありません。
このような観察を背景として、20世紀後半に彗星のように登場したグロタンディークは、次のような素朴かつ大胆な哲学を打ち出しました。
・哲学:すべての環は、ある空間の上の関数の集まりとみなすことができる。
つまり、空間→環という対応とは逆向きの、環→空間という対応関係が存在するというのです。これは、代数方程式に対してグラフを対応させる操作の(非常に広範な)一般化になっています。実際、方程式に対して「剰余環」という環を自然に対応させることができるのですが、この環に対応する空間を考えると、方程式のグラフが復元されます(正確には、グラフよりも豊富な情報を持つ「代数多様体」が得られます)。
グロタンディークはこの哲学を数学的に精密な理論として結実させることに成功しました。「スキーム理論」と呼ばれるこの理論は、それまでの代数幾何の枠組みを根底から書き換える壮大なもので、その基礎付けを行った著作は数千ページに及びます。また、理論の構築の過程では、20世紀に発達した圏、関手といった抽象数学が本質的に、縦横無尽に用いられます。
■数論幾何
グロタンディークがスキーム理論をつくり上げた動機は、数論への応用にありました。環のもっとも素朴な例は、整数をすべて集めた集合です。整数どうしに「+、−、×」を行っても再び整数ですから、確かに環になっています。これを「整数環」と呼びます。整数環の性質を明らかにすることが数論の究極目標の1つです。スキーム理論により、整数環に対しても空間が自然に対応し、これを通じて数論の問題を自然に幾何学の問題に翻訳することができます。このように、スキーム理論を用いて数論を研究する分野を数論幾何と呼びます。数論幾何については、本特集記事『モチーフ理論——数・形・圏の織りなす抽象絵画』でさらに詳しく触れます。
スキーム理論を用いると、整数に限らず、情報分野で扱われる1+1=0が成り立つような数の体系(正標数の環)を含む、直感的でない数の世界においてすら、幾何を考えることが可能になります。現在では、正標数の世界の代数多様体(楕円曲線など)は情報・暗号分野において重要な役割を演じています。純粋に数論的な興味から出発し、抽象数学の力をフル活用して発展した代数幾何・数論幾何が、実社会における具体的な応用の不可欠な理論的支柱となっているという事実は驚くべきことです。
数論幾何は代数・幾何・解析と複雑に絡み合いながら成長し、現在では、数論研究の巨大な大動脈となっています。面白いことに、純粋に数学的な好奇心から発生した数論幾何は、数論とは(一見)遠く離れたさまざまな領域に転用可能な概念を生み出し、予期されていなかった応用をもたらしています。例えば、ヴェイユ予想の解決で鍵となった代数多様体の「重さ」の理論は、理論物理の最先端にあたる弦理論やミラー対称性の研究において不可欠な基盤となっています。また上述のように、フェルマー予想の証明でも重要な役割を演じる楕円曲線は、耐量子暗号の構成や認証技術をはじめとして、情報理論でも幅広く応用されています。数論幾何は(数学の歴史全体でみれば)まだ若く、現在でも新たなイノベーションが起き続けている分野です。これからも数学の内外に予期せぬ果実をもたらし続けることでしょう。
表現論と保型形式
■群の作用
表現論と聞いて数学者が真っ先に考えることは、群が何かに作用している状況です。さらに群といえば、20歳で決闘により亡くなったエヴァリスト・ガロアの名が浮かびます。「五次以上の方程式には一般的な代数解(四則演算と冪根で表示できる解)の公式がない」というアーベル-ルフィニの定理の証明を大幅に簡略・普遍化し、与えられた方程式がいつ代数的な解の表示を持つかについて、群概念の先駆けを用いて特徴付けました。いわゆるガロア理論です。ガウスによる平方剰余の相互法則を起源に、「クロネッカーの青春の夢」を実現することで代数的整数論の金字塔を打ち立てた高木貞治の類体論もガロア理論が元にあります。それはまた、今や非可換類体論に向けたラングランズ予想と呼ばれる壮大な理論体系の柱ともいえます。一方で、群の定義そのものはあっさりしており ①「積」なる二項演算が定義されていて、それが結合法則を満たし、②単位元が存在し、③各元に逆元が存在する、というものです。
有限群でいえば、身近にある正多面体群、結晶群、行列式の定義に現れる対称群のほか、有限次元ベクトル空間V上の正則(逆行列を持つ)線型変換たちがなす一般線型群GL(V)などがあります。ルービックキューブの目をそろえるための一連の操作も、「手」が物理的な群演算を施していると考えられます。
■群の表現論
一方表現論というと、文学ですか、あるいは数学分野にそのようなものがあるのですか、と問われることがあります。20世紀初頭にドイツで生まれた芸術運動に端を発する表現主義の影響です。それは一般に、感情を作品中に反映させて表現する傾向を指していて、英語では 「expressionism」です。他方、表現論は「representation theory」です。表現論(特に群の表現論)とは、群の各元をベクトル空間Vの線型変換として表現することでそれが作用するVを研究する数学の一分野です。表現論が独立した研究対象となった歴史的契機は、デデキントがフロベニウスに宛てた1886年の書簡における群行列式の因数分解の問題です。有限群の指標の理論はここに始まりました。指標とは表現(行列)のトレースです。指標により表現が本質的に決まることもポイントです。また、ソフィス・リーは微分方程式に対するガロア理論の構築をねらい現在のリー環・リー群を創始する研究を行いました(4)。ただし、これらの表現は、Vとして無限次元空間を考察することが重要ですが、その場合には位相も考えます。しかし、現代の表現論の発展を決定的に進歩させたのは、「相対論」と「量子力学」という物理学における革命的理論と、ラングランズ予想に至る道中で飛躍的な進歩を遂げている数論研究です。技術面に限れば、群や環などの代数系に依存してやや異なりますが、表現論の目標は以下の3つに集約・大別されます。
・素数のような基本的役割を果たす既約表現の構成と分類(もれなく重複がないリストをつくること)
・与えられた表現を、既約表現の「和」として分解すること(困難の分割)
・同じ表現でもさまざまなカオを持ちます(同値な表現)。そのさまざまなカオ(同値類の各元)を、例えば興味深い幾何学的対象を用いて構成すること(応用上の有益)
どうして単純に見える行列群のような群を難しい線型変換として表現するのか、などの疑問を持つ方もいらっしゃるでしょう。しかしそれは、むしろ逆です。大変複雑に見えるものでも、正しく解きほぐせば(分解)、1つひとつは単純(易しい群の作用)だと分かり、その結果、対象の真の理解に到達できるというわけです。これらの研究には、微分方程式、関数解析、特殊関数論や組合せ論(5)、そしてガロア以来相性の良い圏論などが駆使されることになります。
■保型形式
現在では純代数的に語られることが多いラングランズ予想ですが、そのアイデアの原点はセルバーグによる非正則なアイゼンシュタイン級数の解析接続の理論とハリッシュチャンドラの壮大なリー群の表現論の研究にありました。実際、表現論は、純代数的に定式化されている数論の疑問の解決のために、それをフーリエ変換や ![]() 級数などの解析的なものに置き換えて研究する際に果たす強固な架け橋です。そこには、連続群や離散群の自然な作用が背後にあり、それらによる不変性の記述が問題を明確化しています。例えば、フェルマーの最終定理の後、その何倍も難しいとされていた佐藤-テイト予想(の一部)が、2011年にリチャード・テイラーたちにより解決されました。20世紀の数論を牽引したラマヌジャン予想とは、楕円曲線の
級数などの解析的なものに置き換えて研究する際に果たす強固な架け橋です。そこには、連続群や離散群の自然な作用が背後にあり、それらによる不変性の記述が問題を明確化しています。例えば、フェルマーの最終定理の後、その何倍も難しいとされていた佐藤-テイト予想(の一部)が、2011年にリチャード・テイラーたちにより解決されました。20世紀の数論を牽引したラマヌジャン予想とは、楕円曲線の ![]() 関数の零点の絶対値分布がリーマン予想の類似を満たすことでしたが、それはさらに、零点の偏角分布が
関数の零点の絶対値分布がリーマン予想の類似を満たすことでしたが、それはさらに、零点の偏角分布が ![]() 分布するという、1963年に佐藤幹夫により定式化された予想です。その難しさは、フェルマー予想では一個の
分布するという、1963年に佐藤幹夫により定式化された予想です。その難しさは、フェルマー予想では一個の ![]() 関数で収まっていた問題を、
関数で収まっていた問題を、![]() 個の対称積
個の対称積 ![]() から定まる表現に付随する
から定まる表現に付随する ![]() 関数に対して解決せねばならないからでした。この解決は極めて画期的なものですが、より重大な多くの未解決部分が残されています。佐藤-テイト予想への挑戦はラングランズ予想攻略の核心にもあたり、その解決には、表現論に深くかかわる非正則な保型形式の研究の進歩が待たれています(6)。本特集で紹介される保型表現と表現論の2つの記事は、その根幹にかかわる研究です。他方、表現論と量子力学の関係は深く数論研究にも及びます。またそれは、不変式論、組合せ論や確率論・統計学の問題にも深くつながるものです。これらについても、その一端を本特集の記事の中で紹介します。
関数に対して解決せねばならないからでした。この解決は極めて画期的なものですが、より重大な多くの未解決部分が残されています。佐藤-テイト予想への挑戦はラングランズ予想攻略の核心にもあたり、その解決には、表現論に深くかかわる非正則な保型形式の研究の進歩が待たれています(6)。本特集で紹介される保型表現と表現論の2つの記事は、その根幹にかかわる研究です。他方、表現論と量子力学の関係は深く数論研究にも及びます。またそれは、不変式論、組合せ論や確率論・統計学の問題にも深くつながるものです。これらについても、その一端を本特集の記事の中で紹介します。
■参考文献
(1) 初田・柴藤:“数理の窓から世界を読みとく:素数・AI・生物・宇宙をつなぐ,”岩波ジュニア新書,2021.
(2) 山崎・新井・小林・斎藤・吉田:“初等整数論 —数論幾何への誘い—(共立講座 数学探検 6),”共立出版,2015.
(3) https://web.archive.org/web/20080513023708/http://www.math.brown.edu/~jhs/ADSBIB.pdf
(4) 平井・山下:“表現論入門セミナー:具体例から最先端にむかって,”日本評論社,2003.
(5) フルトン・ハリス(木本訳):“フルトン-ハリスの表現論入門(上下),”丸善出版,2024.
(6) コブリッツ・上田:“楕円曲線と保型形式,”丸善出版,2012.

(左から)佐野 薫/宮﨑 弘安/若山 正人







多くの応用を生み出している数学の基礎研究の多くは、数学者の純粋な好奇心から生み出されてきました。本特集をとおして現代数学の歩みと、私たちが数学にかける想い、そして数学の発展の最前線の一端をお伝えできればと思います。