2024年7月号
特集
力学系に現れる数論的課題
- 数論
- 力学系
- Diophantus幾何
離散力学系の分野では、ある種の図形の変換(自己写像)が与えられたとき、その変換を反復して施すときの各点の漸近挙動を理解することが究極的な目標です。数論力学系の分野においては、特に数論的に興味を持たれる値(代数的数や ![]() 進数)を座標に持つ点の漸近挙動が調べられています。こうしたものの研究に関連して、曲線の有理点決定問題に帰着される課題群があります。本稿では数論力学系におけるこれらの課題の問題意識について紹介します。
進数)を座標に持つ点の漸近挙動が調べられています。こうしたものの研究に関連して、曲線の有理点決定問題に帰着される課題群があります。本稿では数論力学系におけるこれらの課題の問題意識について紹介します。
佐野 薫(さの かおる)
NTT基礎数学研究センタ
はじめに
時間経過に沿って各点がある規則に従って動いていく系のことを力学系といいます。ある多項式ないしは有理関数 ![]() が与えられたとき、その反復合成による各点の軌道、つまり
が与えられたとき、その反復合成による各点の軌道、つまり

という数列を考え、この反復合成の回数を離散的な時刻とみなすと、力学系が得られます。これがいつ無限大に発散するのか、いつ何かの値に収束するのか、というのは初歩的でありつつ難しい問いです。数論力学系とは、こうした力学系に現れる数論的現象を調べる分野であり、シルヴァーマンにより2000年前後に生まれた比較的新しい分野です。数論と力学系のどちら寄りに問題意識の重心を置くかによって、研究にはグラデーションがあります。本稿では数論寄りの問題意識でみた数論力学系について、特に何らかの曲線の有理点の決定問題に関連する問題群について紹介します。力学系寄りの問題意識でみた数論力学系については、本特集記事『多様な数学が交差する複素力学系の世界――非アルキメデス的力学系の視点から』で紹介します。
数論力学系の1つの大きな問題意識は、数論幾何とりわけ楕円曲線やその高次元版であるアーベル多様体の理論の、力学系での類似の辞書を埋めること、ないしはその類似を通じて、数論幾何の新たな知見を得ることにあります。
モートン-シルヴァーマン予想
楕円曲線のねじれ点とは、自分自身を(楕円曲線に定まっている加法で)何度か足すとOになるような点のことです。これは、2倍するという写像を反復して施して得られる軌道が有限集合になるような点、ということと同じことです。楕円曲線が有理数体上で定義されている場合には、このような有理点の個数が16個以下であること(より正確には、群構造のあり得るパターンの完全決定)がメイザーにより証明されています。では例えば、実数の直線上の ![]() という写像の反復ではどうでしょうか。
という写像の反復ではどうでしょうか。 ![]() による軌道が有限になるものは複素数の範囲では1のべき乗根たちと0です。このうち有理数(有理擬周期点)は0、1、−1の3つのみです。
による軌道が有限になるものは複素数の範囲では1のべき乗根たちと0です。このうち有理数(有理擬周期点)は0、1、−1の3つのみです。![]() という写像ではどうでしょうか。この場合の有理擬周期点は実は
という写像ではどうでしょうか。この場合の有理擬周期点は実は ![]() の4つのみです。有理擬周期点が有限個なのは、これらの写像が特殊だからなのでしょうか。実際はそうではありません。有理数係数の
の4つのみです。有理擬周期点が有限個なのは、これらの写像が特殊だからなのでしょうか。実際はそうではありません。有理数係数の ![]() 次多項式(
次多項式( ![]() )に対しても有理擬周期点の個数が有限個であることが証明できます。ではその個数は上で挙げたように3個、4個程度で収まるのでしょうか。軌道が有限であるだけでなく、周期的な軌道を持つ有理点(有理周期点)に制限すると、どんな周期があり得るでしょうか。それに答えるのが次の予想です。
)に対しても有理擬周期点の個数が有限個であることが証明できます。ではその個数は上で挙げたように3個、4個程度で収まるのでしょうか。軌道が有限であるだけでなく、周期的な軌道を持つ有理点(有理周期点)に制限すると、どんな周期があり得るでしょうか。それに答えるのが次の予想です。
・モートン-シルヴァーマンの一様有界性予想 (の特殊な場合):2以上の整数 ![]() に対し定数
に対し定数 ![]() があり。有理数係数の
があり。有理数係数の ![]() 次有理式
次有理式 ![]() の有理擬周期点の個数は
の有理擬周期点の個数は ![]() 個以下である。
個以下である。
この予想は2次多項式 ![]() (
( ![]() は与えられた有理数)の場合に限っても広く未解決です。周期が1、2、3の有理周期点
は与えられた有理数)の場合に限っても広く未解決です。周期が1、2、3の有理周期点 ![]() があるような
があるような ![]() が無限にあることは比較的容易に証明できる一方、周期4、5、6の周期有理点を持つような有理数
が無限にあることは比較的容易に証明できる一方、周期4、5、6の周期有理点を持つような有理数 ![]() は存在しないことが示されています。ただし周期が6のものについてはBSD(バーチ-スウィンナートン-ダイアー)予想の仮定を必要としているのが現状です。また、
は存在しないことが示されています。ただし周期が6のものについてはBSD(バーチ-スウィンナートン-ダイアー)予想の仮定を必要としているのが現状です。また、 ![]() 予想をさらに一般化した予想を仮定すれば、
予想をさらに一般化した予想を仮定すれば、 ![]() は周期4以上の周期有理点を持たないことが証明されています。周期
は周期4以上の周期有理点を持たないことが証明されています。周期 ![]() の有理周期点を探すということを考えたとき、勘の良い方であれば、
の有理周期点を探すということを考えたとき、勘の良い方であれば、 ![]() としたとき
としたとき ![]() 回反復合成を考え、
回反復合成を考え、 ![]() という方程式を解くというアイデアを思いつくかもしれません。より精密には、例えば
という方程式を解くというアイデアを思いつくかもしれません。より精密には、例えば ![]() = 4 のときには周期2の周期有理点もこれを満たしてしまいます。それを反映して、
= 4 のときには周期2の周期有理点もこれを満たしてしまいます。それを反映して、![]() を
を ![]() で割って得られる(
で割って得られる( ![]() 、
、 ![]() に関する)多項式の解を考えればよいでしょう。一般の周期
に関する)多項式の解を考えればよいでしょう。一般の周期 ![]() に対しても同様です。このようにして得られる多項式は
に対しても同様です。このようにして得られる多項式は ![]() 次力学系的多項式(Dynatomic polynomial)と呼ばれます。Dynatomicというのは円分多項式(Cyclotomic polynomial)の力学系バージョンとして考えられた造語です。さて、
次力学系的多項式(Dynatomic polynomial)と呼ばれます。Dynatomicというのは円分多項式(Cyclotomic polynomial)の力学系バージョンとして考えられた造語です。さて、 ![]() 次力学系的多項式は
次力学系的多項式は ![]() 、
、 ![]() に関する多項式ですが、これにより定まる図形
に関する多項式ですが、これにより定まる図形 ![]() は曲線になり、曲線の有理点(
は曲線になり、曲線の有理点( ![]() ,
, ![]() )の有無を問う問題になります。このような問題、すなわち曲線族の有理点の有無に関する問題を読者の方々はご存じでしょう。そう、フェルマー予想です。実際上で述べた
)の有無を問う問題になります。このような問題、すなわち曲線族の有理点の有無に関する問題を読者の方々はご存じでしょう。そう、フェルマー予想です。実際上で述べた ![]() =4,5,6のいずれの場合もフェルマー予想解決に至るまでに構築された、具体的な曲線の有理点決定に関する理論をフルに使って証明されています。ただしここで注意したいのが、フェルマー予想解決の決定打となった理論は、具体的な曲線の有理点決定の各論ではないということです。フェルマー予想の非自明な有理数解を用いて、フライ曲線と呼ばれる非常に性質が良い楕円曲線が定義されます。現在では定理となっている谷山-志村予想によると、任意の楕円曲線がある保型形式に対応します。ところが、元の楕円曲線の性質の良さから、対応する保型形式の性質が良くなりすぎ、実際にはそのようなものが存在しないことが証明され矛盾し、フェルマー予想の非自明な解がないということが帰結されるのでした。
=4,5,6のいずれの場合もフェルマー予想解決に至るまでに構築された、具体的な曲線の有理点決定に関する理論をフルに使って証明されています。ただしここで注意したいのが、フェルマー予想解決の決定打となった理論は、具体的な曲線の有理点決定の各論ではないということです。フェルマー予想の非自明な有理数解を用いて、フライ曲線と呼ばれる非常に性質が良い楕円曲線が定義されます。現在では定理となっている谷山-志村予想によると、任意の楕円曲線がある保型形式に対応します。ところが、元の楕円曲線の性質の良さから、対応する保型形式の性質が良くなりすぎ、実際にはそのようなものが存在しないことが証明され矛盾し、フェルマー予想の非自明な解がないということが帰結されるのでした。
モートン-シルヴァーマンの予想についてもこの驚きの方法が適用できないかと模索するのは自然なことですが、フライ曲線を定めるような方法は全く見出されていないのが現状です。
また、楕円曲線のねじれ有理点の個数が16個以下であることはすでに紹介したとおりですが、加法が定義されたより高次元の空間(アーベル多様体)についてはどうかというと、これは二次元の場合においてすら未解決問題です。実はファクルディンにより、この予想がモートン-シルヴァーマン予想から従うことが証明されており、単に類似を辿るということを超えた意義があるわけです。
力学系的消去
モートン-シルヴァーマン予想に関連して、次のようなシチュエーションを考えてみましょう。![]() を次数が
を次数が ![]() の多項式とします。仮に
の多項式とします。仮に ![]() が擬周期有理点 (軌道が有限集合であるような点)
が擬周期有理点 (軌道が有限集合であるような点)![]() を持っているとします。このような点は何度か
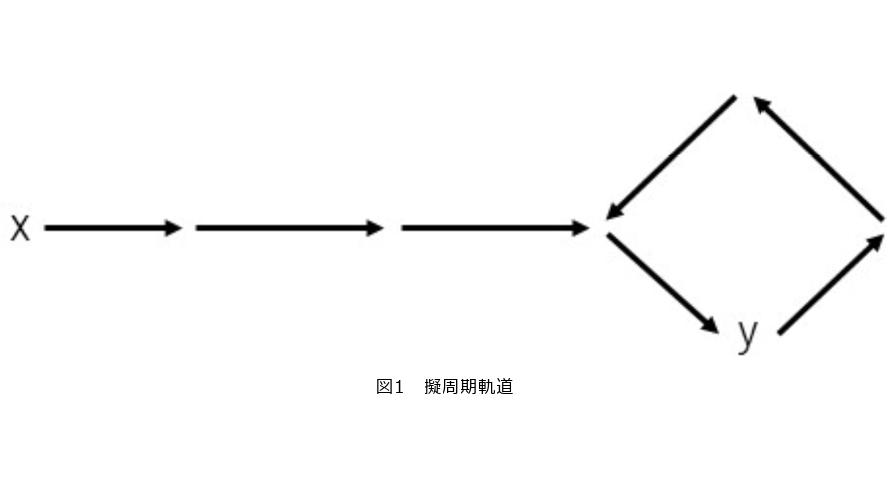
を持っているとします。このような点は何度か![]() で送ると周期軌道に入ることが分かります。仮に時刻3で周期4の周期軌道に乗ったとしましょう。つまり図1のような、周期4の周期軌道に長さ3の“尻尾”が付いている状況です。このとき
で送ると周期軌道に入ることが分かります。仮に時刻3で周期4の周期軌道に乗ったとしましょう。つまり図1のような、周期4の周期軌道に長さ3の“尻尾”が付いている状況です。このとき ![]() とすると
とすると ![]() と
と ![]() は時刻3で初めて衝突します。つまり
は時刻3で初めて衝突します。つまり ![]() および
および ![]() が成り立つということです。一般に
が成り立つということです。一般に ![]() を固定したとき、このような現象
を固定したとき、このような現象 ![]() かつ
かつ ![]() が起こるような有理点の組(
が起こるような有理点の組( ![]() ,
, ![]() )はどのくらいあるでしょうか。どれだけ大きな
)はどのくらいあるでしょうか。どれだけ大きな ![]() についてもこのような(
についてもこのような( ![]() ,
, ![]() )は存在するでしょうか。この問いは力学系的消去と呼ばれています。この問いに答えるためには、例えば整数
)は存在するでしょうか。この問いは力学系的消去と呼ばれています。この問いに答えるためには、例えば整数 ![]() (
( ![]() ≥ 1 )ごとに
≥ 1 )ごとに
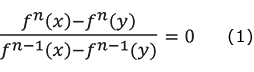
で定まる方程式の解( ![]() 、
、![]() )の有無を調べればよいでしょう。
)の有無を調べればよいでしょう。
これもやはり ![]() 、
、![]() を変数とみなすと曲線の有理点決定問題になっており難しそうですが、実はこれについては2023年 ベルー松澤‒サトリアーノにより、次数2以上の任意の有理写像
を変数とみなすと曲線の有理点決定問題になっており難しそうですが、実はこれについては2023年 ベルー松澤‒サトリアーノにより、次数2以上の任意の有理写像 ![]() について、十分大きな
について、十分大きな ![]() をとると
をとると ![]() かつ
かつ ![]() が成り立つような有理点の組(
が成り立つような有理点の組( ![]() ,
, ![]() )が存在しないことが証明されています。た、執筆者と松澤の共同研究により、これを二次元に一般化した結果が得られているほか、チョンはさらに高次元化した結果を得ています。これらの結果は曲線の有理点決定問題ではあるものの、その証明はいずれも代数幾何や
)が存在しないことが証明されています。た、執筆者と松澤の共同研究により、これを二次元に一般化した結果が得られているほか、チョンはさらに高次元化した結果を得ています。これらの結果は曲線の有理点決定問題ではあるものの、その証明はいずれも代数幾何や ![]() 進数を用いた解析によるものです。
進数を用いた解析によるものです。
こうした高次元化とは別の方向ですが、次数 ![]() を固定したとき、力学系的消去に現れる
を固定したとき、力学系的消去に現れる ![]() の限界は
の限界は ![]() によらずに決まるのか、など、一様性についても興味深いところで、もしこの“一様版力学系的消去”が成り立てば、前述したような例を考えることで、擬周期軌道の尻尾の長さの限界を知ることができ、モートン-シルヴァーマン予想への貢献が見込まれます。
によらずに決まるのか、など、一様性についても興味深いところで、もしこの“一様版力学系的消去”が成り立てば、前述したような例を考えることで、擬周期軌道の尻尾の長さの限界を知ることができ、モートン-シルヴァーマン予想への貢献が見込まれます。
Oの逆像
改めて楕円曲線の話に戻って、![]() べき倍してOになるようなねじれ点がどのくらいあるかという問題を考えてみましょう。ここで
べき倍してOになるようなねじれ点がどのくらいあるかという問題を考えてみましょう。ここで ![]() は素数です。これはねじれ点全体の個数よりかなり少ないわけですが、もし有限個以外の
は素数です。これはねじれ点全体の個数よりかなり少ないわけですが、もし有限個以外の ![]() でこのようなねじれ点がO以外にないことが示せれば、それはメイザーの定理に匹敵する結果を従います。もちろん同様のことはアーベル多様体でも考えられます。さてここで、
でこのようなねじれ点がO以外にないことが示せれば、それはメイザーの定理に匹敵する結果を従います。もちろん同様のことはアーベル多様体でも考えられます。さてここで、![]() べき倍してOになるような点とは、
べき倍してOになるような点とは、![]() 倍写像を何度か施すとOになる点ということにほかなりません。このような点の存在・非存在についての問題の力学系における類似問題を先ほどの例
倍写像を何度か施すとOになる点ということにほかなりません。このような点の存在・非存在についての問題の力学系における類似問題を先ほどの例 ![]() で考えてみましょう。すなわち、
で考えてみましょう。すなわち、![]() となる有理数の組(
となる有理数の組( ![]() ,
, ![]() )と正の整数
)と正の整数 ![]() はどのくらいあるでしょうか。これは
はどのくらいあるでしょうか。これは ![]() で定まる曲線
で定まる曲線 ![]() の有理点の決定問題そのものですが、フェイバー-ハッツ-ストールによりBSD予想の仮定の下、
の有理点の決定問題そのものですが、フェイバー-ハッツ-ストールによりBSD予想の仮定の下、![]() ≥ 4 では
≥ 4 では ![]() ≠ –1,0 なる有理点(
≠ –1,0 なる有理点( ![]() ,
, ![]() )が存在しないことが証明されています。
)が存在しないことが証明されています。![]() の点(
の点( ![]() ,
, ![]() )を
)を ![]() の(
の( ![]() ,
, ![]() )に送る写像により曲線どうしが深くかかわり合っていることは特筆すべき性質であり、楕円曲線のねじれ点を記述する曲線(モジュラー曲線)との類似点となっています。
)に送る写像により曲線どうしが深くかかわり合っていることは特筆すべき性質であり、楕円曲線のねじれ点を記述する曲線(モジュラー曲線)との類似点となっています。
樹状ガロア表現
曲線の有理点決定問題から少し方向を変えて、数体の拡大に関する問題を紹介します。フェルマー予想へのクンマーのアプローチにみられるように、一般に数の世界を拡大したとき(すなわち数体を考えたとき)素因数分解の一意性の成否は非常に重要な問題です。素因数分解の一意性の成り立たない程度を記述する量として、類数というものがあります。数体が与えられたとき、その類数を計算するのは現代でも非常に難しい中心的な問題の1つです。
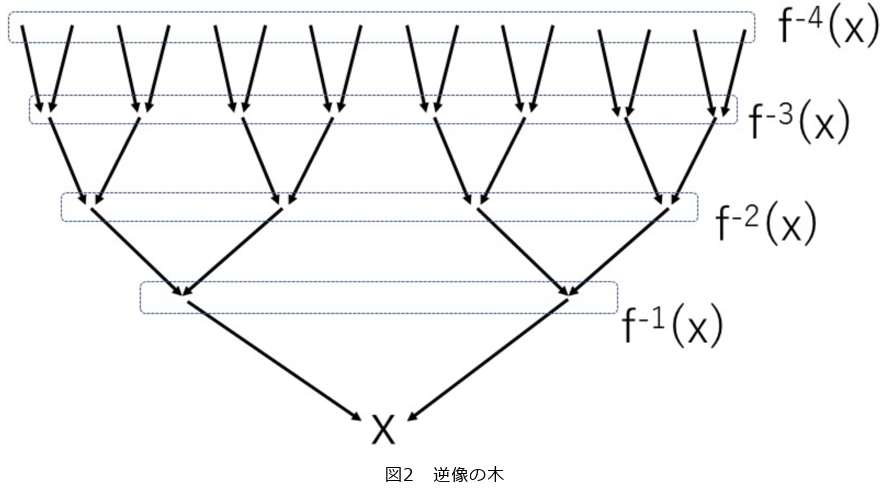
それでは、数論の重要定理である岩澤理論の類推としての数論力学系の問題をみてみましょう。多項式 ![]() および有理数
および有理数 ![]() を固定し、その
を固定し、その ![]() の反復合成による逆像たちからなる樹状の点列を考えます(図2)。この木に含まれる有理点の個数の問題について前述しましたが、大抵の場合は早い段階で有理数ではなくなってしまうのでした。それらを有理数体に付け加えて得られる数体を反復ガロア拡大と呼びます。反復ガロア拡大は反復回数を増やしていくと、どのように変化していくでしょうか。例えば
の反復合成による逆像たちからなる樹状の点列を考えます(図2)。この木に含まれる有理点の個数の問題について前述しましたが、大抵の場合は早い段階で有理数ではなくなってしまうのでした。それらを有理数体に付け加えて得られる数体を反復ガロア拡大と呼びます。反復ガロア拡大は反復回数を増やしていくと、どのように変化していくでしょうか。例えば ![]() として1の逆像を考えてみましょう。これは1の
として1の逆像を考えてみましょう。これは1の ![]() べき乗根をすべて考えることに相当し、これらをすべて有理数体に付け加えると、円分
べき乗根をすべて考えることに相当し、これらをすべて有理数体に付け加えると、円分 ![]() 拡大と呼ばれるものが得られます。さて、円分
拡大と呼ばれるものが得られます。さて、円分 ![]() 拡大を
拡大を ![]() 段階目までで止めると数体が得られますが、岩澤理論の一部として、岩澤類数公式と呼ばれるものがあり、類数の漸近挙動が記述できます。これ自体驚くべき定理ですが、では円分
段階目までで止めると数体が得られますが、岩澤理論の一部として、岩澤類数公式と呼ばれるものがあり、類数の漸近挙動が記述できます。これ自体驚くべき定理ですが、では円分 ![]() 拡大の代わりに、例えば
拡大の代わりに、例えば ![]() による
による ![]() の逆像を考えたときの反復ガロア拡大について、類数はどのように振る舞うでしょうか。岩澤類数公式のような、類数の漸近公式はあるでしょうか。岩澤理論においては、類体論が基本的な道具として用いられており、ガロア群(数体のある種の対称性を記述する群)が可換であることは必要不可欠な仮定です。しかし多くの場合には反復ガロア拡大のガロア群は非可換群であり、木の図形の対称性(自己同型群)の大部分を実現することが期待されています。円分
の逆像を考えたときの反復ガロア拡大について、類数はどのように振る舞うでしょうか。岩澤類数公式のような、類数の漸近公式はあるでしょうか。岩澤理論においては、類体論が基本的な道具として用いられており、ガロア群(数体のある種の対称性を記述する群)が可換であることは必要不可欠な仮定です。しかし多くの場合には反復ガロア拡大のガロア群は非可換群であり、木の図形の対称性(自己同型群)の大部分を実現することが期待されています。円分 ![]() 拡大では全く逆に木の対称性のほとんどを実現しないのですが、これは非常に珍しい状況であるということです。木の対称性の多くを実現しない場合(つまり木の自己同型群の中でガロア群が無限指数である場合)には、考えている多項式
拡大では全く逆に木の対称性のほとんどを実現しないのですが、これは非常に珍しい状況であるということです。木の対称性の多くを実現しない場合(つまり木の自己同型群の中でガロア群が無限指数である場合)には、考えている多項式 ![]() が力学系的に何か特別な性質を持っていると考えられており、例えば力学系が自己同型を持つ場合、臨界点がすべて擬周期点である場合、複数の臨界点の軌道が交わる場合などでは実際に無限指数になることが知られています。しかしこれらで無限指数になる状況が尽くされているのかについては未解決の問題です。こうした問題を解決していくことは、岩澤理論の非可換化という大課題へのアプローチの1つになるでしょう。
が力学系的に何か特別な性質を持っていると考えられており、例えば力学系が自己同型を持つ場合、臨界点がすべて擬周期点である場合、複数の臨界点の軌道が交わる場合などでは実際に無限指数になることが知られています。しかしこれらで無限指数になる状況が尽くされているのかについては未解決の問題です。こうした問題を解決していくことは、岩澤理論の非可換化という大課題へのアプローチの1つになるでしょう。
おわりに
多項式や有理式の反復合成から生じる数論の問題をいくつか紹介してきましたが、それらは楕円曲線やアーベル多様体の理論、岩澤理論の類似であるだけにとどまらず、複素力学系の技術の拡張や、新たな数論的な現象を明らかにしていくものです。数論力学系はまだまだ若い分野ですが、代数幾何、複素力学系、数論幾何など、さまざまな分野の研究者を巻き込み、めざましいスピードで発展しています。ぜひ、これからの研究にご期待ください。

佐野 薫







工夫なくコンピュータで扱えるのは有限桁の小数、したがって有理数です。何かのアルゴリズムを走らせて状態を推移させていくとき、それはすでに数論力学系の範疇かもしれません。読者の皆様の身近なものにも、実は数論力学系の研究対象が潜んでいるかもしれません。