2020年9月号
特集
量子情報処理における量子的間接制御の可能性
- 量子コンピュータ
- 量子的間接制御
- ノイズ
近年、量子コンピュータや量子暗号など量子と名の付く話題を目にする機会が増えています。これら量子情報処理を実現できれば、通常のコンピュータで解けない問題が解けたり、絶対に秘密が守られる暗号が実現できたりします。しかし、その実現にはまだ越えなければならない山も存在します。本稿では、その山を越えるための手段の1つとして、量子的間接制御という手段を紹介するとともに、量子情報処理を実現する手段として量子的間接制御が有用な性質を持っていることが発見されたことを示します。
加藤 豪(かとう ごう)
NTTコミュニケーション科学基礎研究所
量子情報処理の現状
量子情報処理の1つである量子コンピュータは、2つの状態が同時に存在できるという量子力学の性質を利用した計算機であり、並列の処理が自然にできる計算機です。その結果、現在使われているどんな暗号も容易に解読するなど、現在のコンピュータでは不可能とされることができるようになります。それ故に、量子コンピュータの実装が大きく期待されているところです。また、量子情報処理のもう1つとして、量子暗号がありますが、同時に計ることができない量があるという量子力学の性質を利用した暗号であり、原理的に安全な暗号です。量子暗号は、従来使われている現代暗号の欠点を補完する要素として期待されています。
実用化という面において、量子暗号が実装された装置はすでに開発されています。こういった装置は現時点では一般に販売されているわけではないものの、特殊な場合であれば実社会に導入されるのも時間の問題でしょう。実際、中国・EU・米国においては、量子暗号の実機を使ったフィールド実験の研究が国家主導で盛んに行われています。
他方、量子コンピュータの実用化への道のりはまだ今少し遠い状況です。Googleがつくった量子コンピュータが従来のコンピュータを凌駕することを示したという記事や、IBMがクラウド上で量子コンピュータを使うサービスを始めたという話題などを目にした方もいらっしゃるかもしれません。実際、数十量子ビットの量子コンピュータはすでに実現されています。しかし、社会のありかたを変えることができるほどの規模・精度の量子コンピュータにまでにはなっていません。例えば、現在インターネット上でまさに使われている暗号を解読するためには、ノイズが全くない理想的な量子コンピュータであっても数千量子ビット、ノイズがわずかに残っているものならば、数百万量子ビット必要です。つまり、現在の量子コンピュータの規模は、社会に影響を与えるにはまだ桁違いに小さいことがお分かりいただけるでしょう。
量子コンピュータの規模を大きくするには現在2つの解決すべき問題点が存在します。1つはノイズの増大です。いかに小規模なシステムであろうと、量子コンピュータにおいてノイズを完全に除去することは現在できていません。そして、量子コンピュータの規模が大きくなればなるほど、ノイズの影響は大きくなっていきます。そのため規模を大きくしてもノイズの影響を増加させない手立てを見つけ出す必要があります。量子誤り訂正符号はこの問題を解決する1つの有力な手段であり、現在もよく研究されていますが、実用できるまでにはなっていません。もう1つの問題は、大規模な量子コンピュータを制御するのに必要な制御機構は現実的には実装困難な点です。通常の量子コンピュータのモデルにおいては、その量子コンピュータを構成する量子ビットの数に比例する数の制御機構が必要です。つまり、量子コンピュータが大規模となり量子ビットの数も増大するに従って、膨大な量の制御機構が必要になるわけですから、量子ビット数が数百万というレベルでは、必要とされる制御機構の設計は現実的には大変難しいのです。通常のコンピュータではバスという概念で同様の問題を解決していますが、現時点では量子コンピュータの実装において量子バスとでも呼べるものは、いまだ大規模には実現していません。
量子コンピュータ実現に対する課題を解決する手段としての量子的間接制御
前述の2つの問題を解決するために、従来からさまざまな研究がされているところですが、新たな側面からの解決手段を探求することも重要です。量子的間接制御という考え方は、まさにその新たな解決手段になり得るものです。
量子的間接制御についてまず説明します。量子的間接制御とは、制御対象となる量子系が、直接操作が可能な量子系(S系)と、間接的にしか操作できない量子系(E系)とからなっていて、S系をうまく操作することで、S系とE系からなる全体を間接制御するという考え方です。例えば、操作が容易で1量子ビットと見なせる量子系、つまりS系として用い得る系として、超伝導体をリング状に配置することで実現できる超伝導量子ビット(図1(a))があります。また直接操作が困難な1量子ビットと見なせる量子系、つまりE系として用い得る系として、ダイヤモンド中の窒素による格子欠陥によって実現されるNV(Nitrogen Vacancy)センタ(図1(b))があります。超伝導量子ビットの上にNVセンタの含まれるダイヤモンドプレートを置くだけで、その2つの量子系は相互作用によってつながり、超伝導量子ビットをS系・NVセンタをE系とする量子的間接制御を行う系が実現します。実際に1量子ビットの量子メモリ(1)をこの系によって実装する実験はすでに行われています。
こういった量子的間接制御の構造が一般的に、前述した第一の問題点であるノイズの増大を効果的に解決できる手段であることは、次のようなかたちで理解することができます。量子系の操作をするには物理的な操作用の配線を配置する必要があります。しかし、物理的な配線がつながっていれば、それが必然的にノイズの侵入する経路にもなります (図2)。他方、ノイズの侵入を減少させようと思うと、操作用配線を減らして、操作性を犠牲にせざるを得ません。つまり、量子系への操作性の高さとノイズ侵入の困難性との間にはトレードオフの関係が存在します。現状の量子コンピュータの実現形態においては、量子系全体への高い操作性を前提としており、そのことがノイズ侵入経路を減らすうえでの限界を与えています。そのため、量子的間接制御のように操作性が低くても、自由に全体制御が可能であることが分かれば、ノイズ侵入経路を減らし、ひいてはノイズ低減自体を高いレベルで実現したうえで、量子情報処理を実現できることが期待されます。
さらに量子的間接制御で量子系全体を自在に制御できることは、前述した第二の問題点に対しても有効に対処可能であることをも意味します。というのも、量子的間接制御はE系にある量子情報をS系に取り出して処理してはE系に戻すことの繰り返しであるととらえることができ、抽象的には量子バスの構造を持っているといえるためです。つまり大規模な量子的間接制御を行えるようになることで実現する機能は、大規模な量子バスを実現することで得られる機能を含んでいます。
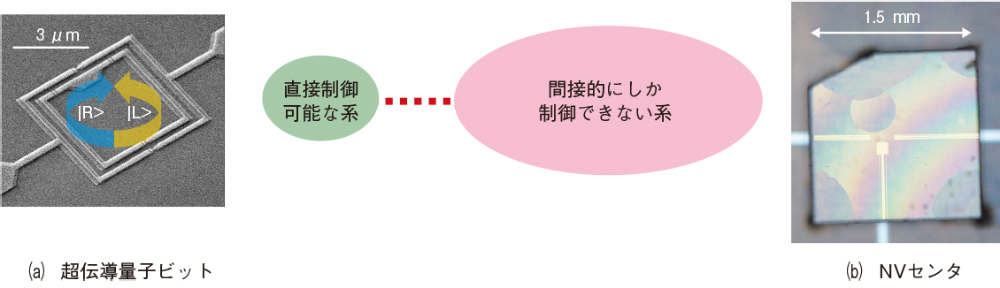
図1 量子的間接制御の例
量子コンピュータを量子的間接制御で実装するにあたっての課題
前述のように、量子的間接制御は大規模な量子コンピュータをつくるうえでの主要な2つの問題を解決する手段となり得ます。にもかかわらず、量子メモリのような小規模な利用例はあるものの、大規模な量子情報処理への実装手段としては検討されず、十分な研究もなされてきていませんでした。というのも、S系とE系をつなぐ相互作用のわずかな違いで、実行可能な制御の種類さえ大きく変わってしまい、そのような状況では情報処理の能力を議論することさえも困難だからです。実際、量子コンピュータとして機能するためには、どんな制御でも実行可能である必要がありますが、与えられた量子的間接制御がそのような性質を持っているかという基本的な質問にさえ、今までは明確に答えることはできていませんでした。
本稿で示す研究成果(2)は、この基本的な質問に対して答えるものです。ある量子系が与えられたとき、その量子系でどのような制御が実行できるかは、動的Lie代数*1と呼ばれる歪エルミート行列*2の集合によって判断できることが知られています。そのため、量子系が与えられたときに、その動的Lie代数が何かを知ることこそが、その量子系が実行できる制御の範囲を調べることに相当します。例えば、現在考えられている典型的な量子コンピュータの場合、対応する動的Lie代数にはすべての歪エルミート行列が含まれることがすでに知られており、そのことは当該量子系においてどんな制御でも実行可能であることを意味しています。
ところが、一般の量子系の場合、一般的に実現し得る動的Lie代数には多くの可能性が存在します。それ故に、量子的間接制御において、上記の基本的な質問にさえ答えを与えることが困難でした。しかし、最近行われた研究(2)によって、操作が量子的間接制御によって行われるという事実さえ仮定すれば、その動的Lie代数にはJordan代数*3と深く関連する構造の存在が要求されることを発見しました。Jordan代数は動的Lie代数に比べて多様性が非常に小さいことが知られています。この事実を使うことで、量子的間接制御の場合の実現し得る動的Lie代数を完全に分類するとともに、量子的間接制御が量子情報処理を実装する手段として有用な性質を持つことが分かりました。
得られた動的Lie代数の分類によると、直接操作可能な量子系(S系)の次元*4によって、動的Lie代数の構造が全く異なることが分かりました。特に、S系の次元が3以上の場合は、量子的間接制御によって、影響を及ぼせる空間に対する任意の歪エルミート行列が動的Lie代数に必ず含まれることが分かりました。つまり、S系の次元が3以上の場合には、実質的に背後にある量子系に対してどのような制御でも実行可能であると認識して良いことを意味しています。つまり、量子情報処理を実装する装置として十分な性能を量子的間接制御は普遍的に有することを意味しています。
脚注:
*1 動的Lie代数:交換子積に関して閉じていて線形空間を成す元からなる集合。つまり、この集合は、この集合の任意の2つの元をA、Bとし、任意の実数をx、yとすると、AB-BA やxA+yBもこの集合に含まれます。
*2 歪エルミート行列:複素共役+転置によって自身に負符号をつけたものになる行列。
*3 Jordan代数:反交換子積に対して閉じていて線形空間を成す元の集合。つまり、この集合は、この集合の任意の2つの元をA、Bとし、任意の実数をx、yとすると、AB+BA やxA+yBもこの集合に含まれます。
*4 次元:通常の情報処理で言うところの基数。例えば3量子ビットからなる量子系は8次元です。
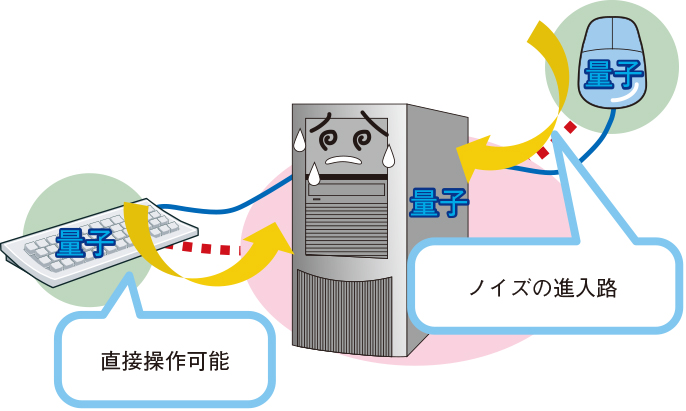
図2 ノイズの侵入経路
まとめ
このように、量子的間接制御の数学的な性質を研究することで、量子的間接制御が量子情報処理を実現する手段として有効であることが分かりました。ここで示した結果をもって、ノイズを非常に低く抑えた量子コンピュータが明日にでも実現するというわけではありませんが、量子コンピュータ実現への課題の解決手段として今まで検討されてこなかった量子的間接制御という手法に可能性が有ることを理論的に示したことは、それ自体が大きな一歩です。さらには、この研究で得られた理論体系を、制御の実行時間をも扱える理論へと発展させることなどで、量子コンピュータ実現へのさらなる大きな貢献ができるでしょう。
■参考文献
(1) X.Zhu, S.Saito, A.Kemp, K.Kakuyanagi, S.Karimoto, H.Nakano, W.J. Munro, Y.Tokura, M.S. Everitt, K.Nemoto, M.Kasu, N.Mizuochi, and K.Semba :“Coherent coupling of a superconducting flux qubit to an electron spin ensemble in diamond,”Nature,Vol.478, pp.221-224,2011.
(2) G.Kato, M.Owari, and K.Maruyama:“Algebra and Hilbert space structures induced by quantum probes,”Ann. Phys., Vol.412, 168046,2020.

加藤 豪
問い合わせ先
NTTコミュニケーション科学基礎研究所
メディア情報研究部
TEL 0774-93-5020
FAX 0774-93-5026
E-mail cs-liaison-ml@hco.ntt.co.jp




量子情報は、実用化がもうすぐそこのものから、まだ夢物語のものまでいろいろなものがありますが、より多くのものを実現していけるよう、理論的な探求を行っていきます。