近年、量子コンピュータの卓越した潜在能力への期待が高まり、世界中で、国家プロジェクトや大小さまざまな企業が熾烈な量子コンピュータ開発競争を演じています。しかし、近い将来実現が期待されるのは、フルスペックの量子コンピュータに比べて機能や規模において制約のある量子コンピュータであると考えられています。その理由は、誤り耐性のある大規模量子コンピュータの実現には、非常に厳しい条件を満たす実装技術が要求されるからです。そのような実装技術を1日でも早く実現するための基礎研究が、まさに今、世界中で進められています。
一方で、理論的知見により、物理実装上の制約からくる量子コンピュータの能力の限界を明らかにする研究も進んでいます。本稿では、計算理論や情報理論の知見に基づいて、機能や規模において制約のある量子コンピュータの能力を最大限利用するための研究を紹介します。

現在想定されている量子コンピュータでは、量子ビットの集まりを用意し、1量子ビットまたは2量子ビットへの操作をあらかじめ決められた順に行い、得られた状態を観測することで出力ビット列を得ます（図1）。量子アルゴリズムとは、出力が問題を解決する情報となるように、量子ビットへの操作を解決したい問題に依存して、うまく設計することです。このとき、扱う量子ビットがノイズの影響を受けないことが重要であることはよく知られています。ノイズの影響を排除するために、大規模な量子コンピュータにおいては量子誤り訂正符号を使うことが検討されています。これは、複数の量子ビット（物理量子ビット）を用いて冗長性を持たせることにより、ノイズの影響を受けない1つの量子ビット（論理量子ビット）を実効的に構成するという手段です。このような手段を実現するために物理量子ビットへのノイズレベルを一定水準以下にすることが求められていますが、現在でもその要求を完全には満たせていません。
そもそも、量子コンピュータにおいてある部分が直接操作できるということは、その部分は外部の状態に応じて影響を受ける（ノイズが侵入する）ことを意味しています。つまり、多様な操作手段を持っていることは、ノイズの侵入経路も多様であることをも意味します。そのため、操作可能な自由度が限られている（量子情報を取り扱うことができる）ものには、ノイズの影響も小さくなります。ところが、現在想定されている量子コンピュータは、通常のコンピュータのアナロジーをその起源としているため、多様な操作を実行できることを前提としており、制限された状況での実用的な情報処理は考察されてきませんでした。
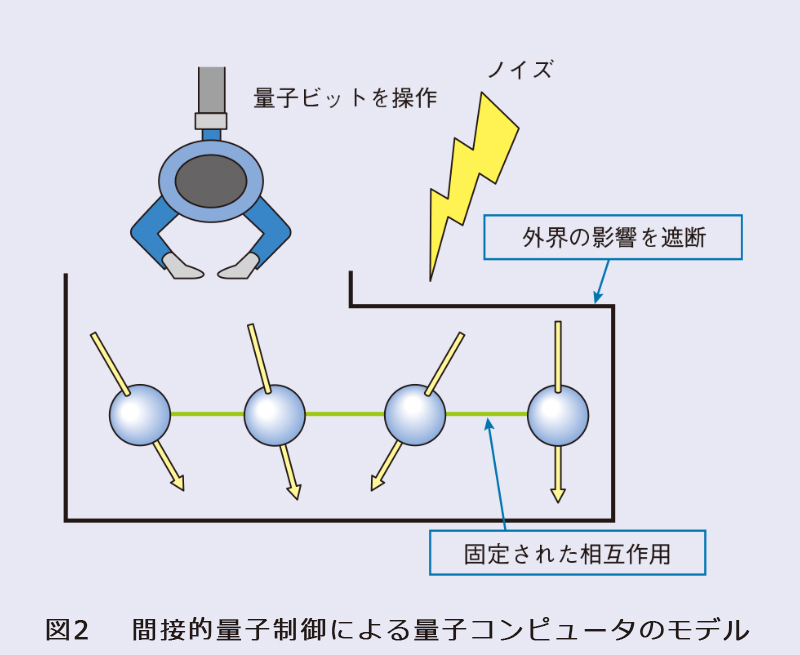
そこで私たちは、量子誤り訂正符号以外でノイズ除去をする方法として、操作可能な手段を制限するという方法を理論的に検討しました（1）。具体的には、内部自由度は大きいものの、外部から直接操作できる自由度は小さなもので、両者の間を何らかの固定された相互作用によって量子情報が行き来するという状況（間接的量子制御）を考え、そのようなものを量子情報の処理を実行する手段として利用できるか検討しました（図2）。その結果、内部自由度は、量子コンピュータとしての観測結果に影響を与えるものと与えないものに綺麗に二分することができることが分かりました。さらに、直接操作できる部分が2量子ビット以上の自由度を持ってさえいれば、結果に影響を与える内部自由度を担う部分に対して、間接的にではあるものの、任意の量子的制御が実行可能であることが分かりました。つまり、多くの部分を直接には操作できなかったとしても、少なくとも2量子ビットの操作が自由にできるのであれば、間接的量子制御は量子情報を処理する物理系として十分な能力を持っていることになります。ただ、この結果は、間接的な量子制御の実現に関する可・不可の議論にとどまっており、所望の量子制御をどの程度の時間で実行できるかなどのより踏み込んだ問いに対する回答を与えることはできていません。この成果は間接的量子制御を考えるうえでの理論的な土台をつくったことに相当するものであり、より実用的な問いに対する回答にはさらなる研究が必要です。

量子コンピュータは、高度に制御された量子系＊1に対して適切な順序で測定を行い、情報を読み出し、そこで得た情報を基に再び量子系の制御や測定を行うという流れに沿って行われます。この中でも、量子系に対する測定は、仮に理想的に行えたとしても量子系に変化を与えてしまうため、測定順序は実装したい量子アルゴリズムから強い制約を受けます。このため、測定順序の自由度を高くできれば、さまざまな量子アルゴリズムが実現できるようになり、量子コンピュータの可能性を広げることに結びつきますし、さらには、安全性の高い秘匿通信（量子鍵配送）の高効率化にもつながります。
一方で、測定までの時間が長くなると、量子系に対する外部雑音を長時間抑える機構（量子メモリ）が必要になります。量子メモリはさまざまなデバイスで研究が進められていますが、依然メモリが有効に働く時間内に行える測定の回数は限られていて、大規模な量子コンピュータを実現するうえでの障壁となっています。これに対し、一見順序どおりに行う必要があるように思える測定（遅延測定）の中にも、量子系へ与える変化をうまく抑えた測定をあらかじめ行うことで測定順序を前倒しできる、すなわち量子メモリなしで実装できるものがあることが知られており、近年その理論的解析が進められてきました。しかし、そのような遅延測定がどのような量子情報処理に応用できるかは分かっていませんでした。
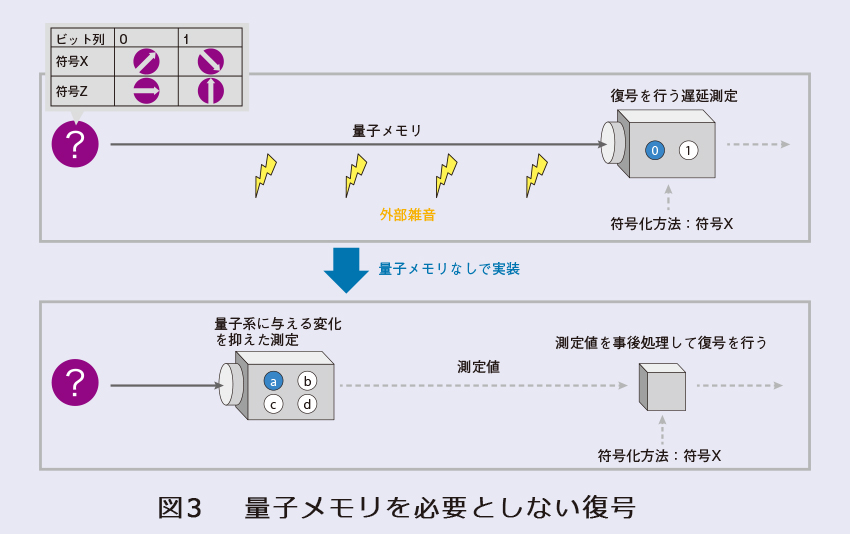
今回私たちは、そのような遅延測定が、量子符号化と呼ばれる、多くの量子情報処理に登場するサブルーチンに応用できることを発見しました（2）。2種類の方法で量子系に符号化されたビット列を、測定により復号することを考えます。このとき、直感的には、符号化方法を知ったうえでそれに応じた遅延測定を行わなければ復号に失敗してしまうように思えます。しかし、私たちは、符号化方法を知る前に測定を行ったとしても、簡単な事後処理を施すことでビット列を誤りなく復号できることを発見しました（図3）。また、そのような符号化方法の完全な特徴付けにも成功しました。さらに、本方法は量子鍵配送に直接応用可能で、通信雑音が無視できる場合には、既存のものよりも高効率な鍵配送が可能であることが分かりました。ただし、実際の長距離鍵配送では通信雑音が無視できないため、通信雑音が存在する下での詳細な効率解析が今後求められます。

＊1 量子系：光子や電子など、量子力学的性質が顕著になる物理系。

量子コンピュータによる高速計算の実現には、高速なアルゴリズムが不可欠です。このようなアルゴリズムは一般に、状態が0に初期化された多数の量子ビットが利用できるという仮定の下で設計されます。多数の初期化済み量子ビットは、アルゴリズムの実行中に生じるさまざまな途中結果の記憶を可能とし、記憶された途中結果は計算の並列化に利用される等、アルゴリズムの高速性能の向上に大きく貢献します。
多数の初期化済み量子ビットは高速なアルゴリズムの設計において大きな役割を果たす一方で、その実現は現在の実装技術では困難であることが知られています。実際、量子ビットの初期化精度には限界があり、多数の量子ビットを初期化しても、一部の量子ビットが意図しない状態となることがあります。したがって、利用できる初期化量子ビットの個数を厳しく制限すると実現性は向上しますが、このような状況の下では高速なアルゴリズムの設計が困難です。
利用できる初期化済み量子ビットの個数をできるだけ制限しつつ、高速なアルゴリズムの設計を可能とするため、私たちは未初期化量子ビットに着目しました。未初期化量子ビットの量子状態は不明ですが、通常の量子ビットと同様に、量子演算を適用して状態を遷移させることができます。初期化を必要としないため、多数の未初期化量子ビットが利用できるという仮定は、実現性を損なうものではありません。
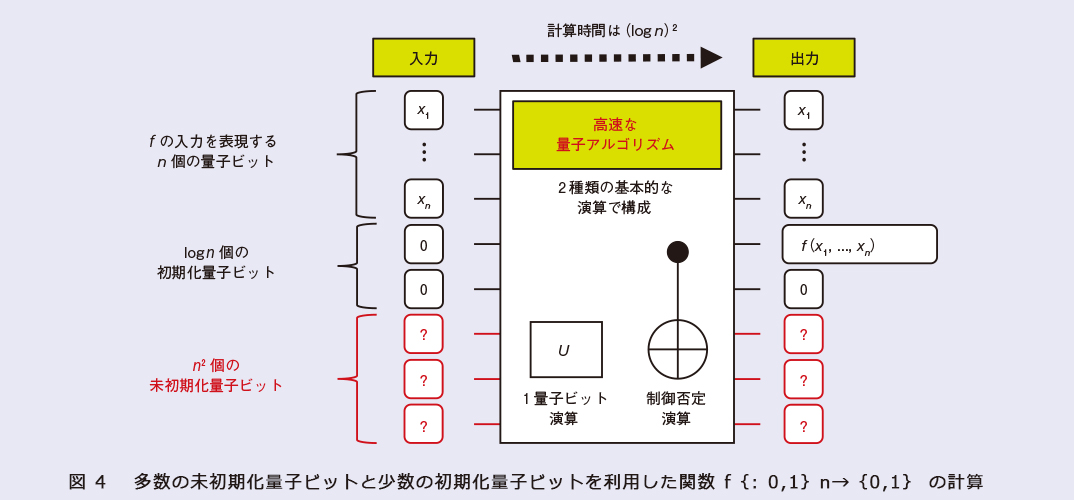
私たちは、多数の未初期化量子ビットと少数の初期化済み量子ビットが利用できるという仮定の下で（図4）、論理和関数等、複雑なアルゴリズムの基礎となる関数を計算する高速なアルゴリズムを設計しました（3）。少数の初期化済み量子ビットだけで同等の高速性能を持つアルゴリズムを設計することは困難であるため、私たちの成果は、未初期化量子ビットが高速なアルゴリズムの設計に大きく貢献することを明らかにしたものとなります。

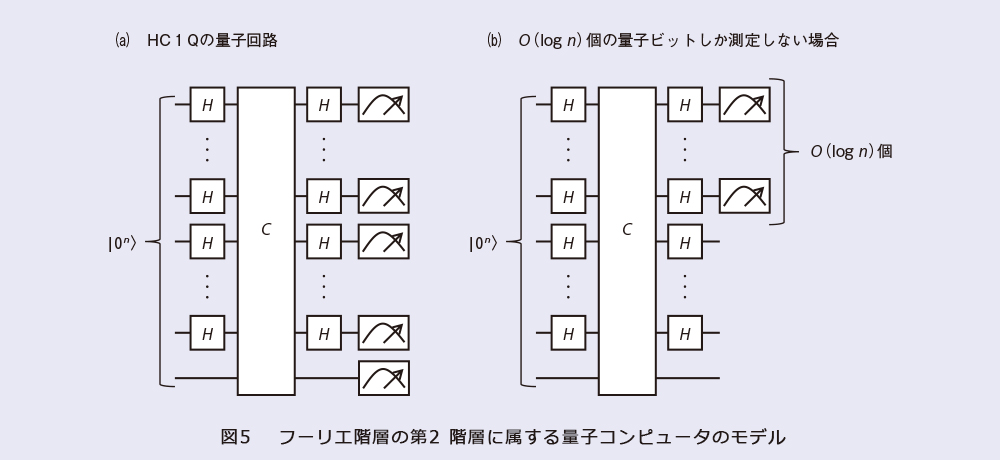
近年、実現性を高めるために機能を制限した量子コンピュータのさまざまなモデルが提案されています。今回、私たちはフーリエ階層という量子回路の階層構造に着目し、図5（a）に示すようなHC1Q（Hadamard-classical circuit with one-qubit）という新しいモデルを提案しました（4）。HC1Qは、重ね合わせで実行する古典計算Cの前後でアダマールゲートH＊2によって基底変換を行うというモデルです。ただし、1番下の量子ビットに関しては基底変換を一度も行いません。フーリエ階層は高次になればなるほど計算能力が高くなっており、1番下の第1階層は古典コンピュータで効率良くシミュレートできてしまうことが分かっています。そのため、古典計算に対する量子計算の優位性（量子超越性）を得るためには少なくとも第2階層以上に着目する必要があります。私たちが提案したHC1Qは第2階層という低次の層に属していながら量子超越性も有しているため、もっとも機能が制限された量子コンピュータのモデルの1つだと考えることができます。私たちは、もしHC1Qを古典コンピュータで効率良くシミュレートできるならば、計算量理論＊3における多項式階層が第2階層まで崩壊するということを示しました。多項式階層とは決定問題（はい、いいえで答えられる問題）の階層構造で、無限個の階層が存在すると強く信じられています。フーリエ階層と多項式階層という全く異なる2つの階層構造を関連付けることで、機能が制限された量子コンピュータのモデルの量子超越性を示したというのが私たちの結果です。図5（a）からも分かるとおり、HC1Qでは入力したすべての量子ビットを測定しています。では、測定する量子ビットの数を減らすとどうなるでしょうか。興味深いことに、測定する量子ビットの数が少ない場合（図5（b））は、古典コンピュータと同等あるいはそれ未満の計算能力になってしまうということが分かりました。

＊2 アダマールゲート：1量子ビットに作用する基本的な量子ゲートの1つ。
＊3 計算量理論：問題の難しさを系統的に研究する学問分野。P≠NP予想は計算量理論の最大の未解決問題。

量子コンピュータ上での高速計算は、ハードウェアとソフトウェアの両輪があって初めて実現することができます。今回紹介したように、理論によってハードウェアの限界を引き出したうえで、ソフトウェアとして何ができるのかを追求していきます。

■参考文献
（1）　G. Kato, M. Owari, and K. Maruyama: “Algebra and Hilbert space structures induced by quantum probes,” Annals of Physics, Vol. 412, p. 168046, 2020.
（2）　S. Akibue and G. Kato: “Perfect discrimination of nonorthogonal quantum states with posterior classical partial information,” Physical Review A, Vol. 99, p. 020102, 2019.
（3）　Y. Takahashi and S. Tani: “Power of uninitialized qubits in shallow quantum circuits,” Theoretical Computer Science, Vol. 851, pp. 129-153, 2021.
（4）　T. Morimae, Y. Takeuchi, and H. Nishimura: “Merlin-Arthur with efficient quantum Merlin and quantum supremacy for the second level of the Fourier hierarchy,” Quantum, Vol. 2, p. 106, 2018.