オールフォトニクス・ネットワーク（APN）の情報処理基盤では、通信ネットワーク・通信基盤から端末デバイスに至るまで光技術を導入することにより、低消費電力、高品質・大容量および低遅延の情報処理の実現をめざしています。従来のネットワーク機器でのデータ処理および端末デバイスでの演算は電子回路で行われていますが、APN情報処理基盤ではそれらに光技術を用いることにより、処理や演算の性能を向上させることを想定しています。光技術の1つに、光論理ゲートで構成され、論理演算等が可能な光回路があります。光回路は、例えば、深層学習の分野における学習アルゴリズムの演算に利用されており、低遅延・低消費電力な演算が可能と示されています（1）。

APN情報処理基盤では、コンピューティングの性能向上のためにさまざまな専用ハードウェアが光回路で実現されます。そのため、APN情報処理基盤の安全性を担保するために必要な暗号専用ハードウェアも光回路で実装し、暗号演算が全体の性能のボトルネックとならないように遅延や消費電力を抑えた回路にすることが望ましいと考えます。そこで私たちは、光信号により暗号・認証の演算が可能な光暗号回路を研究しています。本章では、標準暗号の1つであるAdvanced Encryption Standard（AES）を光回路で実現する方法を紹介します。

AESは、128ビットブロック長のブロック暗号であり、鍵長は128、192、256ビットから選択することができます（2）。ステートと呼ばれる中間値の128ビットを8ビットずつ区切って4×4行列で表現し、暗号化の基本構造であるラウンド関数を繰り返し演算して暗号文を出力します。ラウンド関数は、非線形演算であるSubBytes、線形演算であるShiftRows、MixColumns、およびステートと鍵との加算であるAddRoundKeyから構成されます。本章では、AESの主要な演算であるSubBytesとMixColumnsに着目し、それらを光回路で実現する方法を紹介します。

SubBytesは、8ビットごとに仕様で定められたS-boxテーブルに基づいた変換を行います。S-boxテーブルは、8ビット入出力の非線形変換です。ある8ビットの入力値に対して、テーブルを参照することにより、8ビットの出力値が得られます。例えば、入力値0xf0に対するS-boxの出力は0x8cとなります（入出力の値は16進数で表しています）。
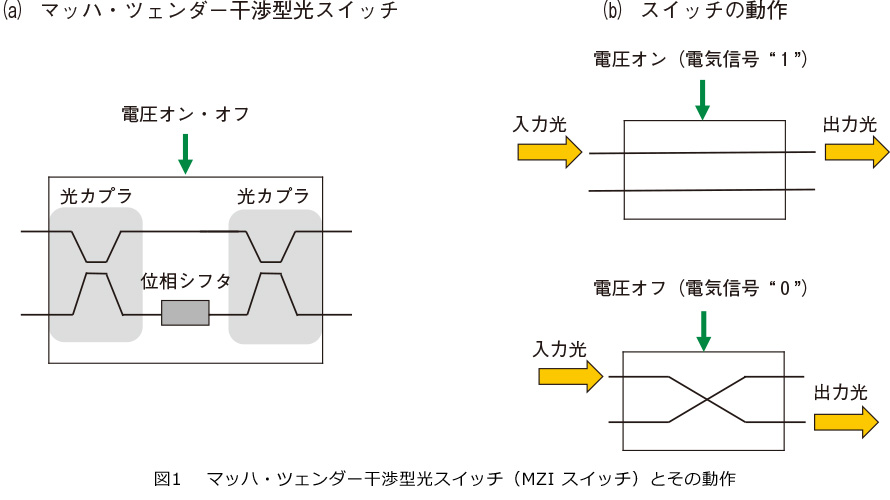
このようなテーブルに基づいた変換は、光論理ゲートの一種であるマッハ・ツェンダー干渉型光スイッチ（MZIスイッチ）を用いて実装することができます。MZIスイッチは、図1（a）に示すように、光カプラと位相シフタから構成され、位相シフタが埋め込まれた経路に電圧を加えるか否かによって光導波路の屈折率の変化を起こすことにより、2つの経路の位相差を変更します。このことにより、MZIは光の経路を切り替えるスイッチとして動作します。例えば図1（b）では、上側の経路に光が入力され、位相シフタが埋め込まれた経路に電圧を加える場合は（電気信号のビット “1”に相当）光信号は直進した経路（上側）から出力され、電圧を加えない場合は（電気信号のビット“0”に相当）光信号はクロスした経路（下側）から出力されます。
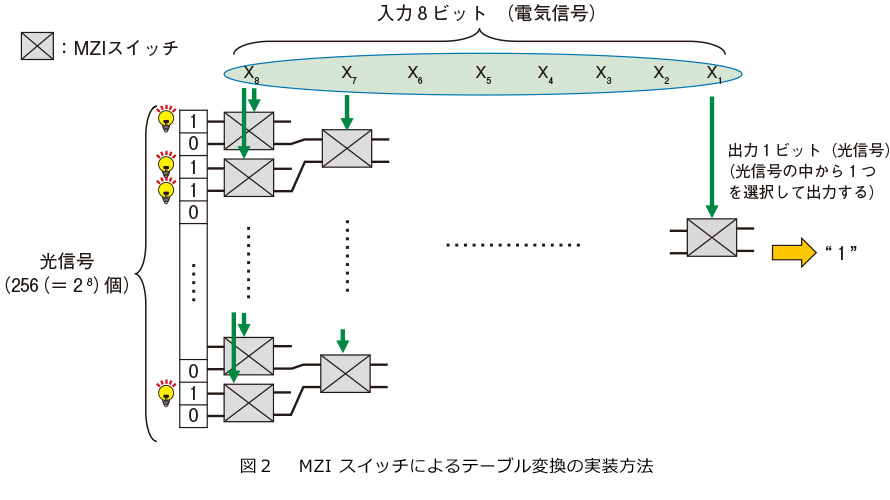
私たちは、テーブル変換の入力ビット数に応じた数のMZIスイッチを接続して経路を切り替えることにより（図2）、入力8ビットに対して1ビットの光信号を出力するテーブル変換の実装方法を考案しました。図2において、単一の光源を分岐した256個（＝28個）の光を用意し、点灯（光信号のビット“1”に相当）または消灯（光信号のビット“0”に相当）と設定します。このとき、8ビットの入力（x₁、x₂、・・・、x₈）に応じて経路を選択しながら光がMZIを通過し、最終的に1つの光信号が選択され、出力されます。このように、MZIを用いて8ビットの入力に対して1ビットの光信号を出力するテーブル変換を実現することが可能です。
前述のように複数のMZIスイッチを接続し、256個の光信号を適切に設定することで、S-boxテーブルを構成することができます。MZIの入力（電気信号）にS-boxテーブルの入力を設定し、光信号にS-boxテーブルの出力を設定します。例えば、S-boxテーブルの各256個の値の最下位ビットを光信号に設定しておけば、入力8ビット（x₁、x₂、・・・、x₈）に対してS-boxテーブルの出力の最下位1ビットを得ることができます。同様に、S-boxテーブルの出力の各々nビット目（n＝1、...、7）を光信号に設定しておけば、8ビットの入力に対するS-boxテーブルの出力のnビット目を得ることができます。
8ビット分のS-boxテーブルの出力を得るためには、上記演算処理を時系列的に8回繰り返す方法や図2の回路を8個並列に実装する方法もありますが、光の場合は波長を8波長に多重化し、波長ごとにS-boxテーブルのnビット目を導出することにより、図2の1つの回路で8ビット分を演算することも可能です。

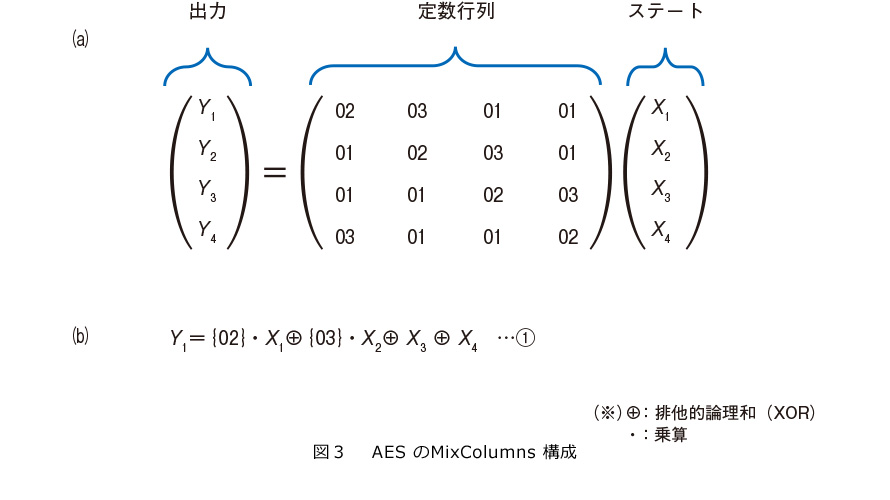
MixColumnsは、図3（a）に示すように、定数行列とステートの乗算で定義されています（X、Yは8ビット）。行列式を計算すると、出力の各8ビットは図3（b）の式①のように表すことができます（図3（b）ではY1のみを示しています）。さらに、乗算を計算すると、式①は5ビットのXOR演算（入力5ビット・出力1ビットのXOR演算）5つと、7ビットのXOR演算（入力7ビット・出力1ビットのXOR演算）3つを用いて表すことができます（2）。ここでは、例として、7ビットのXOR演算を光論理ゲートで構成する方法を紹介します。同様に、5ビットのXOR演算も構成可能です。
XOR演算が可能な光演算素子としてYゲートがあります（3）。Yゲートは、2つの入力信号光が合流する点で信号を重ね合わせます。光信号が振幅と位相を持つ「波」である性質を利用することでXOR演算やOR演算を実現でき、電気による論理ゲートに比べて約300倍の高速な演算が可能です（3）。
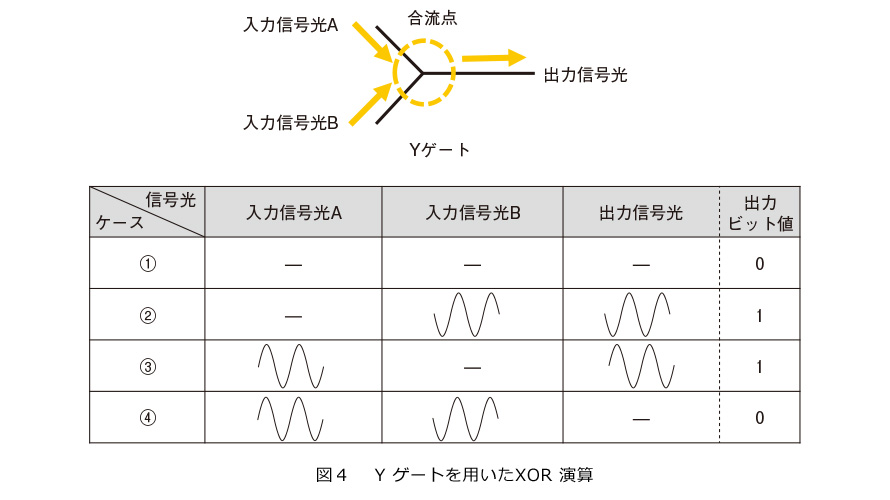
YゲートによるXOR演算の原理を図4に示します。図4のように、位相差が180°で振幅の大きさが同等の2つの信号光（入力信号光Aと入力信号光B）を入力とします。図4の「－」は入力信号光の振幅が0の状態、つまり信号光がない状態を示します。この2つの信号光をYゲートへ入力し、出力光の振幅の大きさを判定します。例えば、図4のケース④の場合、2つの入力信号光の振幅が同等で位相差が180°であるため、信号が打ち消し合い、振幅が0となります。このようにして、振幅が0の状態をビット“0”、振幅の大きさが入力信号光と同程度である状態をビット“1”に対応付けると、図4の出力信号光のビット値に示すようにXORの論理演算を行うことが可能となります。このように2つの入力信号光の位相差を180°にするといった入力光に対する制約をつけることで、Yゲートを用いてXOR演算が可能なことが示されています。
ここで、7ビットのXOR演算を行う際には複数のYゲートをつなげて演算しますが、XOR演算の演算結果を次のXOR演算の入力とする場合は、各Yゲートの2つの入力信号光の位相差は演算結果に依存し、必ずしも180°になるとは限りません〔例えば、4ビットのXOR演算（a⊕b⊕c⊕d）を行う際に、a、bとのXOR演算結果とc、dとのXOR演算結果とが共にケース②の出力となり、その結果をXOR演算する場合など〕。よって、各Yゲートの2入力信号光の位相差を演算結果に応じて変更するといった操作が必要であり、この操作による遅延や消費電力が増加してしまいます。
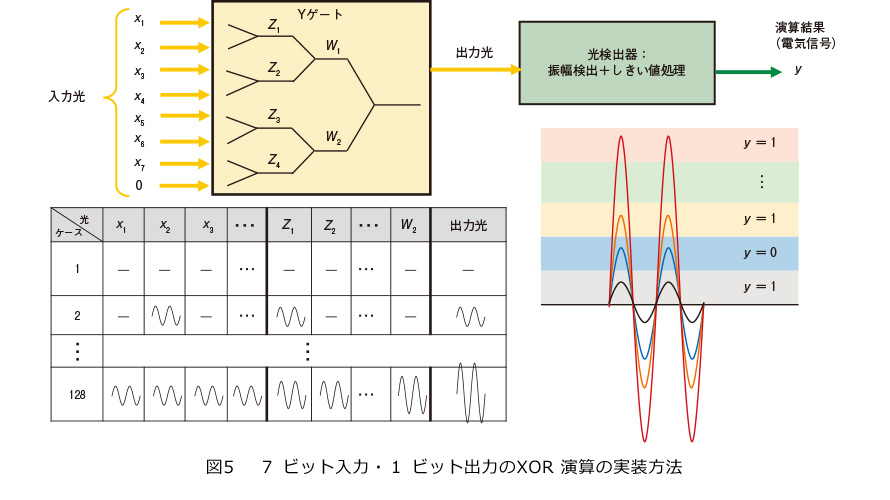
そこで私たちは、演算途中の位相の変換を不要とするために、Yゲートの入力の光信号を同位相として演算し、演算の最後にしきい値処理により出力結果を補正する方法を考案しました。図5にその概要を示します。本手法は、Yゲートの重ね合わせと光検出器内でのしきい値処理により構成されます。Yゲートの重ね合わせでは、合計7つのYゲートを利用して、光の振幅を足し合わせていきます〔入力数が7であるため、8番目は振幅 “0”の光（消灯）とします〕。しきい値処理では、入力光（x₁、x₂、x₃、x₄、x₅、x₆、x₇）の中で光の振幅が0でない信号の数が多いほど、出力光の振幅が大きくなるため、それを検出し、出力のビットを判定します。具体的には、出力光の検出なし（消灯）、または入力光の振幅の偶数倍（2倍、4倍、6倍）の振幅を検出した場合は出力結果をビット“0”、入力光の振幅の奇数倍（1倍、3倍、5倍、7倍）を検出した場合は出力結果をビット“1”と判定します。前述の実装方法により、Yゲートの演算度に入力光の位相を変換する必要なく、XOR演算を行うことが可能になります。本演算方法により、Yゲートの出力の処理を7回（Yゲートの出力の数）から1回（しきい値処理時のみ）に削減することが可能です。
図3（b）の式①から計算される7ビットのXOR演算および5ビットのXOR演算を図5に示す演算方法に対応させると、Y₁の1ビット分を計算することができます。Y₁（8ビット分）を計算するには、SubBytesの演算と同様に、時系列的に演算する、複数の演算回路を用いる、または、1つの演算回路で波長の多重化により演算を行うという実装方法が可能です。

私たちは、光論理ゲートを利用するAES暗号回路の構成方法を考案しました。今後、APN情報処理基盤の安全性を確保するために、さまざまな暗号方式による演算や認証などのセキュリティ技術を光回路で実装する光セキュリティアクセラレータが必要になってきます。このアクセラレータは、図6に示すAPN情報処理基盤を支えるアーキテクチャである光ディスアグリゲーテッドコンピューティング（4）の構成要素の1つになると考えています。従来、CPU・メモリ等の各種デバイスは各サーバ内に閉じていましたが、光ディスアグリゲーテッドコンピューティングは、それらを高速光ネットワークで接続し、分散させることにより、ラック・データセンタスケールのコンピュータとして扱うという新しいアーキテクチャです。光セキュリティアクセラレータは、安全な光ディスアグリゲーテッドコンピューティング基盤およびそれによる安全なスマートサービスの提供につながると考えています。今後も、低遅延・低消費電力の光セキュリティアクセラレータの実現のために、私たちは光の特性を活かした新たな暗号・認証の実装方式の研究を引き続き行っていきます。このことにより、安全なIOWNの実現に貢献していきます。

■参考文献
（1）　J. Peng，Y. Alkabani, S. Sun, V. J. Sorger, and T. El-Ghazawi：“DNNARA：A Deep Neural Network Accelerator using Residue，”ICPP 2020, No. 61, pp. 1-11, Edmonton, Canada, August 2020．
（2）　NIST：“Announcing the ADVANCED ENCRYPTION STANDARD （AES），”Federal Information Processing Standards Publication 197, 2001．
（3）　S. Kita, K. Nozaki, K. Takata, A. Shinya，and M. Notomi：“Ultrashort low-loss Ψ gates for linear optical logic on Si photonics platform,”Communications Physics, Vol. 3, No. 33, pp.1-8, 2020.
（4）　岡田・木原・岡崎：“IOWNを支えるディスアグリゲーテッドコンピューティング,”　NTT技術ジャーナル, Vol. 33, No. 5, pp. 40-44, 2021．