2022年6月号
特集
電流注入結合フォトニック結晶レーザを用いた例外点縮退の観測
- 非エルミートフォトニクス
- 例外点
- フォトニック結晶レーザ
結合共振器や結合導波路に増幅利得や吸収損失の差を導入した系は非エルミート光学系と呼ばれ、実用性が期待される数々の新奇現象を示すことが報告されてきました。私たちは、非エルミートナノフォトニクス技術の確立へ向け、利得および損失の精緻な制御が可能な電流注入フォトニック結晶レーザの結合系を実現しました。本稿では、同素子による、例外点と呼ばれる非エルミート系特有のモード縮退と、それによる特異な発光増強の実証について紹介します。
高田 健太(たかた けんた)†1、2/野崎 謙悟(のざき けんご)†1、2
倉持 栄一(くらもち えいいち)†1、2/松尾 慎治(まつお しんじ)†1、3
武田 浩司(たけだ こうじ)†1、3/藤井 拓郎(ふじい たくろう)†1、3
北 翔太(きた しょうた)†1、2/新家 昭彦(しんや あきひこ)†1、2
納富 雅也(のうとみ まさや)†1、2
NTTナノフォトニクスセンタ†1
NTT物性科学基礎研究所†2
NTT先端集積デバイス研究所†3
非エルミートフォトニクス
光信号を生成し制御するためには、レーザ、変調器、光検出器といった素子が必要です。これらは、光波を誘導放出により増幅したり、信号線から放出したり、あるいは半導体に吸収させたりして、光強度を変化させます。電磁気学におけるマクスウェル方程式では、媒質における増幅利得や吸収損失は、その屈折率の虚部として表されます。有限の屈折率虚部を持つ媒質により構成された共振器や導波路では、存在可能な光波の状態(固有モード)の周波数や伝搬定数(固有値)も一般に複素数になります。そして固有値の虚部は、共振器での光閉じ込め時間ないし、導波路での光伝搬距離に応じた光学利得または損失のレートに対応します。
注目する物理量(この場合は光波)に関してエネルギーが保存する過程に基づく系をエルミート系と呼ぶのに対し、このような、エネルギーの保存しない過程に基づく系のことを、非エルミート系と呼びます。非エルミート光学系のモード固有値は上記のとおり複素数となるため、光波はキャリアの応答が飽和するまで増幅または吸収され続ける、あるいは系から放出され続けるといったことが起こります。加えて、エルミート系とは異なり、非エルミート系では固有モードどうしが一般に直交しません。エネルギー散逸のない、完全に閉じた系の測定はそもそも不可能であることを考えれば、私たちが観測する状態はすべて、程度の差はあれ非エルミート系のものだということになります。しかし、これらは実は完全には独立ではなく、多かれ少なかれ、他の状態と混ざっているというわけです。多くの場合で近似的に用いられるエルミート系の枠組みと比べると、このような非エルミート系の応答は、はるかに多様でとらえづらいもののように思われます。また、従来フォトニクスの分野では、利得や損失は文字どおり光波の強度を制御するためのものという見方が強く、それ以外の用途へ向けた原理現象の模索は限られていました。
■PT対称性
これらの情勢の転機となったのが、セントラルフロリダ大学のChristodoulides教授のグループによる、PT対称性(Parity-Time symmetry)の概念のフォトニクスへの導入(1)です。PT対称性のPは空間反転を意味します。これは、空間内に中心軸ないし対称面(両面鏡)を設定し、それに対して系を反転させる(鏡の中の世界に移る)ことに対応します。Tは時間反転を表し、ここでは利得を損失に、損失を利得に逆転させることを意味します。ある系にこれらの操作を両方行ったときに、元に戻ることをPT対称であるといいます。元々PT対称性は量子力学において注目を集めていた概念ですが、Makrisらは、光学系の屈折率分布において、上記の意味でのPT対称性(のアナロジー)が成立することを示しました。そして、そのような系では、例外点(Exceptional point)と呼ばれる特異なモード縮退が現れることを明らかにしました。
PT対称な光学系の特性を、図1(a)のような結合二共振器系を例にとって説明します。それぞれの共振器は、単独では全く等しい共鳴周波数の固有モードを持つとします。それらが波長オーダの間隔で並べられたとき、一方の共振器モードのうち、わずかな場がエバネッセント波*1により他方に染み出すことで、互いに結合します。2つの共振器が等しいレートの損失γと利得−γを持つとき、系はPT対称となります。
*1 エバネッセント波:フォトニック結晶やミラーなど、ある波長域において伝搬モードがないような媒質で光が反射されるときに、指数的な空間減衰を伴って媒質内に浸入する微弱な光波のことを指します。
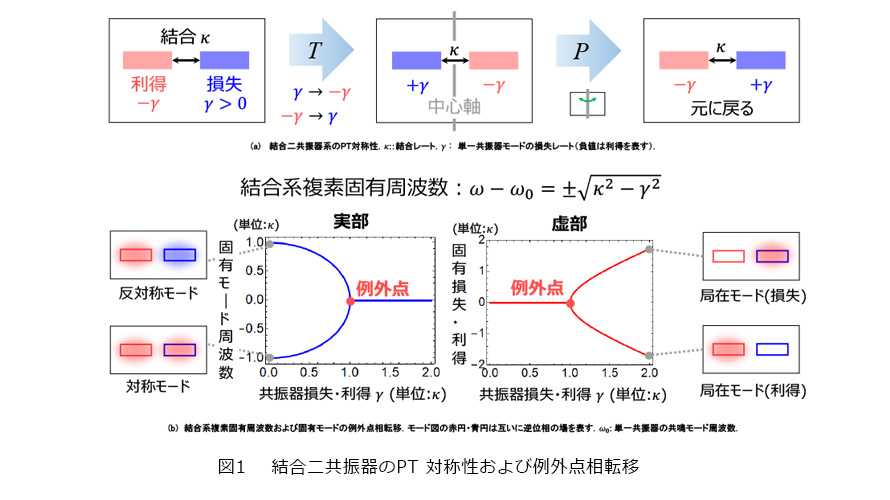
■例外点相転移
共振器間結合レートをκと置き、釣り合った共振器利得・損失レートの絶対値γを変化させたとき、系の応答がどう変わるかを図1(b)に示します。左右のプロットは、それぞれ単一共振器モード周波数ω0を基準にした結合系固有モード周波数(複素固有周波数実部)、およびそれらの正味損失レート(同虚部。負値は利得)を表します。γ=0の場合はエルミート系に対応し、2つの固有モード周波数は結合により2κだけ分裂します。また、固有モード分布は対称モード、反対称モードと呼ばれる2つの直交した状態になります。γを増加させると、周波数分裂は小さくなっていき、γ=κにかけて急速にゼロへと変化します。このとき、二共振器に同じだけの強度の光が分布するため、固有モードの利得・損失は丁度釣合い、そのレートはゼロとなります。γ>κになると、2つの固有モード周波数は等しいままで、今度は固有損失・利得レートが正負の二値へ急峻な分裂を示します。ここでは結合系にもかかわらず、γの増加により固有モードは局在していき、利得を持つ共振器に局在するものは利得、他方は損失を受けます。各共振器の利得・損失と結合のレートが等しくなり(γ=κ)、2つの固有モード周波数が一致する瞬間では、固有損失・利得レートも分岐する直前で、等しくゼロになっています。このとき、2つの異なる状態がたまたま同じ複素周波数を持つのではなく、固有モード分布も全く同じになるため、実は状態は1つになっています。この意味での縮退が、例外点と呼ばれる非エルミート系特有の現象です。例外点は、系全体に広がったモードから、一方の種類の共振器に局在したモードへの相転移点であるともいえます。
これまでに、主に例外点の周りの上記の状態変化に基づく、数々の新奇現象が報告されています。詳細については参考文献(2)に譲りますが、非相反伝搬*2や単一モード発振、周波数摂動効果の増強など、応用への展開が期待されるものも多いため、近年注目を集めています。例えば非相反伝搬は、反射などによる戻り光からレーザを保護する光アイソレータの実現に必要な条件です。光アイソレータの集積は技術的に困難とされていますが、チップ内で完結した光情報処理を行ううえで重要な要素です。例外点近傍の非相反特性は利得飽和に基づき、入力光強度依存性を有するため実用化には壁がありますが、研究の進展が期待されています。
*2 非相反伝搬:磁気光学効果、非線形光学効果、または時間変調効果により、光回路の入出力関係を表す散乱行列が非対称になる条件下での伝搬を指します。
結合フォトニック結晶レーザによる例外点縮退の観測
一方で、いくつかの技術的課題から、フォトニクスにおける例外点縮退そのものの観測例は非常に少ないのが実情です。その1つは、利得や損失の精緻な制御が必要になる点です。例外点は、文字どおり利得・損失パラメータ空間における一点であり、その周りでは複素固有周波数が大きく変化します。そのため、例外点縮退を観測するには、個々の共振器の利得・損失を独立かつ連続的に制御する必要があります。もう1つは、利得・損失の制御に伴う個々の共振器周波数の変化です。前述の制御性を備えた結合共振器の候補としては、複数のオンチップ半導体レーザの集積系が第一に考えられます。しかし、これらの駆動には熱や自由キャリアの発生が伴うため、利得・損失差の導入時に各共振器媒質の屈折率実部も変化し、個々の共振器モード周波数がずれてしまいます。この周波数離調により例外点は消失しまうことが知られているため、可能な限り励起効率の高いレーザを用い、この影響を小さく抑える必要があります。
■電流注入結合フォトニック結晶レーザ
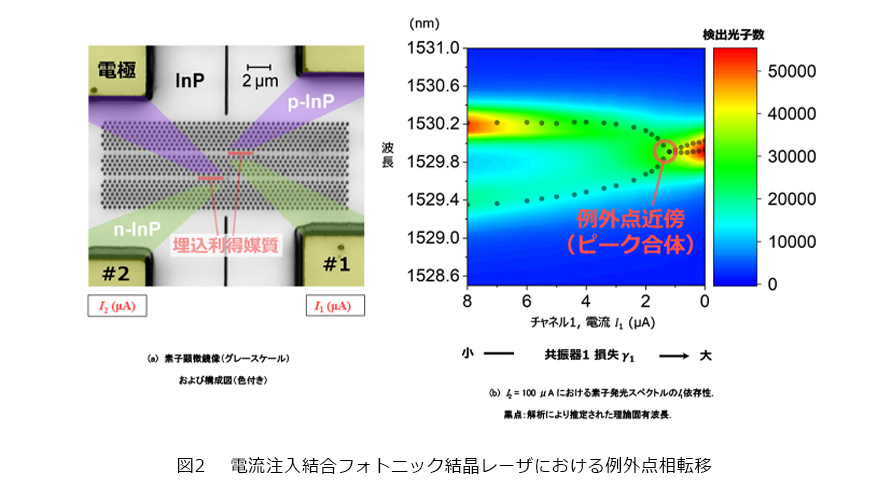
そこで私たちは、図2(a)のような電流注入フォトニック結晶レーザの結合系を作製しました(3)。この系は、中空に保持されたインジウムリン薄膜に直径200nm程度の空気穴の配列を開けた二次元フォトニック結晶と、穴のない線欠陥部分に埋め込まれた、量子井戸を含む波長スケールの利得媒質*3からなるナノ共振器2つ(図中赤色に着色)を持ちます。また、図のように四隅の電極部分(黄色)から埋込媒質へ、斜め方向にpドープ層(紫色)およびnドープ層(緑色)が形成されており、これらが面内の電流注入チャネルを構成しています。この構造により、チャネル間の漏れ電流が抑制されるため、各共振器の利得・損失の独立制御が可能です。さらに、このような埋込媒質型フォトニック結晶レーザは、世界最小の発振しきい値電流を実現しているデバイス技術です(4)。そのため、系の低電流駆動により、熱やキャリアによる共振器周波数離調の影響を最小限に抑えられます。
図2(a)の右、左の共振器および電流チャネルの番号を1、2、各チャネルの電極間電流値をそれぞれI1、I2とし、I1、I2を制御しながら系の発光スペクトルを調べました。その結果、I2=100µAに固定し、I1を減少させていくと、明瞭な例外点相転移を観測できることが分かりました。図2(b)に、このときの各I1に対する発光スペクトルの遷移をカラープロットにしたものを示します。ここでのI2の値は、共振器2が元々持つ吸収や放射による損失γ2が、電流注入により補償される条件です(γ2〜0)。対して、共振器1では有限の損失γ1が残っているため、系全体はレーザ発振せず、微弱な自然放出光が観測されます。I1が小さくなるにつれ、2つの結合モード発光ピークが互いに近づき、合体するのが見られます。これは、I1の減少によりγ1が増加し、二共振器の損失の差が大きくなることで、図1(b)と同様の固有モード周波数変化が起こるためです。ここで、理論モデルを用いたスペクトルのフィッティングにより、各共振器モードの周波数や共振器間結合κ、および損失γ1を見積ることができます。その結果、I1=1.4µA近傍の条件が非常に例外点に近く、またこのとき、弊害となる二共振器の周波数離調も非常に小さくなっていることが分かりました。これは、フィッティング結果から算出した理論固有波長(図2(b)黒点)が、当該の領域で一点に合わさることからも見て取れます。I1をさらに小さくすると、損失が大きくなるにもかかわらず、ピーク光子数が増大することが分かります。これは、固有モードのうちの1つが注入電流の大きい共振器2に局在化することで、共振器1の損失の影響を受けにくくなるためであると考えられます。このことも、図1(b)で説明した例外点相転移を強く示唆しています。
*3 利得媒質:短波長光の照射や電流注入の下で電気キャリアの反転分布を形成し、それに基づく誘導放出により、自然放出波長域の光を増幅できる媒質を指します。本実験では、電流注入のない、または小さい利得媒質が、光吸収体として働くことを用いています。
■例外点における自然放出スペクトル
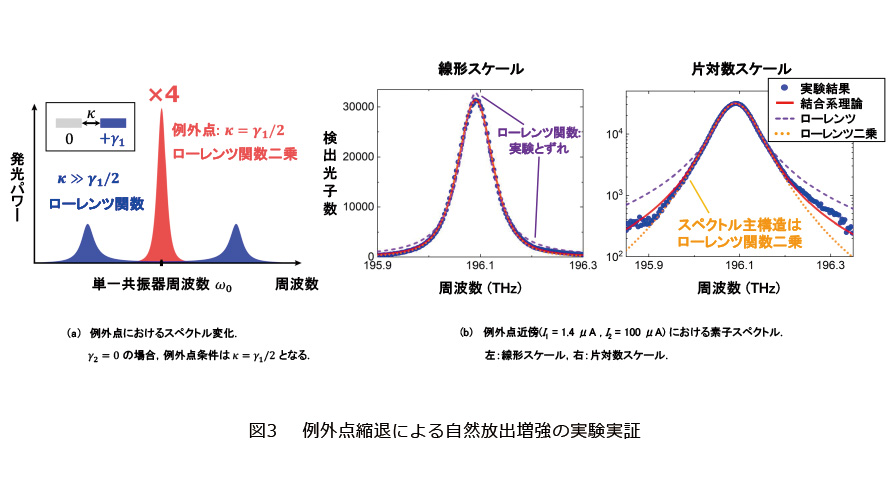
加えて、観測された例外点ごく近傍の発光スペクトルが、特異な発光増強を示唆することも明らかにしました。実験のように、片方の共振器の損失が補償され、もう一方が損失を持つ場合でも、結合が大きい場合の自然放出スペクトルは分裂した2つのローレンツ関数*4として表されます(図3(a)青色)。これに対し、例外点では発光スペクトルがローレンツ関数の「二乗」の形状になります(5)(図3(a)赤色)。系がエルミート系に近似できるようなときには2つのモードはほぼ独立ですので、仮にそれらのピークが偶然重なることがあっても、発光スペクトルはそれらの和、つまりピーク強度が2倍のローレンツ関数にしかなりません。これに対し、例外点では2つのモードが全く同じ状態に縮退しますので、ピークが合体する際に強め合いの干渉を起こします。もし、系のエネルギーを常に保存する結合κのみを変え、それ以外の要素を一定に保ちながら状態を例外点へと変化させることができるならば、純粋な例外点縮退によるスペクトル変化が得られます。この場合、干渉による強度変化が最大限得られ、例外点スペクトルのピーク強度は、分裂した個々のローレンツ関数と比べて(1+1)2=4倍になります。エネルギー保存のため、図3(a)の2つのスペクトルの総積分パワーは同じであり、かつ固有モード損失も等しいのですが、例外点では干渉によりピーク強度が増強した分、スペクトル形状がローレンツ関数二乗型に変化し、線幅がローレンツ関数のピークより細くなるのです。
今回の素子で制御できるのはレーザ間の結合ではなく各レーザの利得・損失です。測定結果には、損失γ1の増加によりピーク強度が減少する効果が重畳していますので、直接観測された例外点縮退によるピーク強度増強の割合は30%程度です。しかし、図3(b)のように、例外点に一番近いI1=1.4µAにおける素子発光スペクトルが、ローレンツ関数の二乗型となっていることも観測できました。この結果は、系がほぼ完全な例外点縮退下にあることを示唆します。またこのことは、発光モードの線幅に対して複素周波数分裂が十分小さい条件まで系が例外点に近づけば、例外点縮退の効果が明瞭に観測できることを意味しています。
*4 ローレンツ関数:指数的なエネルギー減衰を示す、一般の共振器による応答(今の場合、自然放出に基づく発光)のパワースペクトル形状を表す関数の名前です。ノイズの影響が大きい場合、この形状はガウス関数型になってしまいます。本実験におけるスペクトル解析は、デバイスの低ノイズ電流駆動、および長時間積算による低ノイズ測定により成り立っています。
今後の展望
本稿では、電流注入結合フォトニック結晶レーザを用いた例外点縮退の観測について紹介しました。私たちは、結合レーザアレイの例外点を用いた光の群速度制御(6)や、利得・損失による光トポロジーの制御(7)等の理論提案も行っています。より大規模な系を用いたこれらの実証や、さらなる新原理・現象の発見へ向け、日々研究を行っています。
■参考文献
(1) K. G. Makris, R. El-Ganainy,D. N. Christodoulides,and Z. H. Musslimani: “Beam Dynamics in PT Symmetric Optical Lattices,” Phys. Rev. Lett.,Vol. 100,No.10,103904,2008.
(2) Ş. K. Özdemir, S. Rotter, F. Nori, and L. Yang: “Parity–time symmetry and exceptional points in photonics,” Nat. Mater., Vol. 18, No. 8, pp. 783-798, 2019.
(3) K. Takata, K. Nozaki, E. Kuramochi, S. Matsuo, K. Takeda, T. Fujii, S. Kita, A. Shinya, and M. Notomi: “Observing exceptional point degeneracy of radiation with electrically pumped photonic crystal coupled-nanocavity lasers,” Optica, Vol. 8, No. 2, pp. 184-192, 2021.
(4) K. Takeda, T. Sato, A. Shinya, K. Nozaki, W. Kobayashi, H. Taniyama, M. Notomi, K. Hasebe, T. Kakitsuka, and S. Matsuo: “Few-fJ/bit data transmissions using directly modulated lambda-scale embedded active region photonic-crystal lasers,” Nat. Photon., Vol. 7, No. 7, pp. 569-575, 2013.
(5) A. Pick, B. Zhen, O. D. Miller, C. W. Hsu, F. Hernandez, A. W. Rodriguez, M. Soljačić, and S. G. Johnson:“General theory of spontaneous emission near exceptional points,” Opt. Express, Vol. 25, No. 11, pp. 12325-12348, 2017.
(6) K. Takata and M. Notomi: “PT-Symmetric coupled-resonator waveguide based on buried heterostructure nanocavities,” Phys. Rev. Appl.,Vol.7,No.5,054023,2017.
(7) K. Takata and M. Notomi: “Photonic topological insulating phase induced solely by gain and loss,” Phys. Rev. Lett., Vol. 121, No. 21, 213902, 2018.

(上段左から)高田 健太/野崎 謙悟/倉持 栄一
(中段左から)松尾 慎治/武田 浩司/藤井 拓郎
(下段左から)北 翔太/新家 昭彦/納富 雅也






前稿の上梓からおよそ4年が経ちました。本研究はたくさんの方々の協力の下で行われましたが、それでも、測定系の構築や装置の購入に始まり、実験、解析、論文執筆とその出版に至るまで、長い時間を要したことを実感しています。