数学研究の目的は、未解決問題の解決と新しい問題を発掘して数学を豊かにすることです。それにより、すぐにはみえない応用も生まれます。本稿では“対称性に視点をおく量子相互作用と数論の研究”を例に、筆者の研究動機、目的と成果、それらを踏まえた今後の目標について解説します。なお本稿で扱う相互作用は、非可換調和振動子（NCHO: Non Commutative Har­mon­ic Oscillator）^（1）、量子ラビ模型（QRM: Quantum Rabi Mod­el）と非対称量子ラビ模型（AQRM: Asymmetric QRM）です。
数学研究の特質の1つは、離れてみえていた事実を統一的に理解しようとする営みです。長い間、互いに無縁だと信じられてきたものの間に、疑いようのない親近性が明確にされていくことには特別の価値があります。ポアンカレによると、数学は同一視の技術です。朝永振一郎も“うまくいったのは、実験と実証と数学による抽象化である。抽象化によって非常に普遍化できる。これらは物理学の非常な強みだ”としています。他方、数学の定理は発明ではなく発見するものです。これは、存在しているが隠れた数学的真実を、紙と鉛筆で掘り出すのが数学研究だとする小平邦彦＊1の考えにおいても明確です。
さて、タイトルにある対称性とは、群の作用を考えるというものです。群や群の作用といえば、ユークリッド平面・空間の合同変換群や物理や化学などで馴染みの結晶群を思い起こされる方も多いと思います。群論は、20歳のときに決闘で亡くなったガロアにより創始されました。ガロア以前は、2次方程式の根の公式、さらに3次、4次方程式の公式と続き、5次以上の方程式のそれを求めることへの努力が続いていました。しかし、ガロアが行ったのは、方程式の根の置換の全体（置換群）を考え、その構造から、方程式が5次以上の場合、一般には（四則演算とべき根をとる有限回の操作で根を表示する）根の公式は存在しないというものでした＊2。これは大きなパラダイムシフトです。ところで、構造とは何か、ということですが、それは群の非可換度の強さが関連します。シャツを着てからスーツを羽織るのと、スーツを着てからシャツを着るのとでは大違いです。このようなことから、非可換な操作（作用）のイメージを掴んでいただければと思います。

＊1　小平邦彦は日本で最初のフィールズ賞受賞者です。代数曲面として重要なK3曲面はヴェイユが代数幾何学者（クンマー、ケーラー、小平）と当時未踏峰だったK2に因み名付けたものです。夏目漱石の短編集『夢十夜』の第六夜に、運慶が護国寺の山門で仁王像を彫る描写があります。見ていた一人が、運慶の様子をとらえ、“彫っているのではなく、もともと木の中に埋まっている仁王を掘り出しているだけだ”というわけです。これは小平が説明に使っていたものです。数学は、科学に必須の再現性を、厳密証明という手立てで担保していますが、自然が相手というよりは、数学的自然の解明に向かう科学です。

＊2　ガロア理論の始まりです。ガロア理論に接したことで数学者をめざした数学者も多くいます。なお、現在では2次方程式の「解の公式」と呼びますが、かつては「根の公式」と呼びました。2次方程式もいろいろな方程式の1つですので、解であることには違いありません。しかし、負の数の発見や虚数の発見をみても、それは人類の数学世界をひろげるルーツでもありました。特別な思いを込めてroot（根っこ）としておきたいと思います。また、5次方程式の根の公式の非存在自体は、ガロアと同時期にアーベルとルフィニによっても示されていました。ただしそれは、少なくとも表面的には、ガロアのような「群」という意識はみえない技術的なものでした。

量子調和振動子は光子や水素原子の振る舞いを扱う量子論において基本です。そのエネルギー（固有値）は半整数で与えられ、対応する固有状態はエルミート関数です。このことはトレース０の2次の実行列からなる2次元リー環sl₂(R)の表現論＊3から綺麗な記述が得られます。リー環sl₂(R)は、行列式が１の実行列全体がなすリー群SL₂(R)の無限小作用をとらえます。ここで一般に、リー群論は代数方程式のガロア理論に感動したS.Lieが、微分方程式に対するガロア理論を構築しようと創始しました。リー群は、その名の如く群であり、かつ、多様体と呼ばれる幾何的図形でもあります。したがって、sl₂(R)はSL₂(R)の単位元での接空間です。
エルミート関数は実数上の2乗可積分関数がなすベクトル空間 L²(R)の基底をなします。エルミート関数のような特殊関数の多くはガウスの超幾何関数 F（a,b,c;x）のパラメータa,b,cのいずれかを整数値などに特殊化することで得られます。F（a,b,c;x）は3点（0,1,∞とできる）の確定特異点を持つ2階線形常微分方程式の解として定義されます。19世紀以来数学の華であり続ける楕円曲線の整数論にガウスの超幾何は欠かせません。一方、表現論に目を転じると、ガウスの超幾何やその多変数版などに由来する特殊関数は、本質的にリー群の表現の行列要素として理解できます。以下に着目点を示します。
①調和振動子の固有値は半整数（標準的な正規化のもと）。よって、固有値から定まる調和振動子のスペクトルゼータ関数＊4はリーマンゼータ関数ζ(s)＊5と本質的に一致。
②SL₂(R)の対称性はガウスの超幾何の世界にとどまる。
①、②の背後にはSL₂(R)があります。広い世界の探究には対称性を弱める必要があります。調和振動子が持つ非可換性は、sl₂(R)で制御される正準交換関係のみです。微分方程式系を定めるNCHOには行列の非可換性が加わります。その定義には2つのパラメータα、βが必要であり、名称はこの非可換性に由来します。もちろん闇雲な定義ではいけません。要請したのは、NCHOのハミルトニアンQが実離散固有値のみを持つこと、また、α=βにおいて調和振動子が復元できる程度には弱い対称性を持たせることです。前者はQが正値エルミート作用素であることを求めます。後者は、Qのスペクトルゼータ関数ζ_Q(s)がζ(s)の良い拡張となることです^（2）。
ζ(s)の定義級数の収束域は半平面のみですが、ζ(s)は全平面に解析接続（一意に拡張）されます。そしてリーマン予想とはζ(s)=0となる虚数の実部がすべて12だとの主張です。ところで20世紀数学の頂点にはリーマン予想の類似物が2つあります。合同ゼータ関数のヴェイユ予想と、素測地線分布に関するセルバーグゼータ関数に対するものです。どちらの予想も、各ゼータ関数がエルミート作用素による行列式表示を持つことで決着がつきました＊6。本来のリーマン予想の攻略でもζ(s)の行列式表示を探求することが重要です。

＊3 表現論は対称性の学問といわれます。代数、幾何、解析の交流点にあり、おおよそ対称性に着目する数学では欠かせないものです。群の表現論であれば、作用する空間（一般には無限次元）に元のそれぞれが線型変換として定まり、群の積が線型写像の合成として保たれるものです。ここではヴェイユ表現という、掛け算作用素12 X²、微分作用素- 12 d²dX²、そしてオイラーの次数作用素 X ddX + 12たちがなすsl₂(R)の表現を使います。
＊4　重複度が一定に抑えられている正の固有値λ₁≦λ₂≦λ₃≦…を持つ作用素のスペクトルゼータ関数とはディリクレ級数λ₁^-5+λ₂^-5+λ₃^-5+…で定義されるものです。
＊5　ζ（s）:＝1+2^-5+3^-5+4^-5+5^-5+…=（1–2^-5）^-1×（1–3^-5）^-1×（1–5^-5）^-1×（1–7^-5）^-1×（1–11^-5）^-1×…（オイラー積）は、複素数sの実部が１より大きいときにのみ収束します。リーマン予想（1859年）の提出以来160年余を経過した現在も未解決です。多くの天才たちの挑戦が続くこの予想は、コッホ曲線で有名なコッホにより示されたように素数の究極的分布と同値です。
＊6　有限体上の代数多様体・スキームに対して定まる合同でゼータ関数の場合はフロべニウス作用素とよばれるものの行列式表示により肯定的に解決され、セルバーグゼータ関数の場合には、複素上半平面の不変微分作用素であるラプラシアンによる行列式表示により解決されました。

I.Rabiは1936年に光と2準位原子の相互作用の様子を記述しました。後1965年に、JaynesとCummingsが光も量子化しQRMを定めました。ところがQRMの可積分性が不明である一方、その回転波近似であるJaynes-Cummings模型には（連続的な）不変量が存在して理論的扱いが容易であり、実験にも合うことから重宝されました＊7。しかし、量子コンピュータの実現も射程におく近年、技術が発達してJaynes-Cummings模型が実験に合わない例が報告されることになりました。そうした中、2011年にはD.Braak^（3）がQRMの可積分性を示して一気に周辺研究が進みました。事実、超伝導人工原子による実験測定結果^（4）は（A）QRMの理論のとおりでした^（5）。
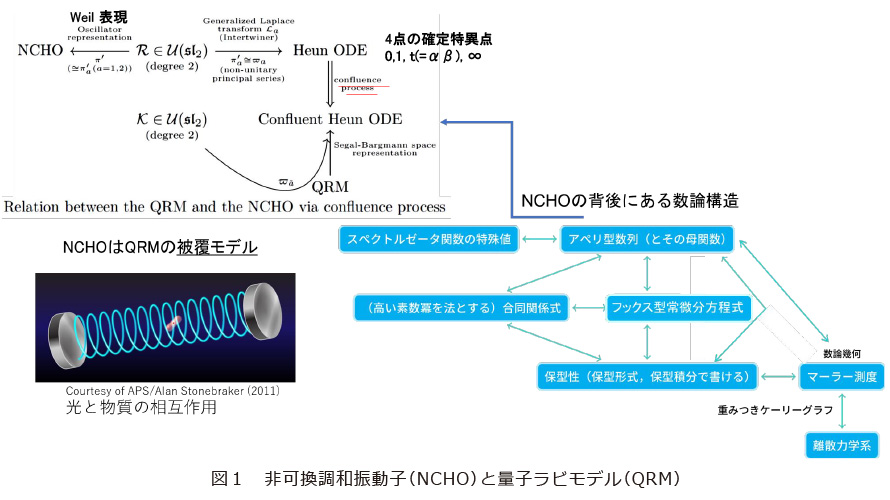
NCHOは期待どおり世界を広げました。実際、NCHOの固有値問題はホイン微分方程式＊8の、0、1を含みαβを含まない領域の正則関数の存在と同値であることが分かりました。この事実は落合啓之が発見^（6）し、その15年後に完全な理解に至りました^（7）。一方で、（A）QRMもホイン描像を持ちます^（3）。ただしNCHOとは異なり合流型の方程式です。ところが、αβ→∞として特異点を合流させるとNCHOのホイン描像からQRMの合流ホイン描像が得られることも分かりました^（7）。NCHOはQRMの被覆モデルだったのです＊9（図1）。
量子化は離散化であり、それは数論の舞台です。実際、（後述するように）NCHOのζ_Q(s）の特殊値には、豊かな数論性がみられます。ゼータ関数の特殊値といえば、古くはオイラーが解決したバーゼルの問題＊10があります。一般にζ（s）の偶数点での値は円周率πの冪と有理数で表されます。しかし、奇数点となると、1978年のR. Apéryによるζ（３）の無理数の証明まで300年以上の間不明のままでした。今なお、無理数性に関する最良の成果は、5、7、9、11の少なくとも1つでは無理数となるという定理です。一方で、ヴェイユ予想を解決したP.Deligne＊11による種々のゼータ関数の特殊値に関する幾何学的予想や楕円曲線から定まるL-関数（ゼータの親戚）の特異点に関する Birch・Swinnerton-Dyer予想など、特殊値研究は現代数学の深い問題です。
さてApéryは、無理数性の証明にアペリ数という有理数数列を用いました。これは思いつくには困難とみえる不思議なものでした。F.Beukersは、その理由の解明とさらなる無理数性証明へ挑戦し、その背後にある楕円曲線やK3曲面と保型形式の研究を見事なかたちで展開しました。その結果、アペリ数たちが持つ顕著な合同関係式なども示されて、代数的整数論の研究対象となっています。ところでζ_Q(2）、ζ_Q(3）からも、アペリ数と同様な性質を持つ数列が得られます^{（8）~（10）}。また、それらの背後に楕円曲線や保型形式がひそみ、さらにs＝4の場合には、保型形式を一般化した保型積分＊12までもが現れます^（8）。次の発展には（数学においてきわめて重要なラングランズ・プログラム^（11）にも関係して）より広い保型形式の研究が待たれます。

＊7 2012年度のHarocheとWinelandsによる量子系の測定と操作を可能とする画期的実験手法に対するノーベル物理学賞の業績も、こうした流れの中心だと思われます。

＊8 ホイン（Heun）方程式とは４点（0、1、t、∞とできます）を確定特異点に持つフックス型の２階常微分方程式です。ガウスの超幾何（ホイン方程式からreductionできる）と異なり、数学構造には明らかにしてゆくべき点がありますが、さまざまな物理現象の記述に現れています。
＊9 このことは、NCHOに適切なバイアス項を追加すればAQRMの場合にも成り立ちます。
＊10 1 + 14 + 19 + 116 + 125 + … π²6というもの。円周率が現れたことに大きな驚きがもたれました。
＊11 1978年度フィールズ賞。
＊12 アーベル積分の拡張であることからそのように名付けられています。Eichler形式とも呼ばれます。

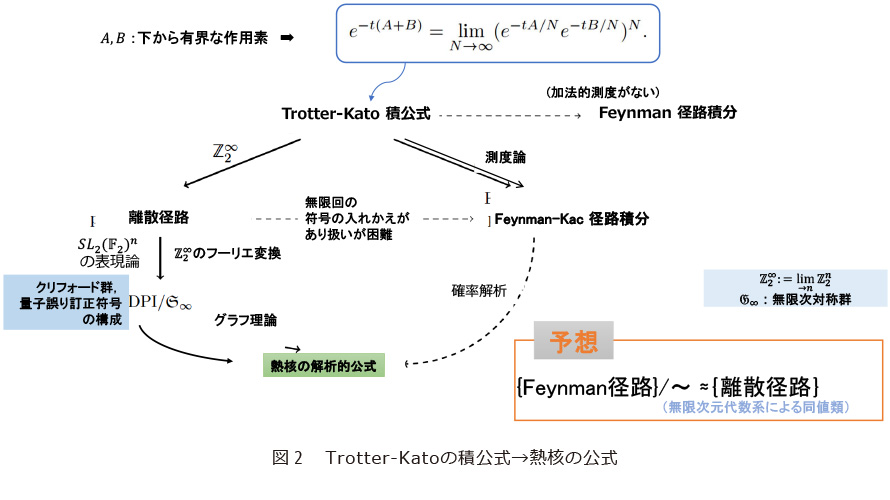
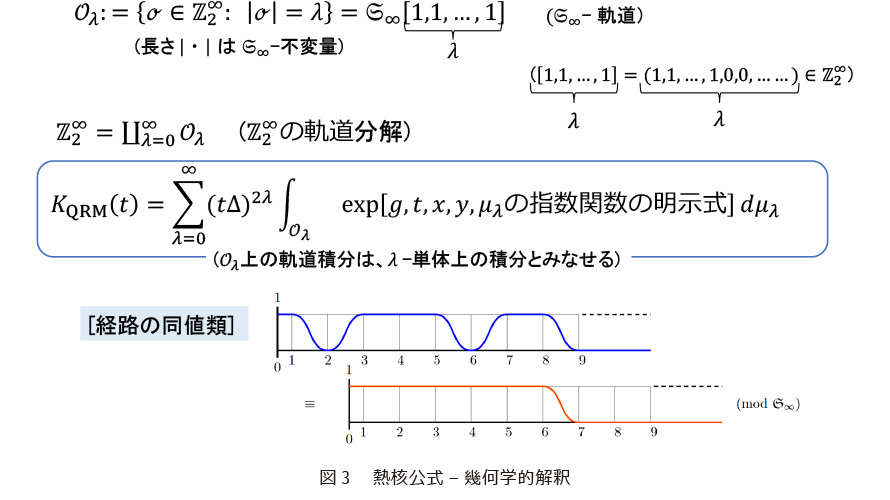
統計力学における分配関数（状態和）の重要性は、それが系の時間発展をよく“知っている”からです。AQRMのスペクトルゼータの研究には、その熱核・プロパゲータ・分配関数の解析的公式を知ることが最重要です。事実、分配関数とスペクトルゼータ関数はメリンの積分変換で1対1に対応しています。しかし、それらの解析的公式を求めることは極めて困難であるとされていました。そのため、物理学者はFeynman経路積分という直感にすぐれた表現形式を用いて種々の近似計算を行い、目的の物理系の理解を深めています。Feynman経路積分は経路が非加算的であり、積分というものの、一般にはそれを定める加法測度が存在しないため、数学的に厳密には扱えません。もちろん、その理解のためのさまざまな検討が今も続いています。私たちは（A）QRMに対して熱核の導出に挑みました＊13。その方法は、成功した結果^（12）からいえば、m次対称群S _mのZ₂^m（m=1,2,…）への作用、Z₂^m上のフーリエ変換とグラフ理論を駆使するものです。ここでZ₂はZ/2Zあるいは2元体 F₂={0,1}です。得られた解析的公式は、熱核がm単体上の初等関数（指数関数の積商）の積分のmに関する級数和です。これは、0と∞を結ぶ離散経路の無限対称群S_∞による同値類全体にわたるS_∞の軌道積分の和（積分）という解釈も可能です（図2）。表現論的には、S_∞の Z₂^∞への作用を既約分解に対応しています。ここで得られた公式は、例えば磁性を持つ微小不純物に対する近藤効果などの理論解析における熱核の行列要素の一部を表す公式や、種々の物理系に対する分配関数の近似式ともよく似ています。こうしたことからは、一般に、Feynman積分の非可算経路たちに作用する無限次元の代数系の存在と、その同値類としての離散経路の獲得という構図も追求すべきでしょう（図3）。
熱核の解析的公式から分配関数が求まり、スペクトルゼータ関数が無限遠点を出る周回積分で表示されます。よって、その全平面への解析接続が得られ、固有値の個数の漸近評価（ワイル法則）が従うほか、特殊値研究に着手できます^（13）。NCHOはQRMの被覆ですので、数論的な性質も伝搬しているはずです。QRMが持つ数論や幾何構造がいかなるものなのか、知るべきことは山積みです。
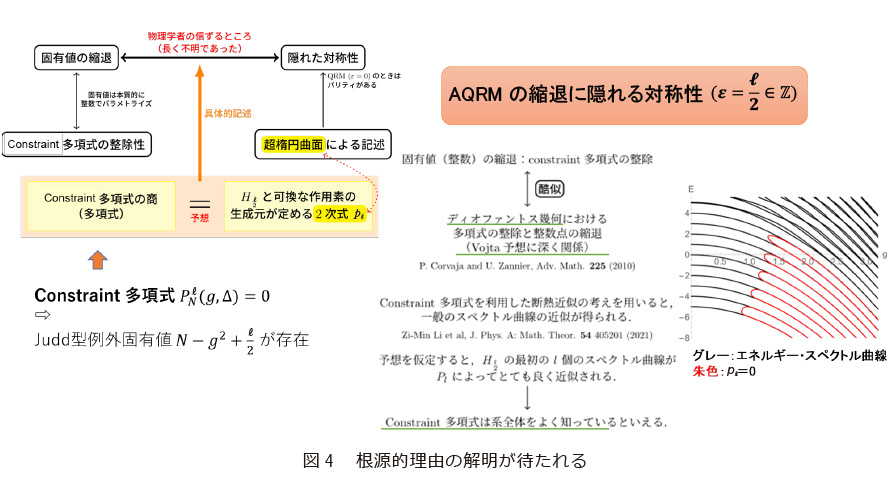
AQRMはハミルトニアン＊14のフリップ項が半整数ℓ/2のときに限り縮退が起こります^{（14）（15）}。ところが、フリップが0でないAQRMはQRMにあるZ₂–対称性（パリティ）を持ちません。一方物理学では、縮退は対称性の存在を示唆すると考えられています^（16）。古典力学とは違い、量子力学においては可積分性の概念が明確ではありません。しかし、古典系のアナロジーから、H_AQRMと可換で非自明な作用素を探す研究^（17）が始まりました。触発された私たちは徹底した解析を行いH_AQRMと可換な作用素を完全に決定しました^（18）。興味深いことに、その可換な作用素の環＊15には自然な生成元Jが定数倍を除き一意的に存在します。しかもJの平方はJ²= p_ℓ（H_AQRM,g,Δ）とH_AQRMの多項式で表示されます。ここでp_ℓはℓ次多項式です。方程式 y²= p_ℓ（x;g,Δ）は超楕円曲線を定めます^（17）。
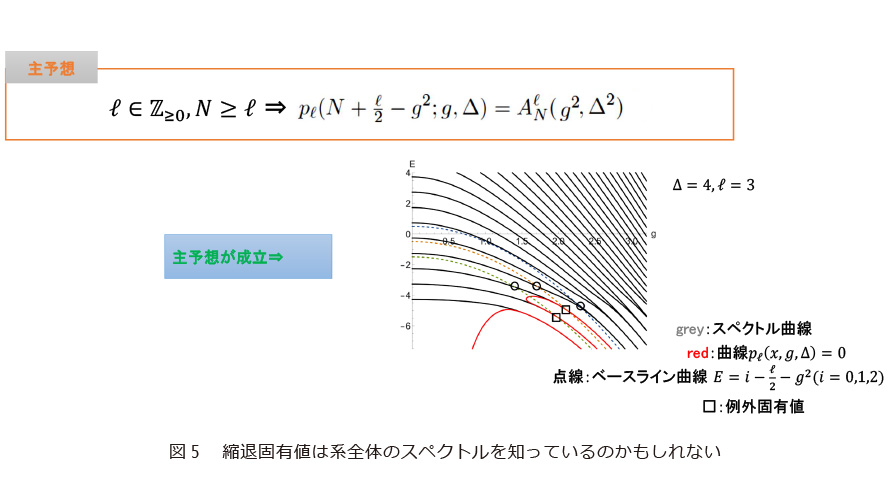
他方、AQRMの縮退固有値は、正整数Nを用いてN±^ℓ/2+g²のかたちです。N、ℓを固定すると（g²,Δ²）はホイン方程式から定まる制約多項式P_N＋ℓ^{（−ℓ/2）}（g²,Δ²）とP_N^（ℓ/2）（g²,Δ²）の共通零点となります。実際、P_N^（ℓ/2）（g²,Δ²）はP_N＋ℓ^{（−ℓ/2）}（g²,Δ²）を割り切り、商となる多項式をA^ℓ_N（g²,Δ²）とすればその正値性も分かります^（13）（図4左）。
数値計算からA^ℓ_N（g²,Δ²）=p_ℓ（N+ℓ/2−g²,g,Δ）（ℓ≦6）が分かります。これが一般に成立していれば、“縮退の背後の隠れた対称性”は明確です（図4）。ただし証明の手立てがなく、予想のままです^（19）（図5）。しかしこの予想は、そのかたちがディオファンタス幾何の定理^（20）＊16に酷似しています。そのため、証明の糸口がそこに発見できるかもしれません。また、AQRMの縮退固有値は有限個であると予想しています。未解決ですが先の予想に重ねると、ここにはモーデル予想＊17との形式的類似点も見出せます。

＊13　Trotter-Katoの積公式が熱核導出の出発点です。Feynman経路積分を形式的に導くのにはこの積公式が有用です。
＊14　AQRMのハミルトニアンはH_AQRM=[光子場]＋[２準位原子]＋[相互作用項]＋[フリップ項（実数で与えられる）]のかたちをしており、H_AQRMのフリップ項は0です。
＊15　整数の全体（整数環）、多項式の全体（多項式環）など、割り算以外、加減乗では閉じている代数系です。
＊16　この定理は著名なヴォイタ予想に深く関係したものです。なお、ヴォイタ予想はモーデル予想の高次元化とも位置付けられABC予想とも深くかかわりを持つものです。
＊17　有理数体上で定義された1よりも大きな種数（穴）を持つ曲線は、有限個の有理点しか持たないであろうという予想です。1983年にファルティングスにより証明されました。

数学を特徴付ける言葉をいくつか拾います。まずはピタゴラスによる“万物は数”。現代社会を席巻するビッグデータ、AI（人工知能）を彷彿させます。万能の天才レオナルド・ダ・ビンチは“工学は数学的科学の楽園である。何となればここでは数学の果実が実るから”と述べています。ガリレオ・ガリレイによる“宇宙は数学の言葉でかかれている”はあまりにも有名です。また、ウィグナーによる“自然科学における数学の不合理ともいえる有効性”は見事な指摘です＊18。
数学研究は作曲に似ている点がありますが、スコアからシンフォニーが再現されるような、数学論文を音楽のように奏でる仕組みがなかなか見つかりませんでした。しかし近年、機械学習・AIなどが生み出す数学の活用が生まれました。研究の動機は多様ですが、好奇心だけで進める純粋数学を含み、今や基礎数学と応用数学が見事な協奏を奏でる機会が到来したかのようです。新たな“数楽”が生まれることを願い本稿を閉じます。

＊18　Eugene Wigner（1902-1995: 1963年ノーベル物理学賞受賞「原子核と素粒子の理論における対称性の発見」）による1960年に公開された講演録。

■参考文献
（1）　A. Parmeggiani and M. Wakayama: “Oscilla­tor representations and systems of ordinary differential equations,”PNAS, Vol. 98, pp. 26-30, 2001.
（2）　T. Ichinose and M. Wakayama: “Zeta func­tions for the spectrum of the non-commuta­tive harmonic oscillators,” Comm. Math. Phys., Vol．258, pp. 697-739, 2005.
（3）　D. Braak: “Integrability of the Rabi Model,” Phys. Rev. Lett., Vol. 107, 100401, 2011.
（4）　布施・吉原・角柳・仙場：“超伝導人工原子と電磁場の相互作用〜強結合のその先へ〜,”日本物理学会誌，Vol. 73, pp. 21-26, 2018.
（5）　若山：“光とゼータ関数の特殊値,”数学通信，Vol. 25, No. 4, pp. 24-52, 2021.
（6）　H. Ochiai: “Non-Commutative Harmonic Oscillators and Fuchsian Ordinary Differen­tial Operators,” Comm. Math. Phys., Vol. 217, pp. 357-373, 2001.
（7）　M. Wakayama：“Equivalence between the eigenvalue problem of non-commutative harmonic oscillators and existence of holomorphic solutions of Heun differential equations, eigenstates degeneration and Rabi model,” Int. Math. Res. Not., Vol. 145, pp. 759-794, 2016.
（8）　K. Kimoto and M. Wakayama: “Apéry-like numbers for non-commutative harmonic os­cil­la­tors and automorphic integrals,” Ann. Inst. Henri Poincaré - D, （in press） - arXiv:1905.01775, 2020.
（9）　L. Long, R. Osburn，and H. Swisher: “On a conjecture of Kimoto and Wakayama,” Proc. Amer. Math. Soc., Vol. 144, pp. 4319-4327, 2016.
（10）　J.-C. Liu: “A generalized supercongruence of Kimoto and Wakayama,” J. Math. Anal. Appl., Vol．467, pp. 15-25, 2018.
（11）　R. Langlands:“Letter to André Weil,” https://publications.ias.edu/rpl/paper/43
（12）　C. Reyes-Bustos and M. Wakayama: “The heat kernel for the quantum Rabi model,” Adv. Theor. Math. Phys., (in Press)- arXiv:1906.09597, 2020.
（13）　C. Reyes-Bustos and Masato Wakayama：“Heat kernel for the quantum Rabi model: II. Propagators and spectral determinants,” J. Phys. A: Math. Theor., Vol. 54, pp.115202-115231, 2021.
（14）　K. Kimoto, C. Reyes-Bustos, and M. Wakayama: “Determinant expressions of constraint polynomials and the spectrum of the asymmetric quantum Rabi model,” Int. Math. Res. Not., pp. 9458–9544, 2021．
（15）　M. Wakayama: “Symmetry of asymmetric quantum Rabi models,” J. Phys. A: Math. Theor., Vol. 50, pp. 174001-174020, 2017.
（16）　S. Ashhab: “Attempt to find the hidden symmetry in the asymmetric quantum Rabi model,” Phys. Rev. A, Vol. 101, 023808, 2020.
（17）　V. Mangazeev, M. Batchelor，and V. Bazhanov: “The hidden symmetry of the asymmetric quantum Rabi model,” J. Phys. A: Math. Theor., Vol. 54, 12LT01, 2021.
（18）　C. Reyes-Bustos, D. Braak, and M. Wakayama: “Remarks on the hidden symmetry of the asymmetric quantum Rabi model,” J. Phys. A: Math. Theor.，Vol．54, pp. 285202-285215, 2021.
（19）　C. Reyes-Bustos and M. Wakayama: “Degeneracy and hidden symmetry—an asymmetric quantum Rabi model with an integer bias,” Comm. Number Theor. Phys. （in Press） - arXiv:2106.08916, 2021.
（20）　P. Corvaja and U. Zannier: “Integral points, divisibility between values of polynomials and entire curves on surfaces,” Adv. Math., Vol. 225, pp.1095-1118, 2010.