前回お話をしたのが2020年ですね。当時はシリコンバレーで、NTT Research, Inc.のCryptography and Information Security Laboratories（CIS研）所長として、マネジメントをする立場からCIS研で手掛ける暗号、ブロックチェーンといったテーマについて、NTT Research, Inc.はどのような研究所かも含めてお話しさせていただきました。2022年7月に帰国して、NTT社会情報研究所（社会研）で暗号理論を研究しています。NTT Research, Inc.在籍中の2021年夏には、CIS研のマネジメントを行う傍らインターンシップの学生を受け持ち、アダプター署名というブロックチェーン上の取引で使われる暗号をテーマに研究指導を行ってきました。
さて、今回お話しするのは大枠では暗号とも関連する研究ですが、「複雑性」という分野についての研究です。
動物や植物といった生物を構成する細胞等ミクロな世界まで追っていくと、非常に複雑な構造になっています。また、宇宙もビッグバン直後の単純な姿から複雑なかたちに進化してきたことが知られています。こうして周囲を見渡すと、実は複雑なものがあふれています。「複雑性」は、こうした世の中で複雑だといわれている物事に対して、統一的な見方で定義し、定量化していくことを科学としてとらえる研究です。複雑系という研究分野は30年以上前からあり、多くの優れた研究成果はあるものの、その基礎となる「複雑性」についての研究はあまり進展していません。この分野について、私は暗号の研究を行うかたわら考察を重ねていたのですが、最近、「複雑性」の定量的な定義に関する論文を『Complexity』という学術誌で発表しました^（1）。これは複雑さが持つ3つの重要な特徴（後述）すべてを同時にとらえた世界初の定義です。
この「複雑性」の研究にも暗号理論の考え方や概念が役立っており、例えば暗号におけるゼロ知識証明の理論に関連して導入された知識複雑度の概念は今回の定義を導く際に1つのヒントを与えてくれました。

まず、複雑さの問題とは何かをお話しします。米国の科学者、ウィーバー（Weaver）は科学的な問題を「単純な問題」、「組織化されていない複雑な問題」、そして「組織化された複雑な問題」の3つに分類しました。
「単純な問題」とは力学でビリヤード台の上の数個の球の動きを正確に解析して予想するような問題です。「組織化されていない複雑な問題」とは、巨大なビリヤード台の上を数100万個の球が相互に（そして台を囲む壁に）ランダムにぶつかり合って転がっており、その平均的なふるまいを統計力学で解析・予測するような問題のことをいいます。そして、「組織化された複雑な問題」は、多くの細胞が相互に関連して全体として1つの生命体を形づくっている生物や生態系、人工物などの組織化された複雑なものを対象とする問題と定義しました。したがって、複雑な問題は組織化されたものと、組織化されていないものに分類されます。
そして、この「複雑な問題」において科学としてもっとも基本的で重要な概念は、複雑さの定量的定義です。物理系における「組織化されていない複雑さ（乱雑さ）」の定量的な定義は、熱力学や統計力学で登場するエントロピーとして確立しています。また、情報源（確率分布）の「組織化されていない複雑さ（乱雑さ）」の定量的な定義はシャノン・エントロピーとして確立されました（この2つのエントロピーは定数を除き基本的に同じです）。
一方、「組織化された複雑さ」の定量的定義においては、多くの試みがなされてきたにもかかわらず、広く合意された定義は現在のところ存在しません。この定義の困難さは、「組織化された複雑さ」が私たちの持つ感覚に多分に依存するもの（もしくは、私たちのような知的生物によって認識できるもの）であり、単なる乱雑さのようなものとは大きく異なることにあります。さらに、これらの試みは、確定的系列あるいは確率分布のいずれかを対象としたものであり、両方を同時に対象とする定義はまだありません。

そこで私は「組織化された複雑さ」の定義の対象はどうあるべきかを検討しました。
まず、複雑さの対象は私たちの周りにあるすべてのものであって、宇宙の中の星々や銀河、生物、生態系、人工物、さらには人類社会などを含みます。それらを私たちが認識するには、望遠鏡、顕微鏡やさまざまな観測装置、電子機器を通じた観測という手段を経由するしかありません。私たちは実際に物を手にすることで直接その存在を認識しますが、それも人間の五感（センサ）を通じて得た観測データを脳で処理してその存在を解釈、認識しているという意味で、観測により得た結果です。つまり、私たちはすべてのものを何らかの観測データにより認識しているのです。
一般に物理現象の観測データ（確定的系列）の源（情報源）は「確率的な分布」であり、観測データは、その分布にしたがってランダムに選ばれた値です。したがって、「組織化された複雑度」の対象は情報源からたまたま選ばれた観測データ（確定的な値）ではなく、情報源そのもの、つまり「確率的な分布」とするのが自然です。その結果、「組織化された複雑度」の対象は「確率的な分布」（情報源）であるべきであると考えました。確定的な系列は、確率的な分布の特殊ケース（1つの値だけが確率1で発生している確率分布）の場合もあるため、そのような確定的系列も対象となります。

例えば、チンパンジーに計算機のキーボードを与えて自由にキーを叩かせたときの文字列（アルファベット1000文字）と、シェークスピアの戯曲の台詞の文字列（アルファベット1000文字）は、いずれも確定的な文字列ですが、両者の情報源を比較すると、その複雑さの違いが鮮明に見えてきます。チンパンジーの場合、情報源はランダムな1000文字のほぼ一様な分布（単純な分布）となり、その「組織的な複雑さ」は最低レベルだということが分かります。一方、シェークスピアの台詞の場合、その情報源はシェークスピアの頭の中にあるいくつかの表現の候補の確率分布であり、シェークスピアが頭に浮かんだいくつかの表現から選ぶとき（いくつかの表現候補の複雑な確率分布）やシェークスピアが迷いなく選んだ1つの表現となるとき（1つの複雑な文字列が確率1で起きる確率分布）などがあり、いずれも複雑な分布となるためその「組織化された複雑さ」は大変大きくなります。
「組織化された複雑さ」をシェークスピアの台詞の場合で考えると、複雑さにはいくつかの異なった特徴があることに気付きます。対象（情報源）が確率分布であるため、確率分布のパターンとしての複雑さ（確率的特徴）があり、戯曲を書くために必要な知識（言語、歴史文化など）およびそのストーリーなど記述量としての複雑さ（記述的特徴）があります。さらに、書きたいことが決まったときにそれを表す適切な文学的表現を選ぶ場合には頭の中でいろいろと考えますが、そのような言語表現を選ぶことはグラフの問題としてとらえることができ、適切な表現を選ぶことはグラフの問題を計算することに相当するというような計算量に関する複雑さ（計算的特徴）があります。つまり、「組織化された複雑さ」には確率的、記述的、計算的という3つの特徴があり、これを定義するためには、これらの特徴をすべて同時にとらえる必要があります。もちろん、複雑度の値は計算可能であるべきで、「組織化されていない複雑な問題」（チンパンジーの例）や「単純な問題」の複雑度は小さくなくてはなりません。
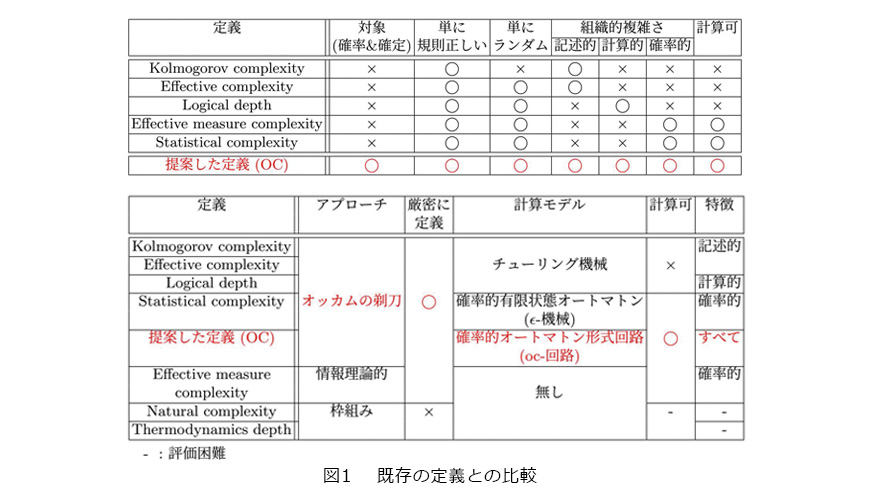
従来の定義の問題点は、①複雑さが持つこの3つの特徴（記述的、計算的、確率的）のいずれか1つだけしかとらえておらず、②対象を確定的系列か確率的分布かのいずれかとしており、両方を同時にシームレスに対象とすることはできませんでした。そして、③いくつかの定義はその複雑度が計算不可能であり、④いくつかの定義は厳密に定義されていなかったのです（図1）。
そこで、私はこれら4つの問題点をすべてクリアする新たな「組織化された複雑さ」の定量的定義（組織複雑度:OC）を実現することをめざし、それを達成することができました。

私の複雑度の定量的定義（OC）の基本的考え方は、対象（情報源:確率分布）をシミュレーションする最小の確率的オートマトン形式の論理回路（oc-回路）のサイズで定めるということです（「最小の」サイズとすることは「オッカムの剃刀」原理です）。複雑さの記述的および計算的な特徴をとらえるためには何らかの計算概念を用いる必要がありますが、従来の定義ではチューリング機械（計算機）を用いていました。その代わりに私の定義では、（確率的オートマトン形式の）回路を用いています。その理由は、回路だと3つの特徴を回路のサイズで同時にとらえることができるからです。また、チューリング機械を用いた定義が計算不可能になるのに対して、回路を用いることで計算可能とすることができます。その結果、①複雑さが持つこの3つの特徴（記述的、計算的、確率的）を同時にとらえることができる、②確率分布と確定的系列をシームレスに対象とすることができる、③計算可能、④厳密に定義、⑤「組織化されていない複雑な問題」や「単純な問題」の複雑度は小さい、という従来の定義の問題点をすべてクリアし、求められる要件をすべて満足する複雑性の定量的定義（OC）を実現することができました（図1）。
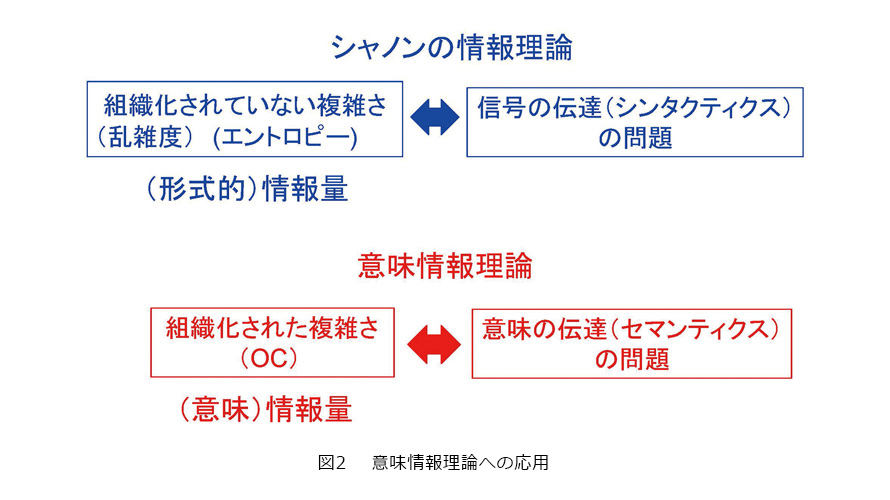
この結果は、機械学習や人工知能の理論的基盤、組織的複雑さを持つアルゴリズム、ネットワーク、計算量・通信量の限界や平均の解析、意味情報理論等に応用できます。例えば、信号の伝達（シンタクティクス）の問題に対してエントロピー（組織化されていない複雑さ）を情報量として扱うシャノンの情報理論に対して、ここで定義した組織複雑度（OC）を（意味）情報量として意味の伝達（セマンティクス）の問題を扱う意味情報理論が構築できると考えています（図2）。

情熱と知識を大切に、目の前に立ちはだかる問題や長年解けていない問題を解決しようとするのが研究者であると私は思っています。いうまでもなく、世界はインターネットの普及によってボーダーレスとなりました。研究者にとっては世界を見据えて研究に臨むことが重要になります。
ご存じのとおり、私はシリコンバレーの中の研究所で優秀な研究者たちと仕事をしてきました。この研究所では世界でトップレベルの優秀な研究者が集まって切磋琢磨していることから、エネルギーに溢れています。博士課程在籍中の研究者もいましたが、彼らも相当にアグレッシブです。こうした研究者たちのパワーを肌で感じてきた経験から、日本の若い研究者や研究者をめざす大学院生もそのような研究に対する熱量が大切だと思っています。世界中のパワフルな研究者と競い、世界にインパクトを与える研究を成し遂げようとしたら、寝ても覚めてもそれを追究し続けられるほどのエネルギーや情熱が必要になるということです。
一方で、日本から世界で活躍する研究者を輩出しようとするならば、彼らを支える体制や構造的な改革も迫られてくるかもしれませんね。例えば、米国では博士号を取得した研究者は通常ポスドクからスタートします。ポスドクは研究者の助走期間的な位置付けではなく、自分のやりたいテーマを携えて、1人の独立した研究者として研究に専念します。任期がきても、業績を上げていればキャリアアップした研究者として（競争で得た）新たな地位で研究を続けます（これは理論系の研究の場合で、実験系では違うようです）。1人の独立した研究者である以上、先生に学ぶというよりも、仲間と切磋琢磨しながら自分を成長させることのほうが多くなりますから、世界各国の優秀な研究者が集まるような環境、そして研究する場所に依存せず若いときから1人の研究者としてキャリアアップできる環境を整備することも求められているように思います。
とはいえ、研究者や研究者をめざす者は環境のせいにせずに、自ら選んで、研究できる場所、切磋琢磨できる場所へ身を置くことも重要です。海外の研究機関に身を置くのもその1つの手段です。この場合、海外であるがゆえに言語や文化の違いから、現地の生活がストレスになることもあります。これはハンディキャップになるかもしれません。慣れによりある程度は時間が解決してくれることもありますが、自ら海外へ出ていくときは、こうしたストレスを跳ね返すくらいの熱意を持って研究に臨んでほしいと思います。

■参考文献
（1）　https://www.hindawi.com/journals/complexity/2022/1889348/