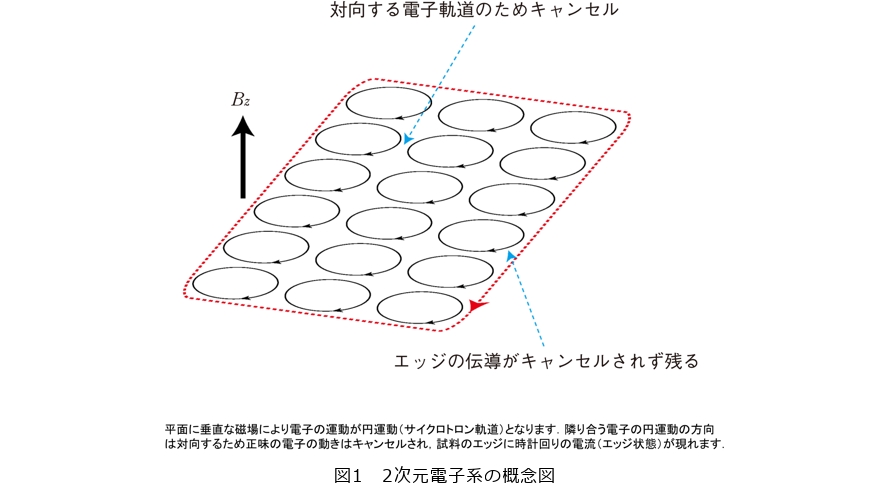
伝播する方向が一方向のみ許される場合、例えば時計の針のように反時計回りがないという状況を光だけでつくり出すのは難しいものです。光の場合、散乱体があると後方に反射して、その伝播方向が反転するからです。光の直進性を活用するためには、例えば光ファイバのように物質による全反射を利用します。すなわち光の操作性を高めるには、光と物質の相互作用をうまく活用する必要があります。他方、光を生み出す元となる物質中の電子に関しては、そのような向き付けられた伝播が2次元電子系＊1に面直方向に強磁場をかけることで実現できます。図1に示すように、磁場により個々の電子はサイクロトロン運動と呼ばれる円軌道をとり、磁場のベクトル方向に依存する向きを周回しますが、電子がたくさんあるような状況では、微視的視点で容易に想像できるように隣り合う電子の円軌道は対向する伝播方向になるため、巨視的視点ではキャンセルし、たくさんの電子が協調的につくり出す実質的な電流は、試料の端（エッジ）にだけ残ります。これは、エッジ状態と呼ばれ、端に沿った伝導チャネルを形成します。エッジ状態の伝播方向は加える磁場の方向によって時計回り、または反時計回りどちらかになります。では、そのような向き付けられた電子の運動を強制的に励起するとどうなるか、これは1980年代から研究されているテーマですが、電子と電磁場のハイブリッドであるプラズモンが励起して、試料のエッジを一方向に伝播します。今の場合の励起状態は、外部磁場によってつくられるエッジ状態のプラズモンなので、エッジマグネトプラズモンと呼ばれます。

＊1　2次元電子系：炭素一原子の厚みしか持たない究極に薄い平面シートであるグラフェンは、その2次元平面内しか電子は存在しないため、2次元電子系の代表例です。

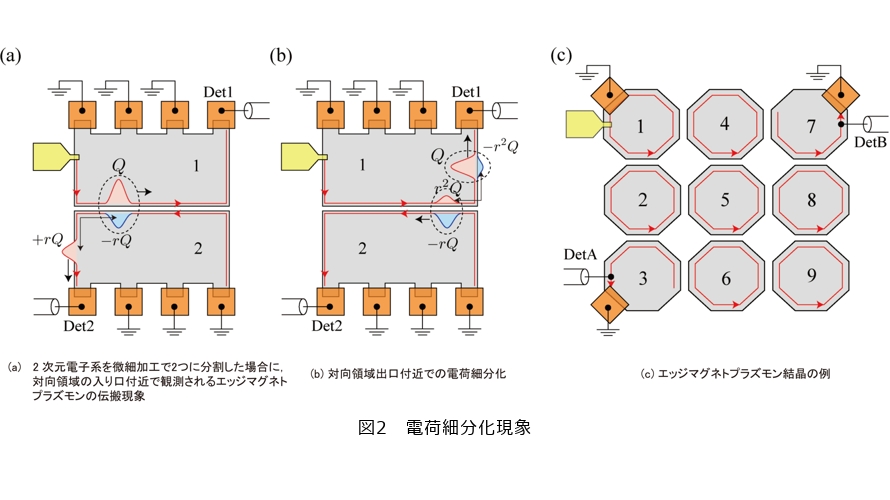
そこで、2つの2次元電子系を用意する、もしくは、エッジマグネトプラズモンが周回する1つの2次元系を微細加工技術で2つに分割した場合、どのようなことが生じるかというのは興味のあるテーマです。図2に示したように試料を2つに分割し、上の試料を1、下の試料を2とします。試料1、2の端にはエッジマグネトプラズモンが励起可能で、反時計回りに伝播すると仮定します。したがって試料1と2の間の溝の部分では、（道路や電車路線のような）対向するチャネルがつくられ、溝の距離が十分に近いと相互作用が働きます。相互作用は電磁気学的（クーロンポテンシャル）なもので、図2（a）に示したように、試料1でエッジマグネトプラズモンを励起して、それが対向領域に達すると、何もなかった下の試料2に電荷密度の濃淡（プラス電荷とマイナス電荷の対）をつくり出します。領域1で励起されたエッジマグネトプラズモンが電荷Qを持っているとすると、領域2の対向領域の入り口で対生成される電荷ペアは±rQと書けます。ここでrは結合定数と呼ばれる0から1の数で、領域1と2の相互作用の強さを表します。rQの電荷を持つエッジマグネトプラズモンは対向領域には入らずに領域2のエッジを反時計回りに進み測定器2で検出されます。一方、−rQのほうは領域1を伝播する電荷Qを持つエッジマグネトプラズモンに引きずられて、領域2の正規の伝播方向とは逆に、対向領域の出口まで伝播します。その際、伝播の速度は、相互作用により、通常のエッジマグネトプラズモンの速度を1-r1+r倍した低速度で与えられます。これは対向領域の“屈折率”が1+r1-rで与えられていることに相当します。この複合パルスが対向領域の出口に達すると、領域2の−rQはパートナーによる引力を失い、正規の伝播方向へと反転しますが、その際、図2（b）に示すように、領域1に電荷±r²Qのペアを生成し、再度複合パルスがつくられて、伝播します。このようにパルスの時間発展を追うと、次第に電荷が細分されるので、電荷の細分化現象と呼ばれます。大変興味深い現象ですが、NTTの実験で検証されました^（1）。少々意外ですが、パルスではなく角周波数ωで与えられる交流の入力に対しては、通常の薄膜を光励起する場合でお馴染みの反射率や透過率が計算されます。すなわちエッジマグネトプラズモンは確かに光の振舞を併せ持っている光と電子のハイブリッド状態なのです。

私が取り組んでいる研究は、前述の問題の延長です。1つの2次元半導体を微細加工技術で多数の要素に分割した場合、すなわち、半導体の“結晶”状ネットワーク（例えば図1（c）のようないくつかの“原子”からなる結晶）を考えた場合にどのような現象や機能性が発現するか、という問題です。このような問題を取り上げたのは、研究発展の自然な方向性である〔例えばナノカーボンの研究ではC60フラーレンから筒構造のナノチューブ、平面系グラフェンと六角格子（ベンゼン環）のネットワーク周期性が上がっていった研究歴史があります〕、というだけのモチベーションで行うのではありません。むしろもともとの強磁場におかれた2次元半導体の電子的性質を、より光に近い描像で理解し、新方面に活用しようという方向性もあります。例えば仮想的に分割の程度をサイクロトロン円運動の直径程度にとれば、状況は量子ホール系のプラズモン光学的シミュレーションとも考えられます。ネットワークのエッジには、どのような条件（結合の強さや結晶の形）のもとでエッジマグネトプラズモンが現れるかは、興味のある問題の1つです。また、量子ホール効果には整数と分数の2種類がありますが、それらの違いをエッジマグネトプラズモンの観点で理解できると考えています。整数の起源は単一電子描像で、不純物による散乱の効果として、また、分数の起源は電子間相互作用による多体効果であると考えられており、エッジマグネトプラズモン結晶の場合、散乱体はネットワーク中の欠陥、また結合定数rが電子間相互作用の代替パラメータとなります。
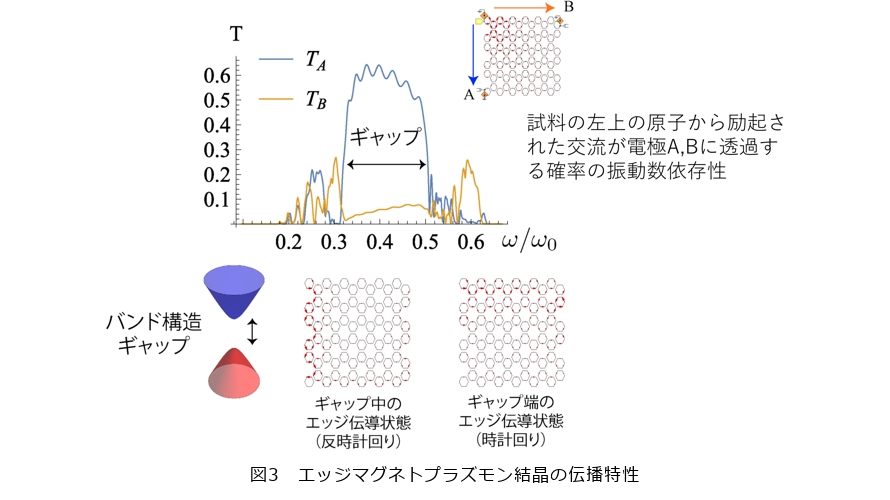
まず、ドメイン結晶の中を伝わるエッジマグネトプラズモンの伝播特性を知るために、そのエネルギーバンド構造を計算しました^（2）。計算の詳細は割愛しますが、エッジのない周期的なネットワークに対して転送行列法を用いました。バンド構造は、結晶の状態を理解するうえで便利なもので、波長に対して固有振動数をプロットしたものです。すべての波長に対して固有振動がない場合、エネルギーギャップがある、といいギャップの中の振動数では伝播する状態がありません。図3に示した“原子”の形が六角形で、ハニカムネットワークを持つ場合の計算結果では確かにギャップのあるバンド構造が得られました。2つの円錐の間のギャップの大きさは相互作用rとともに大きくなる傾向があり、相互作用に起因したエネルギーギャップであることが分かります。もともとの試料を分割する前の試料で、エッジマグネトプラズモンが現れるのはサイクロトロン軌道（図1）が量子化＊2されることによって生成されるエネルギーのギャップの中であり、このギャップは相互作用によってつくられたものではありません。したがって、エッジマグネトプラズモン結晶のギャップはもともとのエッジマグネトプラズモンとは起源が異なるものです。
エッジマグネトプラズモン結晶においてもエネルギーのギャップが現れることが分かりましたが、そのギャップの中ではネットワークのエッジを伝播するエッジモードが存在するかどうかは（周期的でエッジのない系を仮定して計算した結果得られた）バンド構造だけからは分かりません。より詳細な解析をすると、図3に示すようにエッジモードがあることが分かります。すなわち、エッジマグネトプラズモン結晶にも“エッジマグネトプラズモン”が存在するということが分かります。興味深い点としてバンドギャップの端のあたりの周波数に、通常のエッジの伝播方向とは逆向きに進むモードが現れることも分かります。実は、分数量子ホール効果ではエッジ状態の伝導が双方向になる場合もあることが知られています。“原子”間の相互作用というのを考えたことにより、多体効果によって生じる分数量子ホール効果も計算で取り入れられて、逆方向に伝播するモードが現れたためと解釈することができます。

＊2　量子化：粒子の数のように1つ、2つと離散的な値をとること。半分の粒子というのは存在しません。同じ考えはエネルギーなどに適用されます。

2次元電子系の物性は、近年では数学のトポロジーと結び付くなど、基礎から応用へ幅広く発展している分野で、そこで得られた知見を光の操作性向上に利用しない手はないのです。しかし、一般的に電子状態のエネルギースケールが光（例えば通信波長帯）のそれと大きくかけ離れているため、両者を直接的に結び付けることは難問で、新しいアイデアを必要とします。光と電子の振舞がどのようにすれば融合して、新しい機能性を出すのかは光電融合として多くの研究者の関心事ですが、私は電子と光のハイブリッド状態であるプラズモンをヒントに、そのようなアイデアを模索中です。今回提案しているエッジマグネトプラズモン結晶は1つのアイデア候補になるかもしれません。また、光の強度が小さい場合、光の量子（フォトン）が示す量子力学的な振舞にも多くの関心が集まっていますが、エッジマグネトプラズモンの量子力学も古くから研究されているテーマで、今後の課題の1つとしてエッジマグネトプラズモン結晶の量子場の理論＊3があります。

＊3　量子場の理論：時間・空間の中で、どのように粒子（光子、電子など）が生成・消滅・伝播されるかを予測する計算手法の総称です。

■参考文献
（1）　P. Brasseur, N. H. Tu, Y. Sekine, K. Muraki, M. Hashisaka, T. Fujisawa, and N. Kumada：“Charge fractionalization in artificial Tomonaga-Luttinger liquids with controlled interaction strength，”Phys. Rev. B，Vol. 96，No.8，081101(R) ，August 2017.
（2）　K. Sasaki：“Band structures of edge magnetoplasmon crystals，”Phys. Rev. B, Vol.105, No.7，075312，Feb. 2022.