現代社会で使用されているコンピュータと同様に、量子コンピュータにおいても、ハードウェア上で走らせるソフトウェア（計算手順＝アルゴリズム）の良し悪しが計算性能を大きく左右します。この意味で、量子アルゴリズムは、量子コンピュータの有用性を決定付ける中核技術といってよいでしょう。

私たちの日常生活に密接に関係している問題のほとんどは、量子の概念とは一切関係のない問題（古典問題）です。もし、量子コンピュータを用いて、既存の計算原理に基づくコンピュータ（＝古典コンピュータ）よりも圧倒的に速く、古典問題を解くことができれば、私たちの生活・社会に大きなインパクトを与えられると期待されています。
これまでの研究により、量子コンピュータを用いて計算を高速化できる古典問題が次々と明らかになってきました^（1）。特に、衝突発見問題は、量子ウォークに代表される、さまざまな量子アルゴリズム技術を生み出す際に中心的な役割を演じました。ここで生み出されたアルゴリズム技術を基礎として、行列乗算など応用上重要な多くの古典問題に対する高速量子アルゴリズムが考案されました。以降では、衝突発見問題を例に、量子アルゴリズム技術を、少し異なる観点、すなわち、情報通信の安全性の観点から考えてみます。
高い計算能力を期待されている量子コンピュータは、良いことに使われるばかりでなく、「暗号を破る」という悪いことにも利用されるおそれがあります。このため、近年、量子コンピュータによる強力な攻撃を考慮した、暗号の安全性評価が求められています。この安全性評価を行うためには、攻撃者の攻撃能力を知る必要があり、したがって、具体的な攻撃手法を考える必要があります。量子コンピュータを用いた攻撃手法とは、量子アルゴリズムにほかなりません。
私たちは、これまで培ってきた量子アルゴリズムの基礎技術を基に、暗号の中核技術であるハッシュ関数に関して、量子コンピュータを用いた最高速攻撃手法を考案しました^（2）。
ハッシュ関数とは、長いデータを入力として、短いデータを出力する関数です。ただし、暗号では、出力データから入力データの推測が難しいものが使われます。ハッシュ関数の応用範囲はとても広く、例えば、電子署名や公開鍵暗号など、私たちの生活に密着したものにも使われています。
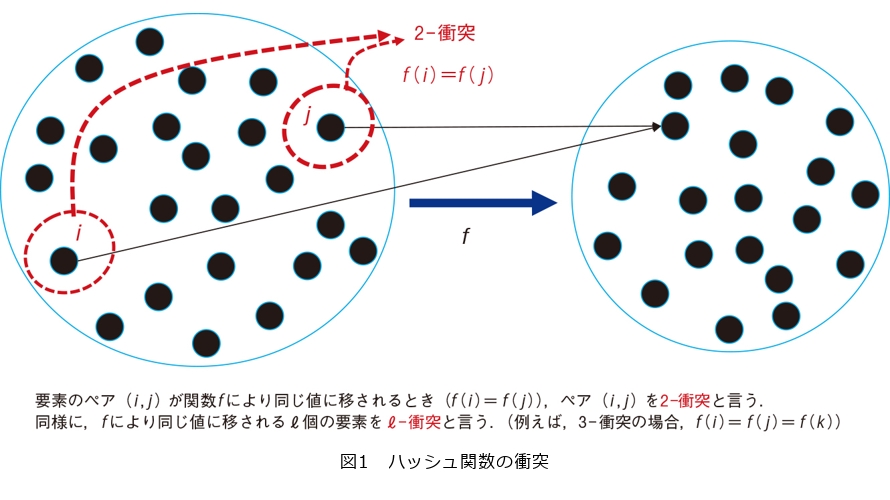
では、ハッシュ関数に対する攻撃とは何か、ということを「衝突」という概念を用いて説明します。ハッシュ関数fにより同じ値に移される複数の要素を衝突と言います（図1）。一般に、ハッシュ関数fにより同じ値に移されるℓ個の要素をℓ-衝突と言います。また、ℓを衝突の多重度と言います。例えば、図1の場合、2つの要素i,jがfによって、同じ値に移されているので、（i,j）は衝突であるといえます。
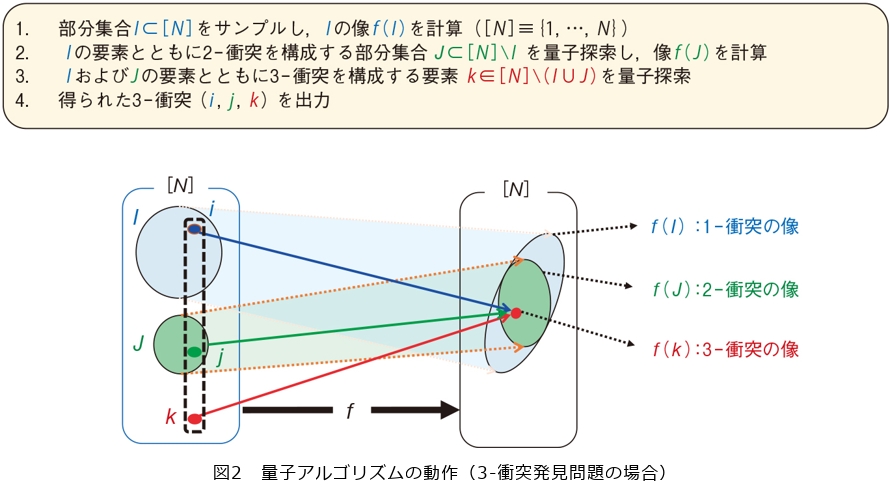
衝突を発見できると、例えば、同じ認証データを持つ別の文書に改ざんできてしまう可能性があります。このため、ハッシュ関数fを暗号に使うためには、衝突発見の困難性（=膨大な時間を要するかどうか）を評価する必要があります。この評価のために、衝突を発見するアルゴリズムが必要となります。私たちは、任意の多重度ℓに対して、ℓ-衝突を発見する高速量子アルゴリズムを考案しました（図2）。提案アルゴリズムの計算速度は、すべての多重度において、理論限界を達成しており、これにより、ハッシュ関数を用いた暗号の、より正確な安全性評価が可能になると期待されます。
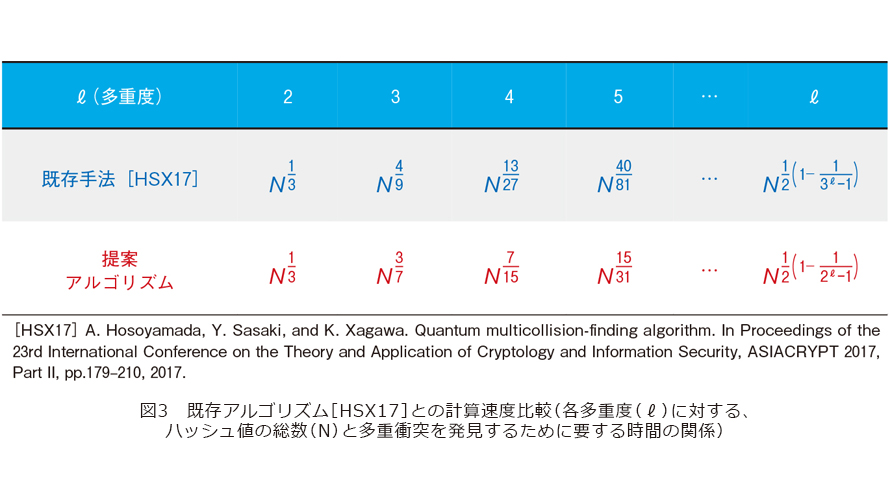
図3は、各多重度（ℓ）に対する、ハッシュ値の総数（N）と多重衝突を発見するために要する時間の関係を既存の手法と比較したものです。数学的には、Nは、ハッシュ関数の値域のサイズです。多重度2の場合の計算時間が両手法で同じ理由は、既存手法が理論限界を達成しているからです。多重度3以上では、すべての場合において、既存手法より高速になっています。
具体的な数値例を考えてみます。多重度ℓ＝3、ハッシュ値の総数Nが2000bit値の場合、既存手法の計算時間に比べ、提案手法の計算時間は10億倍程度高速になっています。
量子アルゴリズムを高速に実行するには量子回路レベルでの最適化が必要です。次に量子回路の最適化技術に関する成果を紹介します。

光子や電子など、どのような量子系についても、その状態の変化の様子はユニタリ行列で表現されます。それゆえに、量子アルゴリズムから量子コンピュータに送られる「命令」も本質的にはユニタリ行列のかたちで与えられます。例えば、素因数分解を効率的に解くことで知られるShorのアルゴリズムに登場する重要な命令として、量子フーリエ変換と呼ばれるユニタリ行列が挙げられます。ところが、雑音に弱いという量子系の特性から、それらのユニタリ行列（が表現する状態変化）を完全な精度で実現することはできません。そこで通常は、高精度に実現できる数種類のユニタリ行列（これらを基本ゲートと呼びます）を適切な順序で実行することで所望のユニタリ行列を実現します。したがって、（a）基本ゲートの総数＝（b）命令数×（c）1命令分のユニタリ行列を実現するための基本ゲート数、という関係が成り立ちます。量子アルゴリズムの実行時間はおおむね（a）の基本ゲートの総数で見積もることができるので、総数を減らすための最適化手法が数多く提案されてきました。それらは大まかに、各々のアルゴリズムの構造を活かして （b）の命令数を削減する手法と、アルゴリズムの構造とは独立に（c）の基本ゲート数を削減する手法に分類することができます。ここで、アルゴリズム設計時に基本ゲートを1つの命令だとみなせば、後者の最適化は不要に思われるかもしれません。しかし、基本ゲートは量子コンピュータをどのような量子系で実装するかによって変わってくることと、個々の量子系に依存しない直感的な命令群でアルゴリズムを設計したいことを踏まえると、後者の最適化が必須となります。
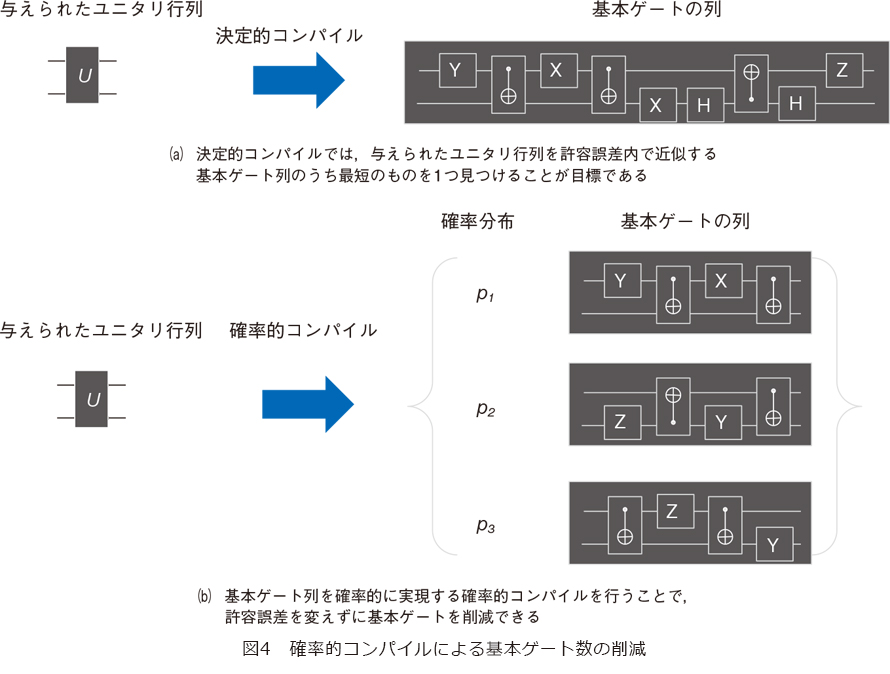
（c）の最適化では、連続自由度を持つユニタリ行列を有限個の基本ゲートの列で厳密に実現するのは不可能なので、許容誤差内で近似的に実現できる基本ゲートの列を探索します（これをコンパイルと呼びます）。適切に選ばれた基本ゲートの十分長い列を用いれば、任意のユニタリ行列を任意の精度で実現できることが知られています。したがって、そのような基本ゲートの列のうち、与えられたユニタリ行列を許容誤差内で近似できるもっとも短いものを出力することが（c）の最適化の目標となります。多くの先行研究ではもっとも短い1つの基本ゲート列を探索する（これを決定的コンパイルと呼びます）ことを目標としていたのに対し、近年、確率的に基本ゲート列を実現する（これを確率的コンパイルと呼びます）ことで、ゲート列の長さを増やさずにユニタリ行列の近似誤差を改善できることが発見されました。これは、同じ許容誤差の下では確率的コンパイルを行うことで、従来の決定的コンパイルと比較してより短い基本ゲート列でユニタリ行列を近似できることを意味します（図4）。しかし、さまざまな関連研究がある一方、確率的コンパイルの限界能力は分かっていませんでした。
今回私たちは、確率的コンパイルが達成し得る近似誤差の理論限界を解明しました^（3）。また、効率的に実行できる確率的コンパイルの手順も考案し、既存の確率的コンパイラと比較して、最小の近似誤差を達成できることを理論的に示しました。いくつかの具体的な例で計算したところ、この確率的コンパイラにより（c）の基本ゲート数を、決定的コンパイラの場合と比較して、50％程度削減できることも分かりました。確率的コンパイルを解析するための理論は、コンパイルにおいて実用的な価値があるだけでなく、今後、古典・量子ハイブリッド型の情報処理を探求していくうえで、幅広い応用が期待されています。
量子アルゴリズムの実行の信頼性を高めるためには、コンパイラで得られた量子回路が実際のデバイスでどの程度正確に実現されているかを検証する必要があります。

量子コンピュータは、雑音等に起因するエラーが発生しやすいという性質があります。発生したエラーに対処するための代表的な2つの手法として、「量子エラー訂正・抑制」と「量子計算の検証」があります。これら2つの手法は、お互いの欠点を補い合う相補的な関係にあります。量子エラー訂正・抑制はエラーが発生した際に訂正または抑制できる代わりに、どのようなエラーがどの程度発生しているのかをある程度知っている必要があります。一方で、量子計算の検証はエラーが未知の場合でも適用可能ですが、エラーを訂正することはできず、量子コンピュータの計算結果にエラーが発生しているかどうかを判断することしかできません。しかし、エラーの有無を判断できれば、エラーが発生していないときの計算結果だけを抽出することで正しい計算結果を知ることができるため、有用なエラー対処法になり得ます。特に、遠隔地の量子コンピュータに通信を介してアクセスするクラウド量子計算ではエラーが未知の場合が多いため、量子計算の検証が威力を発揮します。また、近年では、量子計算の検証を量子エラー抑制に応用するという研究も行われています。以降では、量子計算の検証に関する最近の私たちの成果について紹介します。
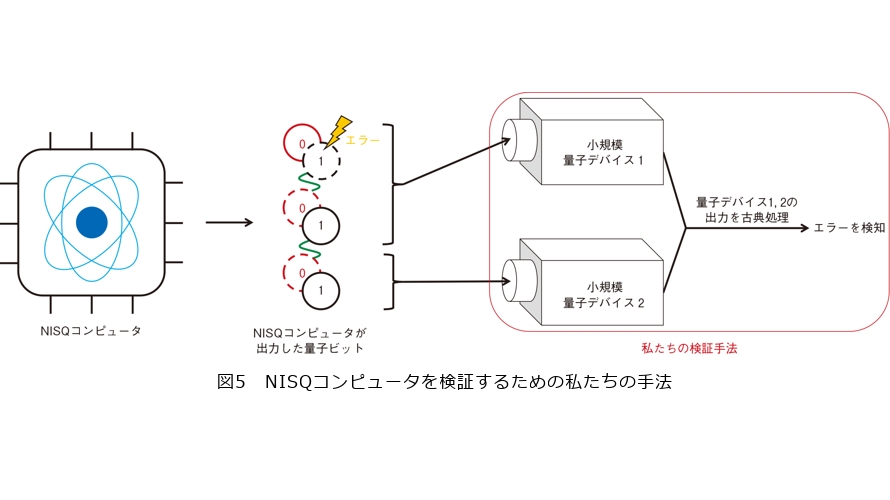
これまで、量子計算の検証を行うためのさまざまなプロトコルが提案されてきましたが、そのほぼすべてがエラー訂正可能な大規模量子コンピュータを想定したものでした。一方で、現在実現している、また今後数年間で実現すると予想されている量子コンピュータはNISQ（Noisy Intermediate-Scale Quantum）コンピュータと呼ばれており、エラー訂正を行う能力がありません。そこで、このギャップを埋めるため、私たちはNISQコンピュータ用の検証手法を構築するという研究に取り組みました^（4）。単純な検証手法では、NISQコンピュータを検証するためには、それと同サイズの別の量子コンピュータが必要になってしまいます。ここでは、量子コンピュータのサイズは扱える量子ビット数を意味しています。この問題を解決するために、私たちは検証用の量子コンピュータを2つの小規模量子デバイスに分割するというアイデアを用いました（図5）。その結果、NISQコンピュータを小規模量子デバイスで効率良く検証する新規な手法を提案することに成功しました。

本稿で紹介した技術は、さまざまなサイズの量子コンピュータに適用できるスケーラブルな技術です。これを可能にしているのは、私たちが得意とする数理科学的アプローチです。今後、量子コンピュータの開発が進むにしたがい、このようなスケーラブルな技術は、ますます重要になってきますが、今なお解明すべき点が多いのが実情です。私たちは、引き続き必要な基礎技術構築に取り組んでいきます。

■参考文献
（1）　谷・高橋：“高速量子アルゴリズムの開発，”電子情報通信学会 基礎・境界ソサイエティ Fundamentals Review，Vol. 14，No. 1，pp. 15-27, 2020.
（2）　A. Hosoyamada, Y. Sasaki, S. Tani, and K. Xagawa:“Quantum algorithm for the multicollision problem,”Theoretical Computer Science, Vol. 842, pp．100-117, 2020.
（3）　S. Akibue, G. Kato, and S. Tani:“Probabilistic unitary synthesis with optimal accuracy,” arXiv:2301.06307，2023.
（4）　Y. Takeuchi, Y. Takahashi, T. Morimae, and S. Tani:“Divide-and-conquer verification method for noisy intermediate-scale quantum computation,”Quantum, Vol. 6, p. 758，2022.