2023年5月号
特集
新たな応用分野を切り拓く量子計算機向けアルゴリズム
- 量子アルゴリズム
- ハッシュ関数
- NP問題
本稿では、量子計算機向けにNTTが考案した新しいアルゴリズムの論文(Verifiable Quantum Advantage without Structure)の概要を解説します。世界中で開発が進む量子計算機は、個別の問題を解くためのアルゴリズムの種類が現状では乏しく、このままでは応用先がごく限られる可能性があります。今回の新アルゴリズムは、この問題の突破口になり得るものです。「構造なしのNP探索問題」と呼ばれる種類の難問の1つを、量子計算機で超高速に回答できることを世界で初めて証明しました。量子計算機の新たな用途の発見につながる成果として、学会でも高く評価されています。
山川 高志(やまかわ たかし)
NTT社会情報研究所
はじめに
次世代の超高速計算機として期待される量子計算機には大きな課題があります。現状のままでは、使い道が狭い範囲に限られることです。
量子計算機の最大の利点は、現在の計算機と比べて超高速の計算が可能なことです。ただし、その恩恵を受けるには、量子計算機の仕組みを活かして効率的に計算するアルゴリズムが不可欠です。ところが、このアルゴリズムが決して豊富とはいえないのです。
実用に堪える量子計算機のハードウェアが登場するには、まだ5〜10年単位の開発期間が必要とみられています。その間に、超高速性を理論で裏打ちできるアルゴリズムをたくさん見つけておかないと、極論すれば宝の持ち腐れになってしまうかもしれません。
今回NTTが考案したアルゴリズムは、この状況を一変させる可能性を秘めています。従来の常識では量子計算機の対象とされていなかった領域の問題を、超高速に解けることを世界で初めて証明したからです(1)。これまで研究者の間では、量子アルゴリズムが対象とする問題には何らかの構造が必要とされてきた*1のに対し、今回のアルゴリズムは構造がない問題を解くことができたのです。
構造がある問題を解く量子アルゴリズムの代表例は、インターネットの標準的な暗号を解ける方法として有名な「Shorのアルゴリズム」(2)でした。Shorのアルゴリズムが発表されたのは1994年なので、今回のアルゴリズムは約30年ぶりに登場した本質的に新しいアイデアといえます。
学会からも高い評価を受けています。成果を記述した論文は、理論計算機科学における最高峰の国際会議「IEEE Symposium on Foundations of Computer Science (FOCS) 2022」に採択されました。Shorのアルゴリズムが発表されたのと同じ会議です。
さらに、量子計算理論の権威の1人、University of Texas at AustinのScott Aaronson教授は、量子力学に関する歴史的な議論で有名なソルべー会議の講演において、本件を最新のブレークスルーとして取り上げました(3)。科学分野の著名なオンライン媒体「Quanta Magazine」によれば、本件に刺激を受けた多くの研究者が、新しい用途の可能性について検討を始めたようです(4)。
*1 後述のAaronson教授らは、量子アルゴリズムによって超高速化を図るには問題に構造が必要との予想を発表しています(3)。なお、この予想の対象が決定問題であるのに対し、NTTの成果は探索問題という違いがあります。
検証可能性も満たす
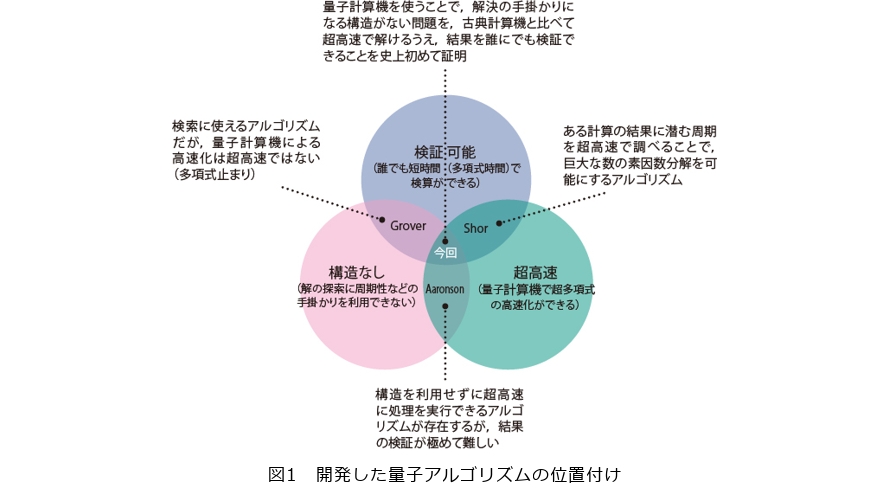
今回の研究成果の位置付けを整理したのが図1です。「超高速」「構造なし」に加えて「検証可能」という性質を同時に満たせることが、開発したアルゴリズムの重要な特徴です。
図が示すように、実は「構造なし」の問題を超高速に解けるアルゴリズムは従来もありました。例えば、前述のAaronson教授が提案した方法です(5)。ただしこれらのアルゴリズムには、検証可能性が欠けていました。
検証可能性とは、アルゴリズムが出した結果が正しいかどうかを簡単に確かめられることです。通常は、量子計算機ではなく従来型の計算機(量子計算機の分野では、古典計算機と呼ばれます)を使って、短時間で検証できることが求められます。ところが、既存のアルゴリズムは検証に極めて長い時間が必要で、出した答えが正解かどうかを事実上確かめられませんでした。これに対して、今回開発したアルゴリズムでは、結果の検証は短時間で済みます。
検証とは具体的にどういうことか、Shorのアルゴリズムを例に説明しましょう。Shorのアルゴリズムは、大きな桁の整数の素因数分解を対象にしています。例えば39,617を分解すると、答えは173×229になります。これが正解であることは、掛け算をすればすぐに確かめられます。数字の桁数が非常に大きくなると、素因数分解自体は古典計算機の手に負えなくなりますが、結果の検証は掛け算だけで済むため、古典計算機でも大して時間がかかりません。
このように検証が容易な(短時間*2で済む)問題は、NP(Non-deterministic Polynomial time)問題と呼ばれます。NTTが今回考案したアルゴリズムの対象もNP問題で、より細かくいえばNP探索問題とされるものです。
*2 ここでの短時間とは、多項式時間(polynomial time)のことを指します。多項式時間とは、問題の大きさ(例えば因数分解する数のビット数)nに対して、答えの計算時間がnの多項式〔nのx乗(xは非負の整数)の項を含む式〕で表せることを意味します。nが大きくなったときの値の増え方が、指数関数(定数のn乗)などと比べて緩やかです。
超多項式の高速性
図1には、構造のない問題を解けて、なおかつ検証可能性も満たす既存方式もあります。「Groverのアルゴリズム」と呼ばれるもので、量子計算機の教科書にも出てくる有名な手法です。この方式には、量子計算機に期待される「超高速性」が足りません。古典計算機のアルゴリズムに対して、せいぜい多項式で表せる高速化しか図れないのです*3。
今回開発したアルゴリズムやShorのアルゴリズムは、指数関数など、多項式を超えた数式で表せる大幅なスピードアップが可能です。例えば、インターネットの標準的な暗号が利用している2048ビットの整数を素因数分解するのは、古典計算機では何万年もかかるとされる難問です。ところが将来の大規模な量子計算機でShorのアルゴリズムを実行すれば、この問題を8時間で解けるという試算があります(6)。
*3 Groverのアルゴリズムは、n個の候補から条件に合うものを選び出す検索問題が対象です。古典アルゴリズムでは平均n/2回、最大n回の問い合わせが必要なのに対し、Groverのアルゴリズムは√n回で済みます。両者を比べると高速化の度合いは二乗程度にとどまります。この程度の高速化では、量子計算機の誤り訂正のオーバヘッドなどで優位性が打ち消される可能性があります(3)。
ランダムな関数の入力を求める
では、Shorのアルゴリズムが利用している構造とは何なのでしょうか。
Shorのアルゴリズムは、ある数Nの素因数分解を、別の問題に置き換えて解いています。まずNと互いに素な自然数xを適当に選び、xのr乗(xr)をNで割ったときの余りを計算します。ここで、rの値を変えていくと、図2(a)にあるように、余りの値は周期的に変化します。この周期が、問題に潜む構造といえます。
実はこの周期を求めることができれば、Nの因数は容易に計算できるのです。古典計算機では周期を求めるために非常に多くの計算が必要なのに対し、Shorのアルゴリズムは量子フーリエ変換という方式を使うことで超高速化を可能にしています。
今回のアルゴリズムが対象とする構造のない問題とは、解決にこのような手掛かりを利用できない問題のことです。量子アルゴリズムの開発では、しばしば処理の中身が分からない関数を対象に、出力から入力を推定する問題を取り上げます。この対象をブラックボックス、またはオラクル(神のお告げ)と呼びます。構造のない問題とは、オラクルの出力に規則性がみられない、すなわち入力に対してランダムな答(ただし同じ入力には同じ答)を返す問題ともいえます。
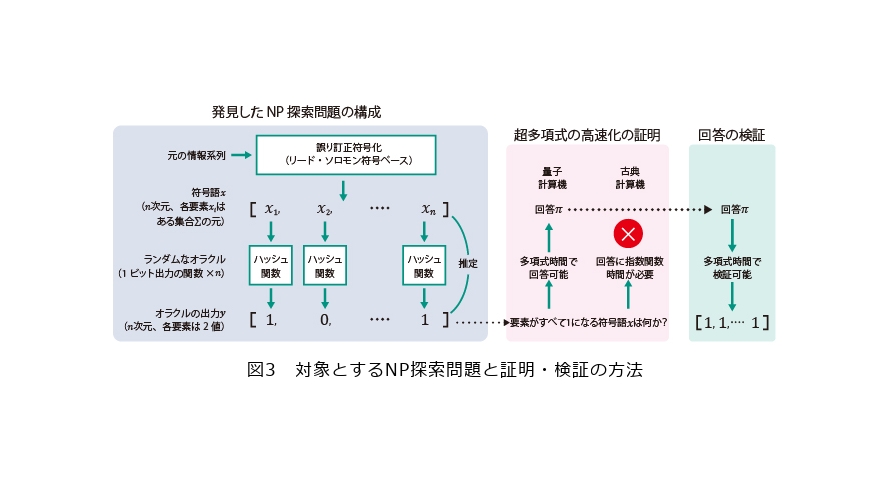
NTTはランダムなオラクルの具体例として、ハッシュ関数*4に注目しました。図2(b)に示すように、ハッシュ関数の入出力の間には規則がみられずランダムといえます。
ただし、ハッシュ関数は量子計算機による攻撃に対して安全なことが知られています。そこでNTTでは、2つの修正を施しました。オラクルへの入力として、ある制約を課したベクトルを利用することと、ベクトルの要素ごとに出力が1ビットのハッシュ関数を適用することです。前者は、入力するベクトルが、別の情報系列を変換した誤り訂正符号*5になっているという条件を加えました(図3)。
この構成で出力から入力を求める問題が、今回のアルゴリズムの対象です。これは構造のないNP探索問題といえます。古典計算機では解決に多大な処理が必要なのに対し、NTTが考案した量子アルゴリズムを使えば、処理量の増大に対して古典計算機と比較して指数関数的に高速に解を求められることを、数学的に示すことができました。そして出した答えの検証は、古典計算機でも簡単に実行できます。つまり、図1に示した3条件をすべて満たせるのです。
*4 ハッシュ関数:入力した数値を別の数値に変換する関数。暗号分野で標準的に利用されるハッシュ関数「SHA-2」などの例があります。
*5 誤り訂正符号:伝えたい情報系列を冗長性のある情報系列に変換して、通信の途中で一部の情報が欠落しても元の情報を再現できるようにする技術。今回はFolded Reed Solomon codeと呼ばれる技術を利用しました。

次の目標は実用化
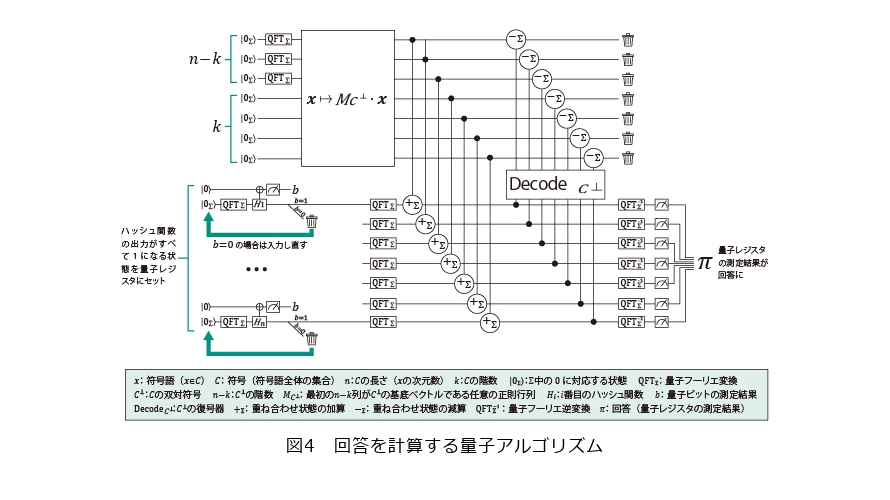
図4が、考案したアルゴリズムを示したものです。量子計算機では、アルゴリズムを量子ゲートと呼ばれる回路の組合せで表すことが普通で、この図もそれにならっています。本稿では詳細を説明できませんが、高速化のポイントの1つが図中の「QFT」で示される量子フーリエ変換にあるとはいえます。ただしShorのアルゴリズムとは異なり、出力の周期のような構造を見つけるために使っているのではありません。
では、このアルゴリズムはどのような用途の役に立つのでしょうか。実は、今回解いた問題はあくまでも量子計算機の可能性を探るためのもので、具体的な応用はありません。本成果が示した新たな方向で、現実的な問題を解くアルゴリズムを探ることは、NTTも含めた世界中の研究機関の大きな課題です。
Shorのアルゴリズムを開発したPeter Shorは、Daniel R. Simonsがある会議に投稿した論文が大きなヒントになったと振り返っています(7)。論文が示したアルゴリズムは非現実的な問題を対象にしたもので、プログラム委員会の一員だったShorの支持にもかかわらず、採択は却下されてしまいました。NTTの論文は幸いにも著名な国際会議で発表できました。論文を読んだ多くの研究者の中から、次なるShorのアルゴリズムが登場することを期待しています。
■参考文献
(1) T. Yamakawa and M. Zhandry:“Verifiable Quantum Advantage without Structure,” Proc. of FOCS 2022, pp. 69-74,Nov. 2022.
(2) S. Aaronson:“How Much Structure Is Needed for Huge Quantum Speedups?,”Sept. 2022.
https://doi.org/10.48550/arXiv.2209.06930
(3) P. W. Shor:“Algorithms for Quantum Computation: Discrete Logarithms and Factoring,”Proc. of FOCS 1994, Nov. 1994.
(4) https://www.quantamagazine.org/quantum-algorithms-conquer-a-new-kind-of-problem-20220711/
(5) S. Aaronson:“BQP and the Polynomial Hierarchy,”Proc.of STOC 2010,Cambridge, U.S.A.,pp. 141-150,June 2010.
(6) C. Gidney and M. Eker˚a:“How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits,”Quantum, Vol. 5, p. 433,April 2021.
(7) P. W. Shor:“The Early Days of Quantum Computation,”Aug. 2022.
https://doi.org/10.48550/arXiv.2208.09964

山川 高志







量子計算はまだ比較的新しい分野で、未解決問題の宝庫です。皆さんもこの分野の研究に取り組んでいただき、ぜひ私たちの提案したアルゴリズムの有用な応用を見つけてください。