2023年8月号
明日のトップランナー
数学理論によるデータ解析で、未知の事象を解明する「C*環・作用素論に基づいた複雑データの解析法」

現在のニューラルネットワークは、大規模データを用いて学習モデルを構築する場合は非常に高精度である一方で、学習に少量のデータしか得られない場合には学習精度が大幅に低下してしまうという課題があります。また現在「事前に異常検知を行う」ICTシステムの運用自動化の分野では、さまざまな状況でのデータ解析を行うために「ノイズがある」「複数データとの相互作用がある・連続的に変化する」など複雑な振る舞いをするデータの解析が求められています。今回はC*環・作用素論といった高度な数学理論をデータ解析に応用して、「少量のデータでもデータ解析の精度の向上」、「ICTシステムの運用自動化」をはじめ、あらゆる社会課題の研究に取り組む橋本悠香特別研究員にお話を聞きました。
橋本悠香
NTTネットワークサービスシステム研究所特別研究員
PROFILE
2018年慶應義塾大学大学院 理工学研究科基礎理工学専攻 修士課程修了。同年、日本電信電話株式会社入社。2022年慶應義塾大学大学院 理工学研究科 基礎理工学専攻博士課程修了。2023年より特別研究員。ネットワーク運用自動化に関する研究に従事。2021年 慶應義塾大学 米沢富美子賞、2018年 慶應義塾大学 藤原賞、2017年情報処理学会情報処理学会 第78回全国大会 大会奨励賞等を受賞。
高度な数学理論をデータ解析に応用し、通信を含めた諸分野の社会課題を解決
■「C*環・作用素論に基づいた複雑データの解析法」とはどのような技術なのでしょうか。
「C*環・作用素論に基づいた複雑データの解析法」とは、行列を一般化した「作用素」という概念を用いて複雑なデータを表現し解析する技術です。この技術が求められている背景として、現在のICTシステムの運用自動化では「ノイズがある」「複数データとの相互作用がある・連続的に変化する」など、複雑な振る舞いをするデータの解析が求められています。例えばネットワークの通信トラフィックでは「A地点の通信量が増加するとB地点の通信量も増加する」といったさまざまな場所での通信トラフィックの相互作用を同時に考えなければなりません。また機器の状態を調べる際には、CPUの使用率やメモリの使用率といった異なるタイプのデータを同時に考える必要があります。そして現状のニューラルネットワークの学習モデルを構築する際には大量のデータが必要ですが、実際には十分なデータが得られず高い精度の学習モデルを構築できない場合があるため、少量のデータでも高精度の分析ができる技術に対する要求が高まっています。
こうした課題に対して従来一般的に用いられていた数学の理論は、実数や複素数といった「1つの値」(スカラ値)の変化を見るというものでした。これに対して「C*環・作用素論に基づいた複雑データの解析法」では、C*環・作用素論などの高度な数学理論を用いてモデルやデータを1つに統合(連続化)し、抽象化して単純化する新しいデータ解析の枠組みを提案します。従来の理論を拡張させた「複数の値を同時に持つような対象を考える」という性質をデータ解析に応用することで、データを解析する際に1種類のデータから複数の値を取り出し、高効率・高精度なデータ解析が可能になります。
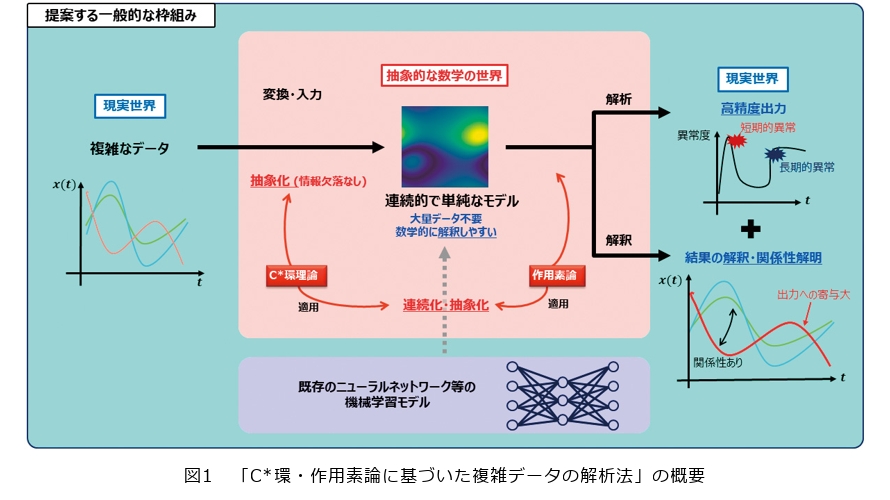
この「C*環・作用素論に基づいた複雑データの解析法」の技術は、複数のデータ間の関係性を解析するために行列やさらにそれを拡張させた数学の概念をうまく利用できないかと漠然と考えていたところ、共同研究者からC*環に関する知識を教えていただき、本格的に適用を始めたことが研究のきっかけです。「C*環・作用素論に基づいた複雑データの解析法」で用いている数学理論は応用分野が限られるものではなく、枠組みとしてはとても一般的なものであるため、通信分野やICTシステムのみならずさまざまな分野に技術展開が可能です。また「光の進み方といった時系列的な変化を連続的な枠組みを使って表すことで、問題を解決することができるのではないか」と検討しています。例えば現在行っている研究では、自然界の動物の脳波や体温などの生体のデータ分析などに本研究を用いています。また高精度に分析したデータを用いることで災害やトラブルなどの事前異常検知を行ったり、通信トラフィック・信号による未知の異常への対応を行ったりすることが可能になります。このように通信の枠組みにとらわれずに機械学習・数学・物理学・生物学・量子力学などで分野横断研究を行い、産業の高度化や自然社会の現象解明など分野を超えた包括的な取り組みをめざしています(図1)。
■具体的な「C*環・作用素論に基づいた複雑データの解析法」の手法について教えてください。
「C*環・作用素論に基づいた複雑データの解析法」では「連続的に時間変化するデータ」を数学の対象とみなして解析を行います。従来では時系列のデータを解析する場合に各時間のデータをバラバラな「点」の集まりとしてとらえていたのに対して、1つの関数という数学的な対象、つまり「線」としてとらえることでより高度なデータ解析が可能になります。
またデータから「固有値」や「特異値」といったデータを特徴付ける値を見つけ出すことで、少ないデータでも高精度な解析を行うことができます。既存の研究ではこの値を見つける際に、データを数学的な情報に変換するために抽象化を行い、離散的に戻して近似的に特徴を抽出していました。しかしこの手法ではデータの性質が失われ解析の精度が低くなってしまうというデメリットがあります。そこで「C*環・作用素論に基づいた複雑データの解析法」では、可能な限り情報が失われるのを防ぎながら連続的にデータを解析する手法に取り組んでいます。ここでの技術的な課題点として、連続的なもの(無限次元)と離散的なもの(有限次元)の性質が全く異なり、それぞれの次元からは考えられないような概念が生まれることが多々起こるという点があります。これによりただ単純に離散的なデータを連続的なデータへ拡張しようと考えてもデータ解析は難しいため、数学の高度な知識を応用し、今ある概念をどう拡張していけばよいのかということを検討しています。データを連続的なまま扱う場合には高度な数学の知識が必要になるため、私自身現在は多くの専門家のお力をいただきながら研究を進めることができています。
■「C*環・作用素論に基づいた複雑データの解析法」のご研究で苦労している点について教えてください。
大きな課題として「現実世界のデータと理論上の数学の世界をいかにして結びつけるか」とういうものがあります。例えばニューラルネットワークの解析では、理論上は数学的に記述しやすい形式の単純な構造としてのニューラルネットワークが検討されています。しかし実際の複雑なニューラルネットワークを完全に再現するためには、データを加工したり情報処理ステップの途中で値をカットしたりなどさまざまな操作が必要であり、現在はそういったところまでは反映しきれていないという状況です。実際にそういった細かい部分の操作を行うことで精度が向上することは実験結果として示されているため、新たに「ニューラルネットワークがどういう仕組みで動いているのか」といった点、そしてそれが解明された場合に「どうすればさらに精度が向上するのか」という点をできるだけ多く検討しながら、現在高精度なニューラルネットワークの構築をめざしています。このようにデータ解析においては理論上単純化して考えるケースが多いため、理論解析や数学理論を用いた手法の構築では現実的な設定を多く取り入れながら解析ができるよう努力していきたいと考えています。
また研究を行う際には理論的な精度を保証するという点に気を付けています。例えばニューラルネットワークでは、学習時に用いたデータモデルがフィットしてデータ分析の精度が高かったとしても、別のデータの場合にはそのデータに対してモデルがフィットせずに精度が低くなってしまうということがあります。これは実際の研究ではもちろん、論文に載っているような結果でも起こり得ることで、論文で「データを使って○○%の精度が達成されました」と書いてあったとしても、実際に自分たちの設定でその技術を使おうとしたときに、同じぐらいの精度の向上が見込まれるかというのは必ずしも保証できません。データが変わると結果が変わってしまうというのはよくあることで、そういった問題が起きないようにするためには、事前にあらゆるデータで高精度のデータ解析を行えるか理論的に調べることに重点を置く必要があります。それによって技術を使う人にも技術をアピールしやすく、安心して運用できることを分かってもらうために重要な取り組みであると考えています。
他分野とコラボレーションを大切に、常に広い視線を持った研究を
■今後の「C*環・作用素論に基づいた複雑データの解析法」の研究ビジョンについて教えてください。
今後の研究ビジョンは、複雑データの解析が求められる通信ネットワークを含めたさまざまな分野に技術を応用し、多くの社会課題を解決していくことです。例えば光は連続的に変化するため「C*環・作用素論に基づいた複雑データの解析法」の枠組みを用いて光の性質を解明することで、NTTが提唱するIOWN(Innovative Optical and Wireless Network)構想に貢献することが可能になると考えています。
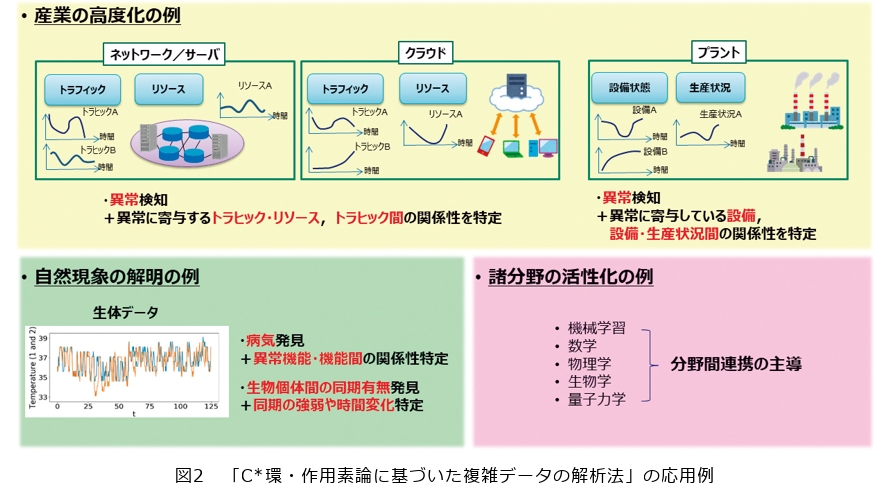
また今後新たに取り組む研究ビジョンとして、生物学で解析されている問題と通信ネットワークのデータ解析には似た特徴があるため、生物の専門家と連携・協力して動物の睡眠といった動物の性質に関する解明を考えています。このように「C*環・作用素論に基づいた複雑データの解析法」で用いられている数学の枠組みはとても一般的な設定であるため、今後もさまざまな分野の方とコラボレーションの幅を広げていきたいと考えています。さまざまな分野の課題に技術を応用することで、これまでバラバラに調べられていたものを1つにまとめて考え、産業界・自然界のさまざまな問題の解決に貢献することをめざします(図2)。
■最後に研究者・学生・ビジネスパートナーの方々へ向けてメッセージをお願いします。
私は「C*環・作用素論に基づいた複雑データの解析法」の研究を進める中で、数学の「応用」と「理論」の橋渡しをする役目を担っています。そのためさまざまな方々と一緒に研究を行う機会が多く、またそれを社内で共有するという場面も多々あります。こうした状況において、例えば少人数のグループの中で行っている研究を他のグループに共有して「こういうところにも技術が使えるのではないか」というように、自分が今まで考えついていなかった応用のアイデアをもらえることは研究においてとても有益な活動であり、研究の喜びを感じる瞬間でもあります。そのため多くの方と交流をしながら研究を進めることを大事にしています。
NTTは基礎研究から実用化まで幅広く研究しており、私が所属しているNTTネットワークサービスシステム研究所は「応用」と「理論」の両方に取り組んでいるため、その点でとても魅力的な環境です。例えば実際に開発に携わっている周りの方と話をして目標感や実際の課題についてすぐに知ることができたり、学術的な観点からのコメントをもらうことができたりすることなどにより、研究が円滑に進められています。例えば私が所属している部署ではICTシステムの運用自動化にかかわる要素技術を研究開発していますが、多様な知識とバックグラウンドを持った同僚がおり、日々刺激を受けながら研究をしています。
もちろん1つの分野に特化するということは研究者にとって大切であり、ないがしろにしてはいけないと思います。しかし一方で、それだけにこだわりすぎると見えてこないことが多くあります。研究においてはやはり広い視点を持つということは重要で、私自身なるべく1つの分野にとどまらずに活動することを意識しています。確かに近い分野の方と共同研究を行う環境は、周囲の理解は得やすく話が通じやすいため楽に研究を進めることができます。しかしそこから1歩飛び出して、例えば他分野の方の話を聞いたり普段とは違う分野の学会に参加したりすることで、今までになかった新しい視点を得ることができるはずです。私自身も今までとは異なる他分野の方と協力してみることで自分の考えの間違いに気が付き、違う分野の方と話したときに全く話が通じず「自分はすごく狭いところでしか考えていなかったんだ」というような新たな気付きを得ることができて、研究者としてとても大きなプラスになったと感じています。
1人で新しい領域に踏み出すことはとても大変ですが、踏み出した先にはきっと今までに見たことのない面白い世界が待っていると思います。私自身もこれからさらに視野を広げていきたいと考えていますし、これを読んでいる皆さんにも、ぜひ自分と違う分野の方と話をしてみるところから、新しい扉を開くことを始めてほしいなと願っています。





