2024年7月号
特集
対称性とリー群・リー環の表現論
- 基礎数学
- リー群
- リー環
リー群の表現とは、線形空間の連続的な対称性を抽象化したものです。また、その微分(線形近似)を考えることにより、リー環の表現を得ることができます。これらはフーリエ解析の一般化とみなすことができ、さらに数学のみならず物理学等においても重要な道具となっています。本稿では、リー群・リー環の表現の基本的かつ重要な具体例についていくつか紹介します。また、筆者自身の最新の研究についても簡単に触れます。
中濱 良祐(なかはま りょうすけ)
NTT基礎数学研究センタ
はじめに
リー群は、空間の連続的な対称性を抽象化したものです。特に、線形な対称性を考えたものはリー群の表現と呼ばれます(1)。リー群の表現は、例えば対称性を持った空間上の関数を解析する際などに役立ちます。ただ、リー群そのものは非線形な対象のため、その表現をそのまま扱うのは容易ではありません。そこで、代わりにこの微分(線形近似)を考えることにより、リー環の表現を考えることが有用です。これは元のリー群の表現の情報をほとんど保持しており、より扱いやすい対象となっています。
リー群の表現とは
まず、リー群は複素数を成分とする可逆な ![]() ×
× ![]() 行列の全体〔これを通常
行列の全体〔これを通常 ![]() (
( ![]() ,
, ![]() )などと表し、一般線形群(general linear group)と呼びます〕の部分集合であって、積と逆行列、および極限を取る操作で閉じたものを指します*1。例えば、
)などと表し、一般線形群(general linear group)と呼びます〕の部分集合であって、積と逆行列、および極限を取る操作で閉じたものを指します*1。例えば、 ![]() (
( ![]() ,
, ![]() ) そのものや、
) そのものや、
![]() {実数を成分とする可逆な
{実数を成分とする可逆な ![]() ×
× ![]() 行列}、
行列}、
![]() 、
、
![]() 、
、
![]()
などがリー群の典型的な例となります(ここで ![]() は単位行列を表します)。次に
は単位行列を表します)。次に ![]() をリー群、
をリー群、 ![]() を“極限が定義できる”空間〔これを位相空間(topological space)と呼びます〕とします。
を“極限が定義できる”空間〔これを位相空間(topological space)と呼びます〕とします。![]() の元
の元 ![]() を1つ取るごとに
を1つ取るごとに ![]() 上の変換
上の変換 ![]() (
( ![]() ):
): ![]() →
→ ![]() が定まり、適当な意味での結合法則と連続性を満たすとき、リー群
が定まり、適当な意味での結合法則と連続性を満たすとき、リー群 ![]() は空間
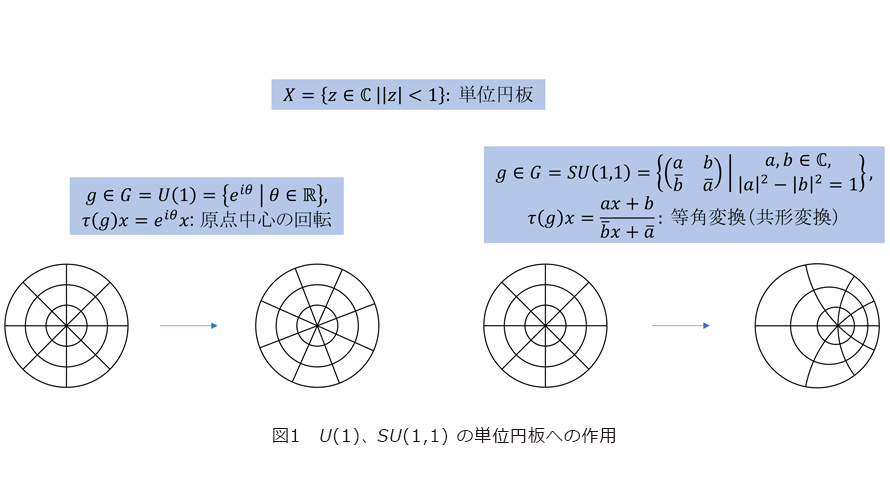
は空間 ![]() に作用するといいます。例えば、単位円板(半径1の円)の原点を中心とする回転の全体は、リー群
に作用するといいます。例えば、単位円板(半径1の円)の原点を中心とする回転の全体は、リー群 ![]() (1) の作用とみなすことができ、また単位円板の等角変換(共形変換)、すなわち交わる二曲線の角度を保つ変換の全体は、ほぼリー群
(1) の作用とみなすことができ、また単位円板の等角変換(共形変換)、すなわち交わる二曲線の角度を保つ変換の全体は、ほぼリー群 ![]() ( 1,1 )の作用とみなすことができます(図1)。このようにリー群
( 1,1 )の作用とみなすことができます(図1)。このようにリー群 ![]() が空間
が空間 ![]() に作用するとき、
に作用するとき、![]() の対称性が
の対称性が ![]() によって記述されるとみなせます。さらに作用を受ける空間
によって記述されるとみなせます。さらに作用を受ける空間 ![]() =
= ![]() が線形空間で
が線形空間で ![]() (
( ![]() ) が
) が ![]() 上の線形写像(すなわち和とスカラー倍を保つ写像)のとき、(
上の線形写像(すなわち和とスカラー倍を保つ写像)のとき、( ![]() ,
, ![]() )は
)は ![]() の表現(representation)と呼ばれます。例えば
の表現(representation)と呼ばれます。例えば ![]() が空間
が空間 ![]() に作用するとき、
に作用するとき、![]() はその上の関数空間(例えば
はその上の関数空間(例えば ![]() 二乗可積分空間など)にも自動的に作用します。この作用は線形となり、よって
二乗可積分空間など)にも自動的に作用します。この作用は線形となり、よって ![]() は
は ![]() の表現となります。これは一般には無限次元の一見難しい表現となりますが、多くの場合複数のより簡単な表現を束ねたものになっています。したがって関数空間の理解には、より簡単な表現を詳しく理解することが重要となります。リー群
の表現となります。これは一般には無限次元の一見難しい表現となりますが、多くの場合複数のより簡単な表現を束ねたものになっています。したがって関数空間の理解には、より簡単な表現を詳しく理解することが重要となります。リー群![]() ⊂
⊂ ![]() (
( ![]() ,
, ![]() )の表現の例としてもっとも単純なものは、
)の表現の例としてもっとも単純なものは、![]() (縦ベクトルの空間)として、各
(縦ベクトルの空間)として、各 ![]() ∈
∈ ![]() に対し、
に対し、 ![]() (
( ![]() )を
)を
![]()
と単に行列の積で定めるものです。より非自明な例として、![]() を非負整数としたとき、リー群
を非負整数としたとき、リー群 ![]() =
= ![]() (
( ![]() ) の、線形空間
) の、線形空間 ![]() =
= ![]() (式(1)、
(式(1)、 ![]() 変数
変数 ![]() 次斉次多項式の空間)への作用
次斉次多項式の空間)への作用 ![]() (
( ![]() ) を変数への行列の積によって定めたものや、リー群
) を変数への行列の積によって定めたものや、リー群 ![]() =
= ![]() (
( ![]() ) の、線形空間
) の、線形空間 ![]() =
= ![]() (式(2)、
(式(2)、![]() 変数
変数 ![]() 次斉次調和多項式の空間)への作用
次斉次調和多項式の空間)への作用 ![]() (
( ![]() ) を同様に定めたものも表現となります。特に
) を同様に定めたものも表現となります。特に ![]() (
( ![]() ) の
) の ![]() 上の表現、
上の表現、![]() (
( ![]() ) の
) の ![]() 上の表現は、既約表現(それ以上分解できない表現、すなわち
上の表現は、既約表現(それ以上分解できない表現、すなわち ![]() (
( ![]() )
) ![]() ⊂
⊂ ![]() を満たす線形部分空間
を満たす線形部分空間 ![]() ⊂
⊂ ![]() が{0}と
が{0}と ![]() 自身以外に存在しない表現)の例になっています。
自身以外に存在しない表現)の例になっています。
*1 より一般に、リー群は群構造と多様体構造を持ち、かつ群演算が微分可能なものを指します。特に、行列の閉部分群としては実現できませんが、これと局所的に同型なものもリー群に含まれます。

表現の既約分解──フーリエ解析の一般化
表現論における基本的な問題の1つは、与えられた表現を既約表現の和に分解することです。特にリー群 ![]() が作用する空間
が作用する空間 ![]() 上の関数空間(
上の関数空間( ![]() など)の既約分解は、この空間
など)の既約分解は、この空間 ![]() を理解するうえで役立ちます。例えば
を理解するうえで役立ちます。例えば ![]() =
= ![]() (
( ![]() )は
)は ![]() − 1 次元球面
− 1 次元球面 ![]()
![]() に通常の回転として作用し、さらにその上の関数空間
に通常の回転として作用し、さらにその上の関数空間 ![]() にも線形に作用します。このとき、
にも線形に作用します。このとき、![]() 次斉次調和多項式を球面
次斉次調和多項式を球面 ![]() に制限した関数(球面調和関数(2))からなる空間(これを
に制限した関数(球面調和関数(2))からなる空間(これを ![]() で表します)はこの作用で保たれ、部分表現となります。すなわち、
で表します)はこの作用で保たれ、部分表現となります。すなわち、![]() ならば、任意の
ならば、任意の ![]() ∈
∈ ![]() (
( ![]() ) に対し、
) に対し、![]() 。さらに、任意の
。さらに、任意の ![]() は
は
![]()
の形に一意的に表すことができます。したがって、![]() は
は
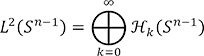
と直和分解されます。いま、各 ![]() は既約なので、これが既約分解となります。特に
は既約なので、これが既約分解となります。特に ![]() = 2 の場合には、
= 2 の場合には、![]() の座標を(cos
の座標を(cos ![]() , sin
, sin ![]() )で表すと、
)で表すと、![]() は式(3)と表すことができ、上記の分解はフーリエ級数展開(式(4))に一致します。同様に、フーリエ(逆)変換
は式(3)と表すことができ、上記の分解はフーリエ級数展開(式(4))に一致します。同様に、フーリエ(逆)変換
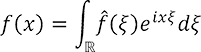
は、実数の集合 ![]() 上の関数空間
上の関数空間 ![]() (
( ![]() ) を加法群
) を加法群 ![]() の表現として、一次元部分表現
の表現として、一次元部分表現 ![]() の和で表したもの
の和で表したもの
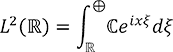
とみなすことができます。ただし、この場合非可算個の空間の和なので、直和分解ではなく直積分分解と呼ばれます。いうまでもなくフーリエ解析は信号処理をはじめ多くの分野で重要であり、また球面調和関数も量子力学で回転対称な系を扱う場合などに重要です。一般の表現の既約分解もこれらの重要な理論の一般化とみなせます。
既約分解の中でも特に、リー群 ![]() の表現をその部分群
の表現をその部分群 ![]() ′⊂
′⊂ ![]() の表現とみなして分解する場合を分岐則(branching law)と呼びます。例えば、
の表現とみなして分解する場合を分岐則(branching law)と呼びます。例えば、![]() =
= ![]() (
( ![]() ) の部分群
) の部分群 ![]() ′ ≃
′ ≃ ![]() (
( ![]() − 1 )(式(5))を考え、
− 1 )(式(5))を考え、![]() (
( ![]() )の表現
)の表現 ![]() を部分群
を部分群 ![]() ′ ≃
′ ≃ ![]() (
( ![]() − 1 ) に制限することを考えましょう。このとき、
− 1 ) に制限することを考えましょう。このとき、![]() は
は ![]() (
( ![]() ) の表現としては既約ですが、
) の表現としては既約ですが、![]() (
( ![]() − 1 )の表現としてみると、
− 1 )の表現としてみると、![]() (式(6),
(式(6), ![]() = 0, … .
= 0, … . ![]() ) は明らかに部分表現となります。したがって
) は明らかに部分表現となります。したがって ![]() の
の ![]() (
( ![]() − 1) のもとでの既約分解(分岐則)は式(7)で与えられることが分かります。同様に、
− 1) のもとでの既約分解(分岐則)は式(7)で与えられることが分かります。同様に、![]() の
の ![]() ′ =
′ = ![]() (
( ![]() ) のもとでの既約分解は式(8)(ただし
) のもとでの既約分解は式(8)(ただし ![]() )で与えられることが知られています。より非自明な例として、
)で与えられることが知られています。より非自明な例として、![]() =
= ![]() (
( ![]() ) の表現
) の表現 ![]() の部分群
の部分群 ![]() ′≃
′≃ ![]() (
( ![]() − 1 ) のもとでの分岐則を考えてみましょう。今、
− 1 ) のもとでの分岐則を考えてみましょう。今、![]() = 0 , 1 , ... ,
= 0 , 1 , ... , ![]() に対し、
に対し、![]() を
を ![]() −
− ![]() 次以下の多項式で
次以下の多項式で ![]() を満たすとして、線形空間
を満たすとして、線形空間 ![]() (式(9))を考えると、これは
(式(9))を考えると、これは ![]() (
( ![]() − 1 ) の既約表現であり、さらに多項式
− 1 ) の既約表現であり、さらに多項式 ![]() をうまく選ぶと、
をうまく選ぶと、![]() ⊂
⊂ ![]() とすることができます。このとき、
とすることができます。このとき、![]() は
は ![]() (
( ![]() − 1 ) のもとで、式(10)のように既約分解されます。この
− 1 ) のもとで、式(10)のように既約分解されます。この ![]() は、実際にラプラシアンから導かれる微分方程式を解くことで求まり、ゲーゲンバウアー多項式
は、実際にラプラシアンから導かれる微分方程式を解くことで求まり、ゲーゲンバウアー多項式 ![]() を用いて
を用いて ![]() となることが分かります。
となることが分かります。 ![]() = 3 の場合にはこれはルジャンドル陪多項式の定数倍で与えられます。これを使うと、
= 3 の場合にはこれはルジャンドル陪多項式の定数倍で与えられます。これを使うと、![]() の基底を小さい
の基底を小さい ![]() から順番に具体的に構成することができます(図2:
から順番に具体的に構成することができます(図2: ![]() = 3の場合)。
= 3の場合)。
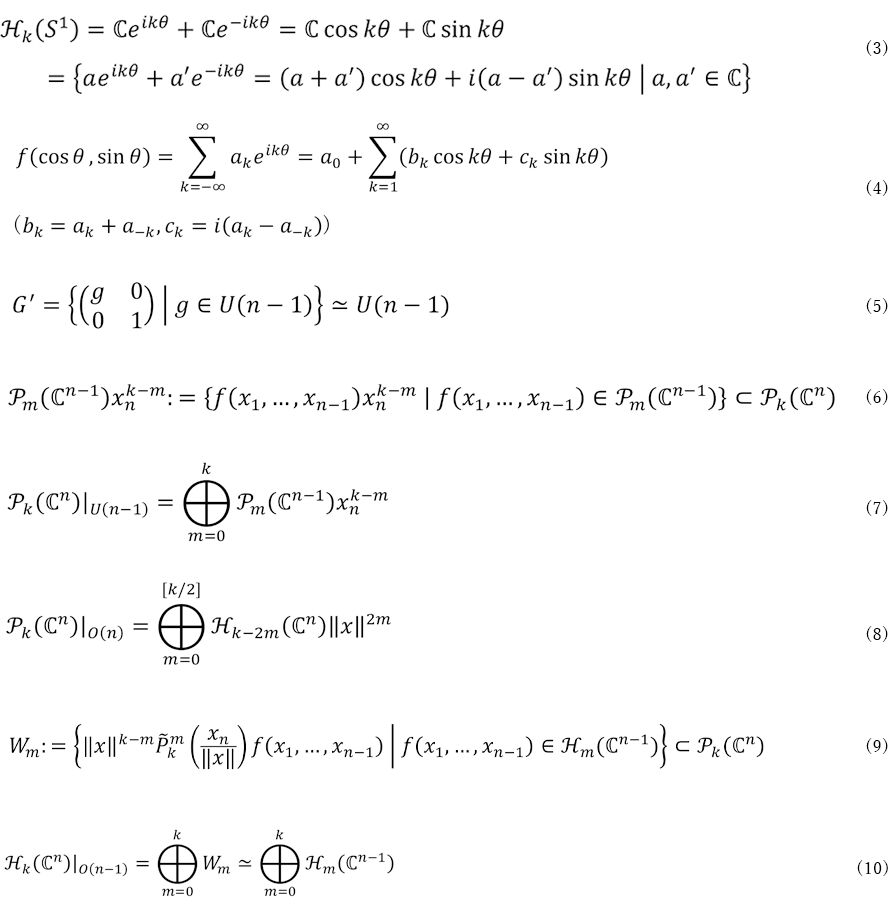
リー環の表現──リー群の表現の線形近似
さて、一般にリー群は線形空間ではないため、その表現をそのまま扱うのは容易ではありません。そこでリー群の代わりに、これに付随するリー環を考えます。今、![]() ∈
∈ ![]() (
( ![]() ,
, ![]() )(複素数を成分とする
)(複素数を成分とする ![]() ×
× ![]() 行列)、
行列)、![]() ∈
∈ ![]() として、指数関数
として、指数関数 ![]() を考えると、これは通常の指数法則
を考えると、これは通常の指数法則 ![]() と、
と、![]() を満たします。そこで、リー群
を満たします。そこで、リー群 ![]() ⊂
⊂ ![]() (
( ![]() ,
, ![]() ) に対し、付随するリー環
) に対し、付随するリー環 ![]() (
( ![]() ) ⊂
) ⊂ ![]() (
( ![]() ,
, ![]() )を
)を
![]()
で定義します。するとこれは線形空間となり、さらに ![]() ,
,![]() ∈
∈ ![]() (
( ![]() ) に対し、[
) に対し、[ ![]() ,
, ![]() ]: =
]: = ![]()
![]() −
− ![]()
![]() ∈
∈ ![]() (
( ![]() ) となることが知られています。次に、(
) となることが知られています。次に、( ![]() ,
, ![]() ) をリー群
) をリー群 ![]() の有限次元表現としたとき、付随するリー環
の有限次元表現としたとき、付随するリー環 ![]() (
( ![]() ) の表現 (
) の表現 ( ![]()
![]() ,
, ![]() ) を式(11)により定めると、
) を式(11)により定めると、![]() 、
、![]() ∈
∈ ![]() (
( ![]() ) 、
) 、![]() 、
、 ![]() ∈
∈ ![]() に対し、
に対し、![]()
![]() (
( ![]()
![]() +
+ ![]()
![]() ) =
) = ![]()
![]()
![]() (
( ![]() ) +
) + ![]()
![]()
![]() (
( ![]() )かつ
)かつ![]()
![]() ([
([ ![]() ,
, ![]() ]) =
]) = ![]()
![]() (
( ![]() )
) ![]()
![]() (
( ![]() ) −
) − ![]()
![]() (
( ![]() )
) ![]()
![]() (
( ![]() ) が成立します。このようにつくった表現 (
) が成立します。このようにつくった表現 ( ![]()
![]() ,
, ![]() ) は元の表現 (
) は元の表現 ( ![]() ,
, ![]() ) の情報をほとんど保持しています。例えば、もし
) の情報をほとんど保持しています。例えば、もし ![]() が連結ならば、有限次元表現(
が連結ならば、有限次元表現( ![]() ,
, ![]() ) が
) が ![]() の表現として既約であることと、その微分表現 (
の表現として既約であることと、その微分表現 ( ![]()
![]() ,
, ![]() ) が
) が ![]() (
( ![]() ) の表現として既約であることは同値になります。
) の表現として既約であることは同値になります。
例として、![]() =
= ![]() (2): =
(2): = ![]() (2) ∩ ( 2 ,
(2) ∩ ( 2 , ![]() ) の
) の![]() =
= ![]() への表現を考えましょう。今、
への表現を考えましょう。今、![]() =
= ![]() (2)に付随するリー環
(2)に付随するリー環 ![]() (
( ![]() ) =
) = ![]() (2) およびその複素化
(2) およびその複素化 ![]() (
( ![]() ) ⊗
) ⊗ ![]() =
= ![]() ( 2,
( 2, ![]() ) は式(12)で与えられます。
) は式(12)で与えられます。![]() ( 2,
( 2, ![]() ) の基底として
) の基底として ![]() 、
、![]() 、
、![]()
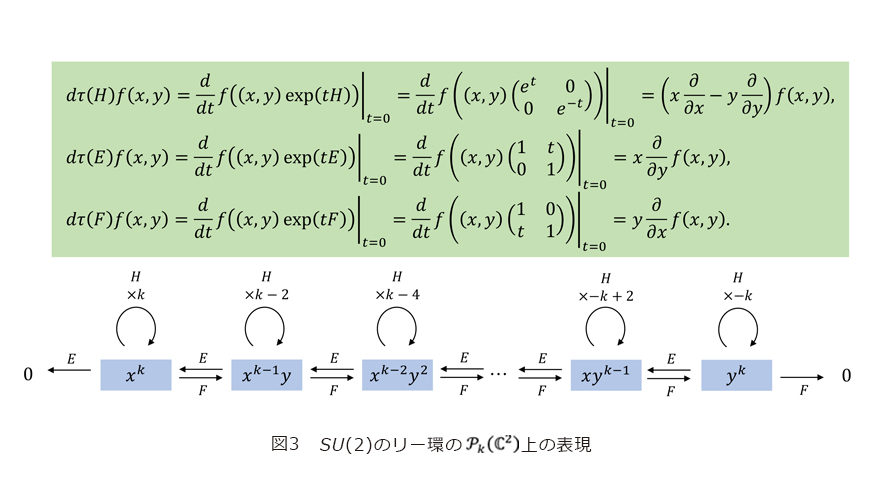
を取ると、これらの ![]() への作用は式(13)となります(途中式を図3に示します)。特に
への作用は式(13)となります(途中式を図3に示します)。特に ![]() の基底として
の基底として ![]() を取ったとき、これらの作用は式(14)となります。したがって
を取ったとき、これらの作用は式(14)となります。したがって ![]()
![]() (
( ![]() ) の固有値の全体は {
) の固有値の全体は { ![]() .
. ![]() − 2 ,
− 2 , ![]() − 4 , … , −
− 4 , … , −![]() } となり、
} となり、 ![]()
![]() (
( ![]() ) は
) は ![]()
![]() (
( ![]() ) の固有ベクトルの固有値を2上げ、逆に
) の固有ベクトルの固有値を2上げ、逆に ![]()
![]() (
( ![]() ) は固有値を2下げることが分かります。これは量子力学におけるスピン表現と同値なものです。実は一般に
) は固有値を2下げることが分かります。これは量子力学におけるスピン表現と同値なものです。実は一般に ![]() ( 2 ) の既約表現は必ずこのような構造を持ち、特にある非負整数
( 2 ) の既約表現は必ずこのような構造を持ち、特にある非負整数 ![]() について
について ![]() と同値になることが示せます。より難しい例として、リー群
と同値になることが示せます。より難しい例として、リー群 ![]() (
( ![]() ) の表現を考えた場合にも、付随するリー環(の複素化)の作用を対角行列、上三角行列、下三角行列のそれぞれについて詳しくみることにより、
) の表現を考えた場合にも、付随するリー環(の複素化)の作用を対角行列、上三角行列、下三角行列のそれぞれについて詳しくみることにより、 ![]() (
( ![]() ) の既約表現の全体が、単調減少な
) の既約表現の全体が、単調減少な ![]() 個の整数の組(式(15))と一対一に対応することが示せます。このようにリー環の表現はリー群の表現を分類するうえで役立ちます。さらに
個の整数の組(式(15))と一対一に対応することが示せます。このようにリー環の表現はリー群の表現を分類するうえで役立ちます。さらに ![]() (
( ![]() ) の各既約表現の次元は、半標準ヤング盤(semistandard Young tableaux)と呼ばれる組合せ論的対象の個数で特徴付けられることも知られています。
) の各既約表現の次元は、半標準ヤング盤(semistandard Young tableaux)と呼ばれる組合せ論的対象の個数で特徴付けられることも知られています。
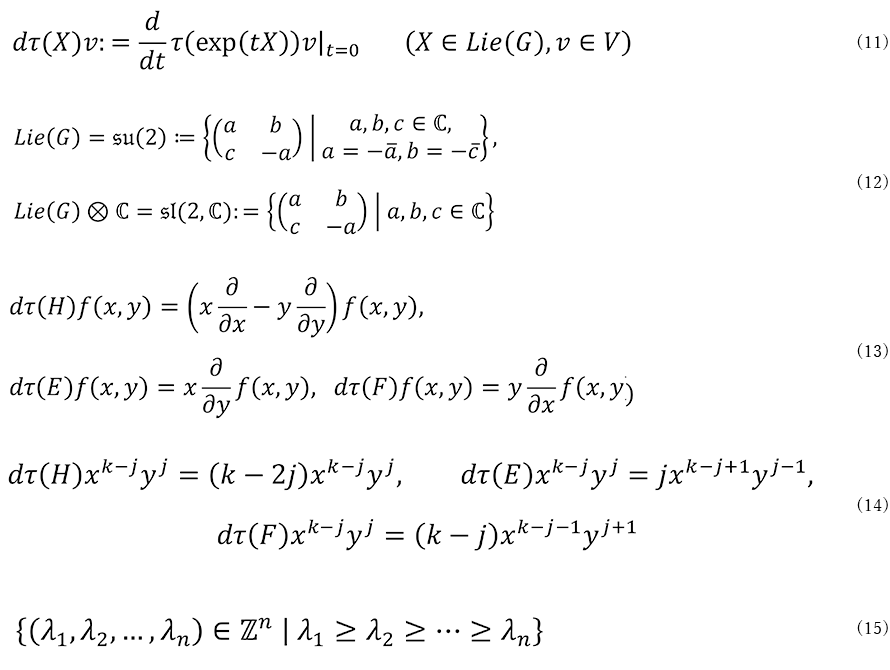
無限次元表現の例
ここまでは有限次元表現を中心にみてきましたが、無限次元表現の例についてもみてみましょう。今リー群 ![]() =
= ![]() ( 2 ,
( 2 , ![]() ) を考えると、付随するリー環
) を考えると、付随するリー環 ![]() (
( ![]() ) =
) = ![]() ( 2 ,
( 2 ,![]() ) は式(16)で与えられます。
) は式(16)で与えられます。![]() ,
, ![]() ,
, ![]() ∈
∈ ![]() ( 2 ,
( 2 , ![]() ) を前述のものと同様に取り、
) を前述のものと同様に取り、![]() =
= ![]() (
( ![]() )(のある稠密部分空間)への
)(のある稠密部分空間)への ![]() ( 2 ,
( 2 , ![]() ) の作用
) の作用 ![]()
![]() を式(17)で定めます。すると、これはリー群
を式(17)で定めます。すると、これはリー群 ![]() ( 2,
( 2, ![]() ) の表現には持ち上がりませんが、その二重被覆群
) の表現には持ち上がりませんが、その二重被覆群 ![]() には持ち上がる〔すなわち、
には持ち上がる〔すなわち、![]() の表現 (
の表現 ( ![]() ,
, ![]() (
( ![]() ) ) で、その微分が(ある稠密部分空間上で)上述の
) ) で、その微分が(ある稠密部分空間上で)上述の ![]()
![]() に一致するものがある〕ことが知られています。さらに
に一致するものがある〕ことが知られています。さらに ![]() の作用がフーリエ変換の定数倍に一致します(式(18))。これは
の作用がフーリエ変換の定数倍に一致します(式(18))。これは ![]() (量子調和振動子)の固有関数を考察することで示せます。この表現 (
(量子調和振動子)の固有関数を考察することで示せます。この表現 ( ![]() ,
, ![]() (
( ![]() ) は無限次元ながら既約に近い表現*2であり、ヴェイユ表現、メタプレクティック表現などと呼ばれます。この構成はより大きなリー群
) は無限次元ながら既約に近い表現*2であり、ヴェイユ表現、メタプレクティック表現などと呼ばれます。この構成はより大きなリー群 ![]() (
( ![]() ,
, ![]() ) の表現
) の表現 ![]() に一般化されます(
に一般化されます( ![]() = 1 の場合
= 1 の場合 ![]() ( 1.
( 1. ![]() ) =
) = ![]() ( 2 ,
( 2 , ![]() ))。さらに
))。さらに ![]() (
( ![]()
![]() ,
, ![]() ) の表現
) の表現 ![]() (
( ![]() ×
× ![]() 行列上の関数空間)を部分群
行列上の関数空間)を部分群 ![]() (
( ![]() ,
, ![]() ) ×
) × ![]() (
( ![]() ) ⊂
) ⊂ ![]() (
( ![]()
![]() ,
, ![]() ) のもとで既約分解することにより、
) のもとで既約分解することにより、 ![]() (
( ![]() ,
, ![]() ) の多彩な表現を得ることができるなど、ヴェイユ表現は表現論の中でも特に重要視されています。
) の多彩な表現を得ることができるなど、ヴェイユ表現は表現論の中でも特に重要視されています。
*2 偶関数、奇関数の全体がそれぞれ既約表現であり、 ![]() (
( ![]() ) は2つの既約表現の和になります。
) は2つの既約表現の和になります。
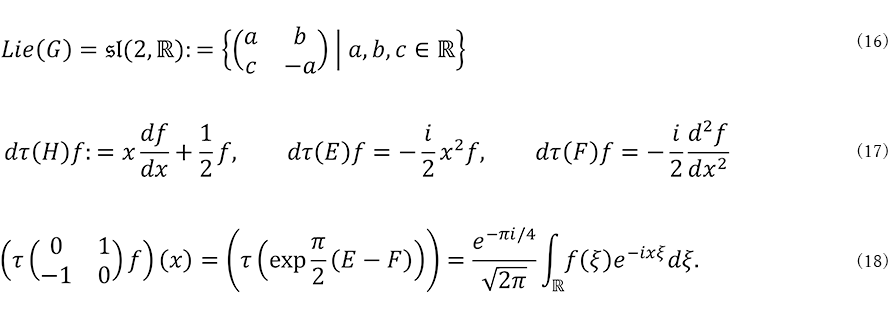
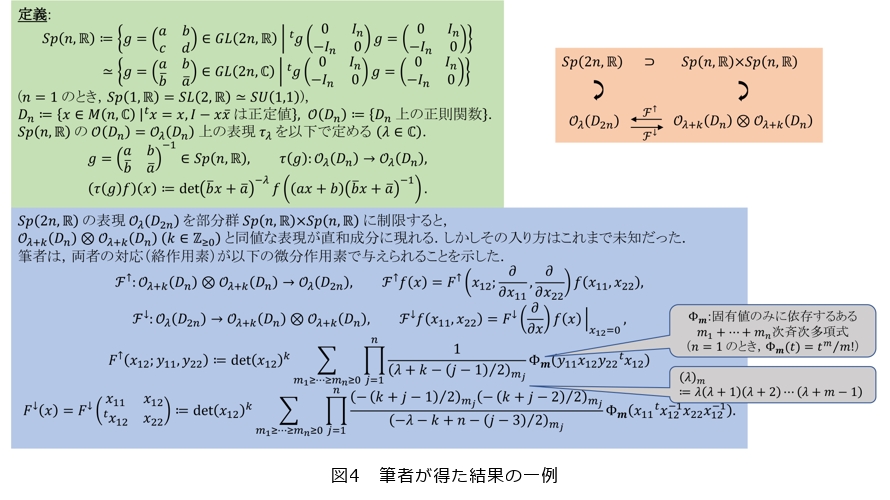
無限次元表現の分岐則
筆者は現在の研究として、無限次元表現の分岐則を具体的に記述することに関心を持っています(3)。リー群 ![]() の“良い”無限次元表現 (
の“良い”無限次元表現 ( ![]() ,
, ![]() ) を部分群
) を部分群 ![]() ′ ⊂
′ ⊂ ![]() に制限すると、
に制限すると、![]() は
は ![]() ′ の(一般には無限個の)既約表現の直和(または直積分)に分解されます。このとき、抽象的に
′ の(一般には無限個の)既約表現の直和(または直積分)に分解されます。このとき、抽象的に ![]() ′ のどの表現
′ のどの表現 ![]() ′ が分解に現れるかが分かったとしても、その具体的な入り方まで決定するのは一般には難しい問題です(
′ が分解に現れるかが分かったとしても、その具体的な入り方まで決定するのは一般には難しい問題です( ![]() の例における
の例における ![]() の決定に相当)。筆者は素性の良い (
の決定に相当)。筆者は素性の良い ( ![]() ,
, ![]() ′,
′, ![]() ,
, ![]() ′ ) に対して、
′ ) に対して、![]() ′ の
′ の ![]() への入り方(絡作用素、intertwining operator)を具体的に決定しました(4)(5)(図4)。そこには超幾何関数をはじめとする特殊関数(の多変数化)が現れます。今後はより一般の (
への入り方(絡作用素、intertwining operator)を具体的に決定しました(4)(5)(図4)。そこには超幾何関数をはじめとする特殊関数(の多変数化)が現れます。今後はより一般の ( ![]() ,
, ![]() ′,
′, ![]() ,
, ![]() ′ ) に対して同様の結果を得ることを目標としています。
′ ) に対して同様の結果を得ることを目標としています。
■参考文献
(1) 小林・大島:“リー群と表現論,”岩波書店,2005.
(2) 野村:“球面調和函数と群の表現,”日本評論社,2018.
(3) T. Kobayashi:“A program for branching problems in the representation theory of real reductive groups,”Representations of reductive groups, Progr. Math., Vol. 312, pp. 277-322, Birkhäuser/Springer, Cham, 2015.
(4) R. Nakahama:“Construction of intertwining operators between holomorphic discrete series representations,”SIGMA Vol. 15, No. 36, p. 101, 2019.
(5) R. Nakahama:“Computation of weighted Bergman inner products on bounded symmetric domains and restriction to subgroups,” SIGMA Vol. 18, No. 33, p. 105, 2022.

中濱 良祐







本稿では長さの制約もあり、リー群の表現論のごく一部にしか触れませんでしたが、この分野にはほかにも多くの魅力的な話題があります。拙文ではありますが、少しでもこの分野が面白いと思っていただけたら幸いです。