2024年7月号
特集
光と物質の相互作用とゼータ関数
- 量子ラビ模型
- 非可換調和振動子
- 分配関数
量子系における分配関数と対応するスペクトルのゼータ関数を知ることの重要性は、物理と数学のそれぞれにおいて等しいものです。本稿では、光と物質の相互作用の背後に隠れる整数論的な構造を、多様な数学を基盤に相互作用の分配関数とスペクトルゼータ関数の特殊値に着目して考察します。
Cid Reyes-Bustos
若山 正人(わかやま まさと)
NTT基礎数学研究センタ
はじめに
数えることが人類の数学の始まりです。ピタゴラス学派による発見だと推測されますが、文献上はユークリッド原論にあるとおり、2500年前ごろには ①構成的方法による素数の無限性と ②自然数は一意的に素因数分解できることが証明されていました。数論への興味は、ある意味で、整数の単純さ(そう見えること)と、その構成要素である素数の不規則・複雑にみえる構造とのギャップにあります。提示以来165年間未解決なリーマン予想が持つ魅力もここにあります。一方で、 光と物質の相互作用を制御することは量子情報における要です。本稿では、そのもっとも基本的な理論モデルである量子ラビ模型(1)に着目します。知りたいことはその時間発展です。中でも系の分配関数を知ることが重要です。ところで分配関数のココロは、気体粒子や電子のような個々にはバラバラな状態を持つ(ミクロな)粒子が集まったときの(マクロな)性質を理解したい点にあります。具体的には粒子のとり得るエネルギーに関して重みをつけて足し合わせたものとして分配関数は定義されます。実はリーマンのゼータ関数も、バラバラに存在しているようにみえる各素数のそれぞれが定める幾何級数を素数全体にわたり積(下述のオイラー積)をとったものです。ゼータ関数を精密に観察することによって個々の素数だけを見ていては決して分からない素数の分布が完璧に理解できる、それがリーマン予想です。このように両者には似た考えが詰まっています。しかもそれだけではありません。例えば調和振動子の分配関数とリーマンゼータ関数は具体的につながっています。実際、物理系に対してスペクトルゼータ関数(固有値から定まるディリクレ級数)を考えることは、分配関数を考えることと本質的に同じです。その橋渡しには、歴史的にも相対論と量子力学の構築とともに進歩を遂げた表現論という数学があります。
本稿では、量子相互作用を記述する系の分配関数とスペクトルゼータ関数のつながりをみていくことになりますが、物理系と数論のつながりを楽しんでいただきたいと思います。
以下、整数全体がなす整数環、有理数全体がなす有理数体、実数体、複素数体を、それぞれ ![]() で表します。
で表します。
リーマンゼータとその特殊値、保型形式
調和級数、すなわち正整数の逆数の和が発散することは古くから知られていました。しかし、逆数の平方和の値はどうなのか。1644年にボローニャの数学者メンゴリが提起したこの問いはバーゼル(オイラーの生誕地)の問題と呼ばれ、その答えが ![]() であることをオイラーが発見(1735年)するまでに90年を待ちました。当時、円周率
であることをオイラーが発見(1735年)するまでに90年を待ちました。当時、円周率 ![]() が答えに現れたことに人々は大変驚きました。以下のリーマンのゼータ関数
が答えに現れたことに人々は大変驚きました。以下のリーマンのゼータ関数 ![]() (親しみを込めてリーマンゼータと呼びます)を使えば、これらは
(親しみを込めてリーマンゼータと呼びます)を使えば、これらは ![]() と書かれます。
と書かれます。
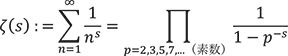
中央の級数と下段のオイラー積をつなぐ等式は、すべての整数が一意に素因数分解されるという事実を表しています。この級数や無限積の絶対収束域は、半平面![]() ですが、
ですが、![]() 、全複素平面に有理型関数として一意に解析接続され、
、全複素平面に有理型関数として一意に解析接続され、![]() のみで極(分数関数の分母が0になる状況と同じです)を持ちます。オイラーは、
のみで極(分数関数の分母が0になる状況と同じです)を持ちます。オイラーは、![]() の無限乗積とテイラー展開の2次の項を比較することでバーゼルの問題を解決したほか、一般の偶数点での値
の無限乗積とテイラー展開の2次の項を比較することでバーゼルの問題を解決したほか、一般の偶数点での値 ![]() のベルヌーイ数
のベルヌーイ数
![]() による表示
による表示
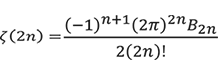
も発見しました。一方で、奇数点での値についてはそれが無理数であるかどうかさえも分からず歴史が進みました。不明の最初である ![]() の値でさえ、 1979年のロジェ・アペリーによる研究(2)まで待たねばなりませんでした。アペリーはその後アペリー数と呼ばれる不思議な数列を定義して、
の値でさえ、 1979年のロジェ・アペリーによる研究(2)まで待たねばなりませんでした。アペリーはその後アペリー数と呼ばれる不思議な数列を定義して、![]() と
と ![]() の無理数性を同じ方法で示しました。しかし現在でも、一般の奇数点における無理数性はほとんど分かっていません。実際、21世紀になりようやくタンギー・リヴォアルらが
の無理数性を同じ方法で示しました。しかし現在でも、一般の奇数点における無理数性はほとんど分かっていません。実際、21世紀になりようやくタンギー・リヴォアルらが ![]() には無理数が無数に存在すること、そして
には無理数が無数に存在すること、そして ![]() の中に少なくとも1つ無理数が存在することを示しました。その後、ワディム・ズディリンの2001年の論文により
の中に少なくとも1つ無理数が存在することを示しました。その後、ワディム・ズディリンの2001年の論文により ![]() の少なくとも1つは無理数であることが分かりました。これが現在の地球での最良の理解です。
の少なくとも1つは無理数であることが分かりました。これが現在の地球での最良の理解です。
■素数定理とリーマン予想
ガウスやルジャンドルにより予想されリーマンにより解析的な証明を示唆された次の素数定理は、1896年にド・ラ・ヴァレー・プーサンとアダマールにより示されました:![]() を
を ![]() 以下の素数の個数とすると
以下の素数の個数とすると
![]()
ここで ![]() は
は ![]() を表しています。それは、
を表しています。それは、 ![]() 上で
上で ![]() であることから従うというリーマンのアイデアによるものでした。バラバラにみえる素数の出現分布と
であることから従うというリーマンのアイデアによるものでした。バラバラにみえる素数の出現分布と ![]() の解析的性質を結びつけたリーマンの発見は、(将来に期待される)リーマン予想の解決よりも数学上の功績が大きいかもしれません。
の解析的性質を結びつけたリーマンの発見は、(将来に期待される)リーマン予想の解決よりも数学上の功績が大きいかもしれません。
■リーマンゼータの関数等式
リーマンゼータ ![]() は関数等式を満たします。
は関数等式を満たします。![]() をガンマ関数として
をガンマ関数として ![]() とおくと、それは
とおくと、それは
![]()
という反射式で与えられます。関数等式の味わいは、解析接続の概念がない頃すでにオイラーが手計算で見つけていた
![]()
などにもみて取れます。本稿では保型関数・保型形式(モジュラー形式)という非可換な群の作用によって本質的に不変となる関数を取り上げます。三角関数の場合は、平行移動不変性、つまり可換な群 ![]() の作用に関する不変性がありますので、保型関数は、三角関数の非可換版だと思うことができます。その紹介のためにも、また、分配関数との関係を述べるうえでもちょうどよいので、以下、上記の関数等式の証明の概略を紹介します。なお、現れる積分や級数は良い意味で収束しているものとします(そのようなものだけを考えます)。関数
の作用に関する不変性がありますので、保型関数は、三角関数の非可換版だと思うことができます。その紹介のためにも、また、分配関数との関係を述べるうえでもちょうどよいので、以下、上記の関数等式の証明の概略を紹介します。なお、現れる積分や級数は良い意味で収束しているものとします(そのようなものだけを考えます)。関数 ![]() のメリン変換
のメリン変換 ![]() を次で定義します。
を次で定義します。
![]()
例えば 、![]() であれば、
であれば、![]() の定義から
の定義から ![]() が分かります。そこで今、級数
が分かります。そこで今、級数 ![]() に対して
に対して ![]() と定めてメリン変換を計算すると、容易に
と定めてメリン変換を計算すると、容易に ![]() と計算できます。そこで複素上半平面
と計算できます。そこで複素上半平面 ![]() 上で定義される級数
上で定義される級数 ![]() を
を
![]()
とすると、![]() とおくとき
とおくとき ![]() が分かります。この級数
が分かります。この級数 ![]() はヤコビのテータ関数と呼ばれる保型形式です。
はヤコビのテータ関数と呼ばれる保型形式です。![]() という平行移動不変性に加えて
という平行移動不変性に加えて ![]() という関係式を満たします。後者は、関数
という関係式を満たします。後者は、関数 ![]() のフーリエ変換を
のフーリエ変換を ![]() と書くときに次のポアソン和公式
と書くときに次のポアソン和公式
![]()
に ![]() という急減少関数を代入することで容易に得られます。
という急減少関数を代入することで容易に得られます。![]() とおけば
とおけば ![]() ですので、メリン変換の定義に戻れば
ですので、メリン変換の定義に戻れば ![]() の関数等式が得られます。ここで用いたポアソン和公式には、次のような解釈ができます。時計の時刻表示に倣い、整数部分が同じ実数は同じものとみなします。それを
の関数等式が得られます。ここで用いたポアソン和公式には、次のような解釈ができます。時計の時刻表示に倣い、整数部分が同じ実数は同じものとみなします。それを ![]() と書いて円だと思いましょう。このとき、右辺はその円周を何回まわっているかの長さ(巻き数)に関する和、左辺は可換群
と書いて円だと思いましょう。このとき、右辺はその円周を何回まわっているかの長さ(巻き数)に関する和、左辺は可換群 ![]() の(既約)表現
の(既約)表現 ![]() のうちで
のうちで ![]() 上自明なもの、つまり、
上自明なもの、つまり、![]() 全体にわたる和と考えます。左辺は、
全体にわたる和と考えます。左辺は、![]() のラプラシアン
のラプラシアン ![]() の固有値と考えてもよいものです。この解釈を非可換な群とその離散部分群に拡張したものが、セルバーグの跡公式と呼ばれるものです〔
の固有値と考えてもよいものです。この解釈を非可換な群とその離散部分群に拡張したものが、セルバーグの跡公式と呼ばれるものです〔 ![]() のような可換群の既約表現はつねに1次元であり、表現の指標(トレース)は表現そのものです〕。
のような可換群の既約表現はつねに1次元であり、表現の指標(トレース)は表現そのものです〕。
■モジュラー形式・保型形式
各成分が整数(実数)であり行列式の値1の2行2列の行列全体がなす群を ![]()
![]() とします。
とします。![]() は、2つ
は、2つ ![]() と
と ![]() で生成されています〔各元が
で生成されています〔各元が ![]() と
と ![]() のいくつかの(非可換な)積で表示されるという意味です〕。さて
のいくつかの(非可換な)積で表示されるという意味です〕。さて ![]() は一次分数変換
は一次分数変換 ![]() により上半平面
により上半平面 ![]() に作用します。
に作用します。![]() は同一の作用を定めるため、モジュラー群
は同一の作用を定めるため、モジュラー群 ![]() に対し、
に対し、![]() の元の作用で移り合う
の元の作用で移り合う ![]() の点を同一視した空間
の点を同一視した空間 ![]() を考えます。これが、モジュラー形式(保型形式)が住む空間です。ただしここでは、
を考えます。これが、モジュラー形式(保型形式)が住む空間です。ただしここでは、![]() の区別は気にしないでおきます。上記の
の区別は気にしないでおきます。上記の ![]() は、ちょうど
は、ちょうど ![]() で生成される
で生成される ![]() の部分群
の部分群 ![]() の作用で(ほぼ)不変な関数であるため、
の作用で(ほぼ)不変な関数であるため、![]() 保型形式と呼ばれるものになっています。
保型形式と呼ばれるものになっています。
相互作用模型
■量子ラビ模型
量子ラビ模型(Quantum Rabi model: QRM)は光と物質の相互作用の基本モデルです。そのハミルトニアンは
![]()
ここで、 ![]() は角振動数
は角振動数 ![]() の調和振動子(ボゾンモード:光子)に対する生成消滅演算子、
の調和振動子(ボゾンモード:光子)に対する生成消滅演算子、![]() は2準位系に対するパウリ行列、
は2準位系に対するパウリ行列、![]() は2準位系と光子間の結合強度、
は2準位系と光子間の結合強度、![]() は2準位間のエネルギー差です。
は2準位間のエネルギー差です。![]() は2次元ベクトル値2乗可積分関数がなすヒルベルト空間
は2次元ベクトル値2乗可積分関数がなすヒルベルト空間 ![]() に作用します。
に作用します。![]() にバイアス項をつけた
にバイアス項をつけた ![]() は、非対称量子ラビ模型(asymmetric QRM: AQRM)を定めます。これらは共振器量子電磁力学の手法による深強結合状態の実現のための実験測定結果を予言しました(3)。
は、非対称量子ラビ模型(asymmetric QRM: AQRM)を定めます。これらは共振器量子電磁力学の手法による深強結合状態の実現のための実験測定結果を予言しました(3)。
■非可換調和振動子
非可換調和振動子(NCHO:Non commutative harmonic oscillator)(4)(5)はハミルトニアンで定まる常微分方程式系です(式(1))。![]() は
は ![]() のとき、
のとき、![]() 上の自己共役作用素となり、離散固有値
上の自己共役作用素となり、離散固有値 ![]() のみを持ちます。その重複度は高々2です。スペクトルゼータ関数
のみを持ちます。その重複度は高々2です。スペクトルゼータ関数 ![]() を考えます(
を考えます( ![]() のとき、
のとき、![]() は2個の調和振動子とユニタリ同値となり
は2個の調和振動子とユニタリ同値となり ![]() )。
)。
種々興味深いことがあります。例えば、![]() は全複素平面に有理型関数として解析接続され
は全複素平面に有理型関数として解析接続され ![]() のみに一位の極をもち、
のみに一位の極をもち、![]() と同様に負の偶数点で自明な零点を持ちます(6)。さらに、
と同様に負の偶数点で自明な零点を持ちます(6)。さらに、![]() からは自然なかたちでアペリー数の類似物が現れ、
からは自然なかたちでアペリー数の類似物が現れ、![]() では保型性や楕円曲線との明示的関連があるなど豊かな性質を有します(表)。
では保型性や楕円曲線との明示的関連があるなど豊かな性質を有します(表)。 ![]() の研究では、通常のモジュラー形式を超え、Eichiler 形式(アーベル積分の一般化)(7)を自然に拡張したものや関連する新しいコホモロジーが現れ(8)(9)その具体的記述において、一般 Eisenstein 級数(10)の微分などが生まれます。これらは、志村五郎が1982年に創始後、現在改めて進展している慨正則保型形式の研究(11)(の1変数の場合)にも深く関係しています。なお、筆者にとってのアペリー数類似に関する研究は、アペリ—の直後、
の研究では、通常のモジュラー形式を超え、Eichiler 形式(アーベル積分の一般化)(7)を自然に拡張したものや関連する新しいコホモロジーが現れ(8)(9)その具体的記述において、一般 Eisenstein 級数(10)の微分などが生まれます。これらは、志村五郎が1982年に創始後、現在改めて進展している慨正則保型形式の研究(11)(の1変数の場合)にも深く関係しています。なお、筆者にとってのアペリー数類似に関する研究は、アペリ—の直後、![]() の一般奇数点における値の無理数性の証明をめざして開拓された(成功はしなかったものの) フリッツ・ビューカーズらの数論・代数幾何的研究に触発されたところが極めて大です。
の一般奇数点における値の無理数性の証明をめざして開拓された(成功はしなかったものの) フリッツ・ビューカーズらの数論・代数幾何的研究に触発されたところが極めて大です。
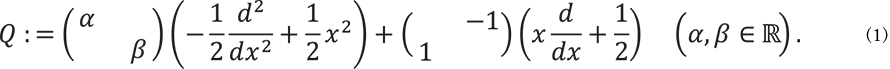

■被覆モデル
NCHOを導入した1つには、通常の表現論に現れるガウスの超幾何微分方程式の世界を広げ、系に課す対称性を少し弱めて、物理観点から調和振動子のスペクトルゼータ関数でもある ![]() の拡張を考えたいとの動機がありました。事実、表現論を用いることで、NCHOの固有値問題は3点
の拡張を考えたいとの動機がありました。事実、表現論を用いることで、NCHOの固有値問題は3点 ![]() を確定特異点に持つ超幾何を越えて、4点
を確定特異点に持つ超幾何を越えて、4点 ![]() を確定特異点に持つ Heun ODEの、
を確定特異点に持つ Heun ODEの、![]() を含み
を含み ![]() を含まない複素領域における正則関数の存在と同等であることが導かれます(12)(13)。 さらには、この方程式において、特異点
を含まない複素領域における正則関数の存在と同等であることが導かれます(12)(13)。 さらには、この方程式において、特異点 ![]() と
と ![]() を合流させることにより、QRMの固有値問題と、その整関数解の存在が同値であることが知られていた合流型Heun 方程式が得られることも分かりました。この関係は、NCHOが、それぞれの Heun描像を見ることで、QRMのいわば被覆モデル(13)であることを示しています。この被覆関係は、η-NCHOとAQRMにおいても同様です(14)(15)。被覆モデル間の数論的性質の伝播、あるいはそのファイバの研究は興味深い問題です。さらにごく最近になり、NCHOが2光子量子ラビ模型(16)という伝統的な物理模型を与えているという事実が導かれました(17)。つまり、1光子と2準位原子の相互作用(QRM)は、2光子と2準位原子のそれから得られるという事実の発見といえます。このような物理模型間に生まれた被覆という数学概念が、実際の実験により確認できるものかどうかは分かりませんが、興味津々です。また 参考文献(17)では、この場合の被覆関係が、表現論的により明確になったことも特筆されます。
を合流させることにより、QRMの固有値問題と、その整関数解の存在が同値であることが知られていた合流型Heun 方程式が得られることも分かりました。この関係は、NCHOが、それぞれの Heun描像を見ることで、QRMのいわば被覆モデル(13)であることを示しています。この被覆関係は、η-NCHOとAQRMにおいても同様です(14)(15)。被覆モデル間の数論的性質の伝播、あるいはそのファイバの研究は興味深い問題です。さらにごく最近になり、NCHOが2光子量子ラビ模型(16)という伝統的な物理模型を与えているという事実が導かれました(17)。つまり、1光子と2準位原子の相互作用(QRM)は、2光子と2準位原子のそれから得られるという事実の発見といえます。このような物理模型間に生まれた被覆という数学概念が、実際の実験により確認できるものかどうかは分かりませんが、興味津々です。また 参考文献(17)では、この場合の被覆関係が、表現論的により明確になったことも特筆されます。
■分配関数とスペクトルゼータ関数
自己共役作用素 ![]() をハミルトニアンに持つ量子系を考えます。このとき知りたいのはユニタリ作用素
をハミルトニアンに持つ量子系を考えます。このとき知りたいのはユニタリ作用素 ![]() (プロパゲータ/熱核)であり、そのトレースである分配関数
(プロパゲータ/熱核)であり、そのトレースである分配関数 ![]() です。分配関数は Boltzmann 因子
です。分配関数は Boltzmann 因子 ![]() は状態
は状態 ![]() のエネルギー:固有値) の総和として式(2)で与えられます。
のエネルギー:固有値) の総和として式(2)で与えられます。
ここで ![]() は可能なすべての固有状態を表しています。一方、 系のスペクトルゼータ関数
は可能なすべての固有状態を表しています。一方、 系のスペクトルゼータ関数 ![]() とは、固有値列
とは、固有値列 ![]() (簡単のため
(簡単のため ![]() としておきます)から定まる次のディリクレ級数です(式(3))。
としておきます)から定まる次のディリクレ級数です(式(3))。
したがって、![]() の定義から、両者は Mellin変換でつながります(式(4))。
の定義から、両者は Mellin変換でつながります(式(4))。
ところで、長く待たれていたQRMやAQRMの熱核とそのトレースである分配関数の解析的公式が、ようやく得られました(18)〜(20)。その方法は、ファインマン経路積分の数学的厳密形と考えられているトロッター・加藤 の積公式を用い、ガウス型積分を実行し、さらに ![]() (
( ![]() は2元体)のヴェイユ表現に着目した
は2元体)のヴェイユ表現に着目した ![]() 上のフーリエ変換を利用するというものです。さらに、公式に現れる級数が無限対称群
上のフーリエ変換を利用するというものです。さらに、公式に現れる級数が無限対称群 ![]() の
の ![]() への作用の既約表現分解の和に相当し、各項が
への作用の既約表現分解の和に相当し、各項が ![]() の軌道積分で与えられることも分かりました。これは驚きであり、より一般のモデルへのヒントになります。またこれにより、対応するスペクトルゼータ関数(一般にフルビッツ型)の無限遠点から原点を廻る周回積分表示を用いた解析接続やベルヌーイ数の拡張(Rabi-Bernoulli 数)も得られます。ここで注意すべきは、このRabi-Bernoulli 数の母関数が原点でのローラン展開であることから分配関数が復元できることです。一方で、NCHOについては、正の整数点における特殊値の代数的な関数の積分表示は得られますが、分配関数は得られていません。ただし、負の整数点での値も、やはりベルヌーイ数の拡張(NC-Bernulli数)としてとらえられます。したがってQRMの場合と同様、NC-Bernulli数の母関数が原点においてローラン展開をもてば、それがNCHOの分配関数を与えます。しかしながら現時点では、強い傍証はあるものの予想(21)の段階を越えません。一方で、予想に関連して収束の問題を吟味したところ、分配関数を用いて形式的に得られるゼータ関数のいわゆるボレル和による評価や、非アルキメデス的考察が有用なことも分かってきました。実際、
の軌道積分で与えられることも分かりました。これは驚きであり、より一般のモデルへのヒントになります。またこれにより、対応するスペクトルゼータ関数(一般にフルビッツ型)の無限遠点から原点を廻る周回積分表示を用いた解析接続やベルヌーイ数の拡張(Rabi-Bernoulli 数)も得られます。ここで注意すべきは、このRabi-Bernoulli 数の母関数が原点でのローラン展開であることから分配関数が復元できることです。一方で、NCHOについては、正の整数点における特殊値の代数的な関数の積分表示は得られますが、分配関数は得られていません。ただし、負の整数点での値も、やはりベルヌーイ数の拡張(NC-Bernulli数)としてとらえられます。したがってQRMの場合と同様、NC-Bernulli数の母関数が原点においてローラン展開をもてば、それがNCHOの分配関数を与えます。しかしながら現時点では、強い傍証はあるものの予想(21)の段階を越えません。一方で、予想に関連して収束の問題を吟味したところ、分配関数を用いて形式的に得られるゼータ関数のいわゆるボレル和による評価や、非アルキメデス的考察が有用なことも分かってきました。実際、![]() では発散する特殊値表示が、
では発散する特殊値表示が、 ![]() 進
進 ![]() の世界では
の世界では ![]() 進フルビッツゼータ関数(22)の特殊値としてとらえられるのです(21)。
進フルビッツゼータ関数(22)の特殊値としてとらえられるのです(21)。
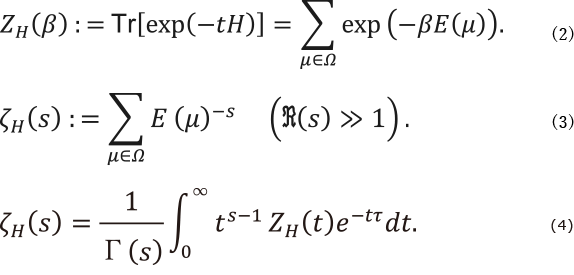
L-関数と分配関数の零点構造
表は ![]() と
と ![]() を対比したものです。前者では
を対比したものです。前者では ![]() とすれば後者になるわけですが、大切なことは、後者だけでは見えなかった構造が前者によって浮かび上がってきていることです。
とすれば後者になるわけですが、大切なことは、後者だけでは見えなかった構造が前者によって浮かび上がってきていることです。![]() に対してはオイラー積も関数等式も期待できません。しかし、正整数点における特殊値の代数関数による積分和表示(9)からは、
に対してはオイラー積も関数等式も期待できません。しかし、正整数点における特殊値の代数関数による積分和表示(9)からは、![]() が、数論的なL-関数(表現に付随するゼータ関数)の級数和であることが予想されています。仮にこの予想が正しければ、
が、数論的なL-関数(表現に付随するゼータ関数)の級数和であることが予想されています。仮にこの予想が正しければ、![]() は、各項がオイラー積を持つとしても、全体としてはオイラー積を持ちません。関数等式についても、関数等式の対称軸(
は、各項がオイラー積を持つとしても、全体としてはオイラー積を持ちません。関数等式についても、関数等式の対称軸( ![]() ならば直線
ならば直線 ![]() )が異なるL-関数の項があれば成立しないことに矛盾はありません。
)が異なるL-関数の項があれば成立しないことに矛盾はありません。
他方、零点といえば関連して興味深いことの1つに、強磁性イジング模型の分配関数(式(5))の零点がすべて虚数( ![]() とおけば単位円周上)であるというリー・ヤンの円定理(1952)があります(23)。この定理には、さまざまな拡張があります。もちろんそれは、分配関数の零点の前後で相転移が起こるからです。ゼータ関数や L-関数の零点研究は、グロタンディークの代数幾何の革新を促した有限体版のリーマン予想と見做せるヴェイユ予想、そして、保型形式
とおけば単位円周上)であるというリー・ヤンの円定理(1952)があります(23)。この定理には、さまざまな拡張があります。もちろんそれは、分配関数の零点の前後で相転移が起こるからです。ゼータ関数や L-関数の零点研究は、グロタンディークの代数幾何の革新を促した有限体版のリーマン予想と見做せるヴェイユ予想、そして、保型形式 ![]() に対するL-関数(式(6))の(逆数の)零点の絶対値に関する ラマヌジャン予想 “
に対するL-関数(式(6))の(逆数の)零点の絶対値に関する ラマヌジャン予想 “ ![]() ”が20世紀の数論研究を牽引しました。一方、分配関数・保型形式側では、例えば Eisenstein級数の零点研究は進みましたが、その意義はまだ必ずしも明確ではありません。相転移という観点からより深い研究が進むことが望まれます。また、このイジング模型のサイト数
”が20世紀の数論研究を牽引しました。一方、分配関数・保型形式側では、例えば Eisenstein級数の零点研究は進みましたが、その意義はまだ必ずしも明確ではありません。相転移という観点からより深い研究が進むことが望まれます。また、このイジング模型のサイト数 ![]() を無限にしたときの偏角分布の研究は、
を無限にしたときの偏角分布の研究は、![]() の零点の偏角分布に関する佐藤-テイト予想に類似していて数学的にも興味深いものです。また、佐藤-テイト予想についても、これまでの正則保型形式-数論幾何を超えて非正則、特にセルバーグ跡公式で重要なマース形式などの研究の進展が強く望まれています。非正則な保型形式については堀永が、またその1つのベースとなる表現論からの研究およびNCHOの多変数化に向けた研究(15)が中濱により進んでいます。後者は、不変式論についての現代的思想であり保型形式への応用もある ロジャー・エヴァンス・ハウの dual pair の理論(24)にのっとった成果です。
の零点の偏角分布に関する佐藤-テイト予想に類似していて数学的にも興味深いものです。また、佐藤-テイト予想についても、これまでの正則保型形式-数論幾何を超えて非正則、特にセルバーグ跡公式で重要なマース形式などの研究の進展が強く望まれています。非正則な保型形式については堀永が、またその1つのベースとなる表現論からの研究およびNCHOの多変数化に向けた研究(15)が中濱により進んでいます。後者は、不変式論についての現代的思想であり保型形式への応用もある ロジャー・エヴァンス・ハウの dual pair の理論(24)にのっとった成果です。
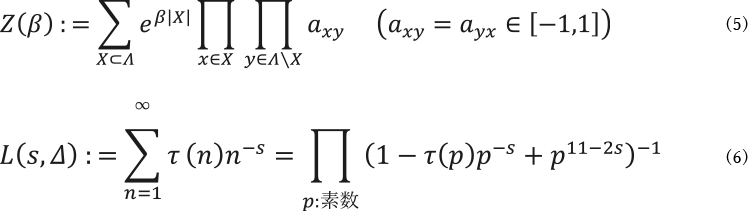
■参考文献
(1) E.T. Jaynes and F.W. Cummings:“Comparison of quantum and semiclassical radiation theories with application to the beam maser,“ Proc. IEEE, Vol. 51, pp. 89 -109, 1963.
(2) R. Apéry:“Irrationalité de ζ(2) et ζ(3),”Astérisque., Vol. 61, pp. 11-13, 1979.
(3) 布施・吉原・角柳・仙場:“超伝導人工原子と電磁場の相互作用〜強結合のその先へ〜,”「最近の研究から」,日本物理学会誌,Vol. 73, pp. 21-26, 2018.
(4) A. Parmeggiani and M. Wakayama:“Oscillator representations and systems of ordinary differential equations,”Proc. Natl. Acad. Sci. USA, Vol. 98, pp. 26–30, 2001.
(5) A. Parmeggiani:“Spectral Theory of Non-commutative Harmonic Oscillators: An Introduction,”Lecture Notes in Math., Vol. 1992, Springer, 2010.
(6) T. Ichinose and M. Wakayama:“Zeta functions for the spectrum of the non-commutative harmonic oscillators,” Comm. Math. Phys., Vol. 258, pp. 697-739, 2005.
(7) R. C. Gunning:“The Eichler cohomology groups and automorphic forms,” Trans. Amer. Math. Soc., Vol. 100, pp. 44-62, 1961.
(8) K. Kimoto and M. Wakayama:“Elliptic curves arising from the spectral zeta function for non-commutative harmonic oscillators and Γ0(4)-modular forms,”in Proc. Conf. L-functions, World Scientific, pp. 201-218, 2007.
(9) K. Kimoto and M. Wakayama:“Apéry-like numbers for non-commutative harmonic oscillators and automorphic integrals,”Ann. Inst. H. Poincaré D, Vol. 10, pp. 205-275, 2023.
(10) B. C. Berndt:“Generalized Eisenstein series and modified Dedekind sums,” J. Reine Angew. Math., Vol. 272, pp. 182-193, 1974.
(11) S. Horinaga:“On the representations generated by Eisenstein series of weight 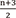 ,”J. Number Theory., Vol. 201, pp. 206-227, 2019.
,”J. Number Theory., Vol. 201, pp. 206-227, 2019.
(12) H. Ochiai:“Non-commutative harmonic oscillators and Fuchsian ordinary differential operators,”Comm. Math. Phys., Vol. 217, pp. 357-373, 2001.
(13) M. Wakayama:“Equivalence between the eigenvalue problem of non-commutative harmonic oscillators and existence of holomorphic solutions of Heun differential equations, eigenstates degeneration and the Rabi model,”Int. Math. Res. Notices, Vol. 145, pp. 759-794, 2016.
(14) C. Reyes-Bustos and M. Wakayama:“Covering Families of the Asymmetric Quantum Rabi Model:η-Shifted Non-commutative Harmonic Oscillators,”Comm. Math. Phys., Vol. 403, pp. 1429-1476, 2023.
(15) R. Nakahama:“Representation theory of 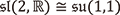 and a generalization of non-commutative harmonic oscillators,”in Mathematical Foundation for Post-Quantum Cryptography,“Mathematic for Industry”Springer, 2024. arXiv: 2310. 17118
and a generalization of non-commutative harmonic oscillators,”in Mathematical Foundation for Post-Quantum Cryptography,“Mathematic for Industry”Springer, 2024. arXiv: 2310. 17118
(16) D. Braak:“Spectral Determinant of the Two-Photon Quantum Rabi Model,”Ann. Phys., Vol. 535, p.2200519, 2023.
(17) R. Nakahama:“Equivalence between non-commutative harmonic oscillators and two-photon quantum Rabi models,”Preprinnt 2024. arXiv: 2405. 19814
(18) C. Reyes-Bustos and M. Wakayama:“The heat kernel for the quantum Rabi model,”Adv. Theor. Math. Phys., Vol. 5, pp. 1347-1447, 2022.
(19) C. Reyes-Bustos and M. Wakayama:“Heat kernel for the quantum Rabi model:II. Propagators and spectral determinants,”J. Phys. A:Math. Theor., Vol. 54, p. 115202, 2021.
(20) C. Reyes-Bustos:“The heat kernel of the asymmetric quantum Rabi model,”J. Phys. A:Math. Theor., Vol. 56, p. 425302, 2023.
(21) K. Kimoto and M. Wakayama:“Partition functions for non-commutative harmonic oscillators and related divergent series,”Indag. Math., 2024.
https://doi.org/10.1016/j.indag.2024. 05.011
(22) H. Cohen:“Number Theory Volume II:Analytic and Modern Tools,”Springer, 2007.
(23) D. Ruelle:“Statistical Mechanics:Rigorous Results,”Addison-Wesley, 1989.
(24) R. Howe:“Remarks on classical invariant theory,”Trans. Ameri. Math. Soc., Vol. 313, pp. 539-570, 1989.

(左から)Cid Reyes-Bustos/若山 正人







数学は言葉の学問です。物理にしても人間が使う自然言語では到底表現しきれません。論理を駆使しても不足です。そのような中、存在しているがひっそりと隠れている数学の世界を、関心ある問題から探る様子を垣間みていただけたなら望外の喜びです。