2019年9月号
限界まで効率良くメッセージを送れます ―― シャノン限界を達成する通信路符号
- 情報理論
- 通信路符号
- CoCoNuTS
本稿では、通信効率の限界(シャノン限界)を達成する実行可能な符号化技術CoCoNuTSを用いて構成した通信路符号(誤り訂正符号)を紹介します。本技術により既存の方法よりも効率の良い通信が実現できます。
村松 純(むらまつ じゅん)
NTT コミュニケーション科学基礎研究所
通信路符号
通信を行ううえでは、雑音のある環境下でも正しくメッセージ(情報)を伝える必要があります。これを実現する技術は「通信路符号」あるいは「誤り訂正符号」と呼ばれており、光通信や無線通信に限らず、計算機の内部やハードディスク・光ディスク等の記録装置、スマートフォン等で情報を読み取るための二次元コード等に応用されています。あらゆる通信機器の中に入っているといっても過言ではありません。
雑音のある環境(通信路)が与えられたとき、正しくメッセージを伝えることができる効率には限界があります。このような通信効率の限界は、1948年にこれを発表した計算機科学者シャノンにちなんで「シャノン限界*1」と呼ばれています。しかしながら、シャノンが提案した符号は膨大な計算量を必要としていたため、その実行は困難でした。実行可能なシャノン限界を達成する符号の構成は、シャノンが創始した情報理論の70年にわたる課題です。
その後、シャノン限界を達成する実用的な符号としてLDPC(Low Density Parity Check:低密度パリティ検査)符号*2などが開発され、近年の第5世代移動通信システム(5G)に実装されています。しかしながら、これらの符号がシャノン限界を達成するのはある特殊な通信路に限られており、一般の通信路では限界を達成できません。
*1 シャノン限界:通信路符号(誤り訂正符号)の文脈においては「通信路容量」という名称として知られているものです。
*2 LDPC符号:「パリティ検査行列」と呼ばれる低密度行列(成分のほとんどが0の行列)を用いて高速な復号を行います。
研究の成果
NTTコミュニケーション科学基礎研究所では、シャノン限界を達成する符号化技術CoCoNuTS(Code based on Constrained Numbers Theoretically-achieving the Shannon limit:拘束条件を満たす系列に基づくシャノン限界を達成する符号)*3を開発しました。本技術を用いることにより、通信路符号だけでなく、情報源符号や情報理論的安全性を持つ暗号などの通信のあらゆる問題に対して、限界を達成と実行可能性を両立させる符号を構築できます。今回は、本技術を通信路符号へ応用することにより、それがシャノン限界を達成できることを数学的に証明しました(1)(2)(3)。また、シミュレーション実験により、従来のLDPC符号ではシャノン限界を達成できなかった通信路に対して、提案法が従来法を超える性能を持つことを確認しました。
*3 CoCoNuTS:「拘束条件を満たす乱数生成器」を用いることにより限界を達成する通信を実現することから名付けました。
技術のポイント
通信路符号(誤り訂正符号)が実現する通信システム
通信路符号が実現する通信システムを図1に示します。ここでは通信会社の基地局がメッセージを送信する送信者となり、スマートフォンを持ったユーザが受信者となっています。最初に符号器は送信したいメッセージMを符号化して通信路入力Xへ変換します。変換された信号は電波に変換(変調)されて送信されますが、電波を送受信して通信路に出力Yを得る際に雑音が混入することを想定します。復号器は通信路出力Yから元の再生メッセージM'を復元します。ここで、正しい通信とは、メッセージと再生メッセージが同一(M=M')であることを意味しています。そこで、メッセージと再生メッセージが異なる(M≠M')事象の確率を「復号誤り確率」と定義します。この値が小さいほど性能が良いことになります。一方で、符号化レートをメッセージシンボル数と送信信号数の比と定義します。この比が大きいほど通信効率は高くなり、高速な通信が可能になりますが、通信効率を大きくし過ぎると復号誤り確率を0に近づけることができなくなります。この通信システムでは、復号誤り確率が0に限りなく近いような符号化・復号化で、可能な限り大きな符号化レートを実現することをめざします。
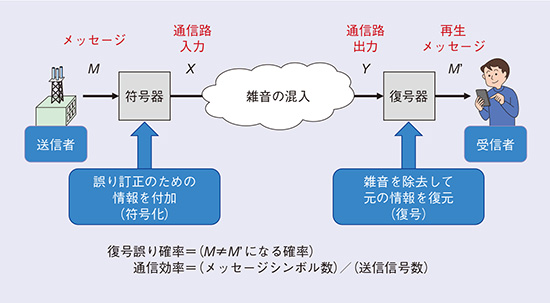
図1 通信路符号が実現する通信システム
符号化の具体例
メッセージ “01” を送信することを例にして、符号化の具体的な方法を図2に示します。符号器はメッセージ “01” を符号化して通信路入力 “01011” を求めています。この符号器では、メッセージを2回繰り返した後でメッセージの左右の2ビットの加えた「検算ビット」(排他的論理和)を付加するという操作を行っています。この例では、受信時にノイズが混入して “01111” という通信路出力が得られました。復号器は符号化のルールからノイズが混入した位置を特定して、再生メッセージ “01” を得ます。この手続きが復号と呼ばれるものです。今回は正しいメッセージと再生メッセージが一致して正しい通信が行われましたが、雑音によっては正しくメッセージが再生できない場合もあります。この例では、2ビットのメッセージを5ビットの通信路入力へ変換したので、符号化レートは2/5=0.4になります。この例にあるメッセージの繰り返し回数や検算ビットを増やすことにより、より多くの雑音の位置を特定できるようになりますが、送信信号数が増えるため符号化レートは小さくなってしまいます。高速な通信のためには、雑音の位置を高い確率で特定できて、かつ符号化レートを可能な限り大きくできることが重要です。
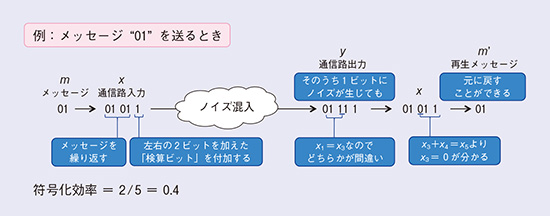
図2 符号化の具体例
シャノン限界
図3はシャノン限界(通信路容量)を説明しています。図1では、符号が満たすべき条件として、復号誤り確率が0に限りなく近いことを要請しました。一方で、符号化レートが大きい符号ほど通信効率が良いことを説明しました。シャノン限界は復号誤りが0に限りなく近い符号の符号化レートの限界です。シャノンは符号化レートの限界が図3に示されている式に等しいことを示しました。この限界は送信信号数を十分に大きくとることによって達成できます。シャノン限界を超えた効率を持つ符号を設計することは理論上不可能であり、もしもこの限界を達成する方法が実現できれば、理論的にはこれ以上の性能向上が見込めないことになります。なお、シャノン限界を達成するためには、通信路入力分布Pを最適化する必要があります。
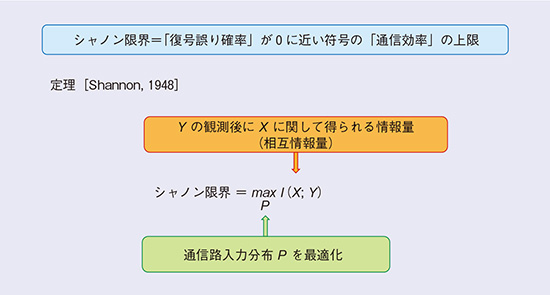
図3 シャノン限界
提案法CoCoNuTSの技術ポイント
CoCoNuTSを用いた通信路符号の構成を図4に示します。提案法では、2つの疎行列(成分のほとんどが0の行列)A、Bとベクトルcを用いて構成しています。さらに符号器と復号器に現れる写像 fA、B、gA (図4の赤枠の部分)として、後述の「拘束条件を満たす乱数生成器」を用いて最適な通信路入力分布Pを実現することにより、シャノン限界を達成することができるようになりました。これは図4に示されている定理を証明することによって理論的に保証されます(2)、(3)。
従来法であるLDPC符号では、生成行列を用いて、メッセージと通信路入力を対応させます。このため、得られる通信路入力の分布は一様分布に近いものになります。したがって、図3で示したシャノン限界の式で、通信路入力分布Pが一様分布のときに最大値(max)を達成していれば、LDPC符号はシャノン限界を達成しているといえます。逆に、最大値を達成する通信路入力分布Pが一様分布ではない場合はシャノン限界を達成できないことが分かります。
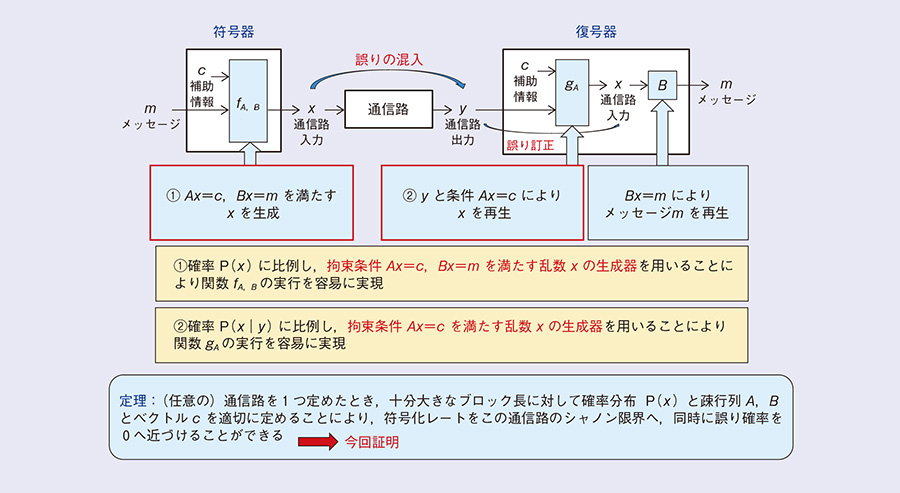
図4 提案法CoCoNuTSの技術ポイント
拘束条件を満たす乱数生成器
図4の①、②では、「拘束条件を満たす乱数生成器」を用いています。これは、方程式で与えられた拘束条件を満たす系列xを与えられた確率に比例して生成させるものです。これによって、写像 fA、BとgAの実現が容易になります。ここで高次元の乱数xを直接生成する代わりに、系列の成分(一次元)の乱数の確率分布を求めて逐次的に発生させることにより、計算の実行が可能になりました(2)。
シミュレーション実験
シミュレーション実験で提案法とLDPC 符号を比較した結果を図5に示します。グラフの横軸は符号化レートを示しており、右にあるほど性能が良いことになります。グラフの縦軸は復号誤り確率を示しており、下にあるほど性能が良いことになります。グラフは提案法がLDPCよりも良い性能を持つことを示しています。例えば、縦軸の誤り確率10-4で両者を比較したとき、提案法は符号化レートで0.03、情報量に換算すると2000ビット当り60ビットの情報を多く送信できることが分かります。
符号化レートを固定して両者を比較したものを図6に示します。図5にある実験条件で符号化レート0.6の符号化を1200回繰り返したときに、復号に失敗した場合を黒点で示して頻度を可視化しました。LDPC符号では7回の復号誤りを観測したのに対して、提案法は一度も復号誤りを観測しませんでした。この結果から、同じ雑音環境で同じ量のメッセージを送信した場合は、提案法は従来法に比べてより信頼性が高いことが分かります。
提案法と従来法を実際の通信に近い状況で実行した場合の比較結果を図7に示します。実際の通信は復号誤りがないことを想定して画像を圧縮したうえで符号化しています。このため1カ所でも復号誤りが起こればファイルが破壊され、画像の大部分は再生不可能となります。符号化レート0.5では、提案法も従来法のLDPC符号も正しく復号が行われていますが、符号化レート0.6のLDPC符号では、復号誤りが発生してファイルが破壊されていることが観測できました。このことからLDPC符号による符号化の限界は0.5と0.6の間にあり、提案法はそれを超える性能を持つことが確認できます。

図5 シミュレーション実験
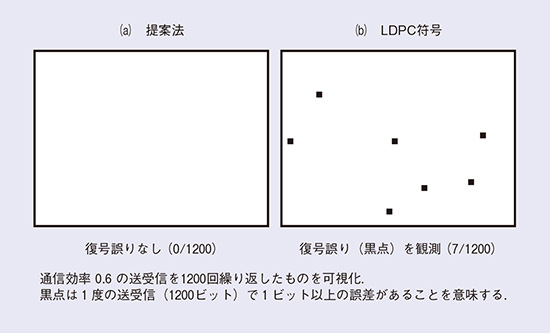
図6 通信効率をそろえて比較
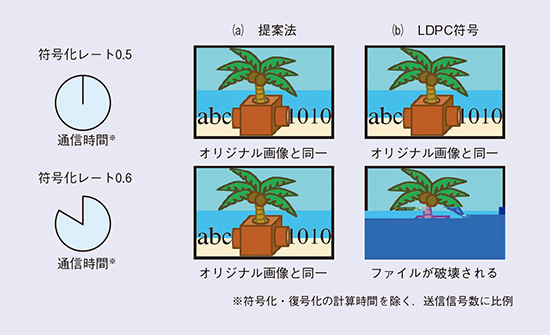
図7 圧縮画像(JPEG)を符号化して比較
今後の展開
今回実現した技術について、今後、実装のための周辺技術の確立を進め、実環境においてより高速な通信を実現するための要素技術として、本技術の応用の検討を進めます。
■参考文献
(1) J. Muramatsu and S. Miyake:“Concept of CoCoNuTS、”Proc. of AEW10 , p.4, Boppard, Germany, June 2017。
(2) J. Muramatsu:“Channel coding and lossy source coding using a generator of constrained random numbers、”IEEE Transactions on Information Theory, Vol.60, No.5, pp.2667-2686, 2014。
(3) J. Muramatsu and S. Miyake:“Channel code using constrained-random-number generator revisited、”IEEE Transactions on Information Theory, Vol.65, No.1, pp.500-508, 2019。

村松 純
問い合わせ先
NTTコミュニケーション科学基礎研究所
協創情報研究部 知能創発環境研究グループ
TEL 0774-93-5020
FAX 0774-93-5026
E-mail cs-liaison-ml@hco.ntt.co.jp




車に例えると、情報理論は通信や情報処理の「エンジン」の研究になります。普段見ることはありませんが、エンジンがなければ車は走りません。当研究所では新しい「エンジン」の原理を生み出すことをめざしています。