2024年7月号
特集
モチーフ理論――数・形・圏の織りなす抽象絵画
- 数論幾何
- コホモロジー
- モチーフ
数論幾何では、数論の問題を代数多様体という図形(幾何的対象)の問題に変換して研究します。代数多様体の情報は、コホモロジーを用いれば線形代数的なデータとして抽出できます。抽出する情報に応じて多様な種類のコホモロジーがつくられていますが、それらは「モチーフ」という普遍的な対象により背後で結び付けられていると考えられています。本稿ではモチーフ理論の概要と、執筆者らによるモチーフ理論の一般化の試みについて解説します。
宮﨑 弘安(みやざき ひろやす)
NTT基礎数学研究センタ
モチーフとは
数学ではしばしば、一見全く異なる現象・対象が驚くべき結び付きを示します。単なる奇跡のようにみえるこの結び付きの背後には、時として未知の数学的構造が隠されています。モチーフは、数論幾何に現れるさまざまな「コホモロジー」の背後に存在すると期待される数学的構造です。筆者は共同研究者たちとともに、より理想的なモチーフの理論を求めて研究を続けてきました。
数論幾何
数論幾何の枠組みを用いると、数論の研究の多くは「代数多様体」という幾何的な対象の研究に置き換えることができます。代数多様体の素朴な例は方程式のグラフです。例えば、![]() のグラフとして現れる放物線は代数多様体です。方程式の変数が少ない場合、代数多様体は「目に見え」ます。しかし、変数が増えると代数多様体は高次元になり、私たちの目には見えなくなります。また、次元が低い場合でも、構造が複雑な代数多様体を「目で見て」研究することには限界があります。
のグラフとして現れる放物線は代数多様体です。方程式の変数が少ない場合、代数多様体は「目に見え」ます。しかし、変数が増えると代数多様体は高次元になり、私たちの目には見えなくなります。また、次元が低い場合でも、構造が複雑な代数多様体を「目で見て」研究することには限界があります。
不変量──カタチを「量」とみなすには
図形を「目で見て」調べることが難しい場合、「不変量」を用いることが有効です。不変量は図形の特徴を「量」として表したものです。例えば、曲面の重要な不変量の例として穴の個数(図1)があります(穴の個数は「種数」とも呼ばれます)。もちろん、種数は曲面の特徴の一部に過ぎませんが、次の非常に重要な性質を持ちます。
•定理:曲面を連続的に変形しても種数(穴の個数)は不変である。
曲面をやわらかいゴムとみなして(破らないように)変形することを「連続変形する」と言います。この定理の応用として、図1(a)を図1(b)に連続変形できるかどうか、という問題を考えましょう。図1(a)の種数は2、図1(b)の種数は3です。一方、定理により、図1(a)をどのように連続的に変形しても種数は2のままで、決して3にはなりませんから、図1(a)は図1(b)に連続変形できないことが分かります。
この例で扱った図形の構造はシンプルなので、穴の個数が連続変形で変わらないことは直感的に明らかかもしれません。しかし、穴の数が増えたらどうでしょう。1兆個の穴を持つ曲面があるとき、それをどんなに変形しても穴の数が増えたり減ったりしない、という事実は直感的に明らかでしょうか(少なくとも筆者は1兆個の穴を持つ図形を全くイメージできません)。このような「直感の及ばない」ケースにおいても決して変化しないと数学的に証明されているところが、種数の素晴らしい点です。

見えない図形を「見る」には
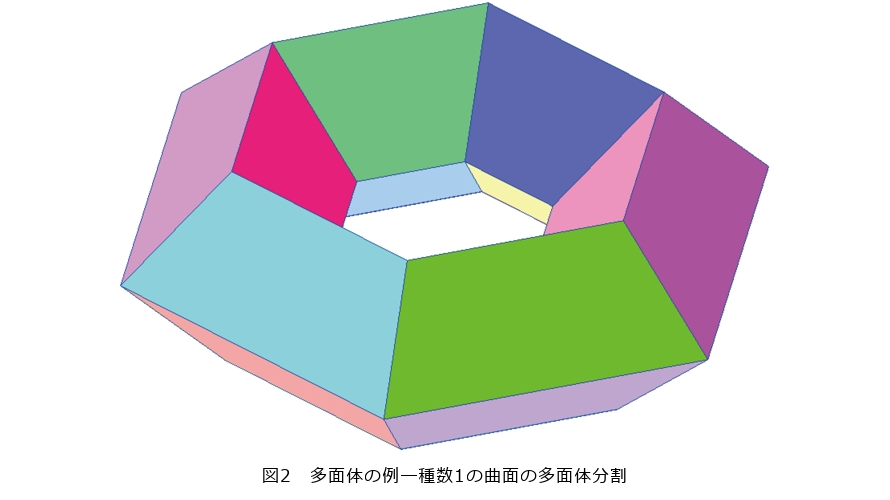
前述の例では、私たちは種数を「目で見て数え」ました。このままでは「見えない」図形の研究には役立ちそうにありません。そこで、種数を計算する別の方法を考えてみましょう。種数は連続変形で変わりませんから、曲面を図2のような多面体に変形してみましょう。このとき、次の驚くべき定理が成り立ちます。
•多面体定理:穴が ![]() 個の多面体に対し「(頂点の数)−(辺の数)+(面の数)=
個の多面体に対し「(頂点の数)−(辺の数)+(面の数)= ![]() 」が成り立つ。
」が成り立つ。
左辺の「(頂点の数)−(辺の数)+(面の数)」を多面体の「オイラー標数」と呼びます。一方、![]() は曲面の種数です(種数=genusの頭文字をとっています)。先ほどの多面体分割を例にとると、頂点、辺、面の個数は、それぞれ24個、48本、24個です。一方、種数は
は曲面の種数です(種数=genusの頭文字をとっています)。先ほどの多面体分割を例にとると、頂点、辺、面の個数は、それぞれ24個、48本、24個です。一方、種数は ![]() です。これを定理の式に代入すると、両辺はどちらも0となり、確かに一致します。
です。これを定理の式に代入すると、両辺はどちらも0となり、確かに一致します。
この例の場合、私たちは「図形の全体を外側から見て」いるので、穴の数がすぐに分かります。しかし、私たちがこの図形の表面に住んでいるとすると、穴の数を直接数えることは難しいでしょう。それでも多面体定理を使えば、図形の表面を這い回って多面体分割し、頂点・辺・面の個数を数え上げさえすれば、穴の数が計算できるのです。
この方法を発展させると高次元の図形の情報もとらえることができます。多面体は頂点・辺・面という「部品」からなります。この部品は「セル」とも呼ばれます。一般に、![]() 次元の円盤に連続的に変形できる図形を「
次元の円盤に連続的に変形できる図形を「 ![]() 次元セル」と呼びます。「頂点」は0次元の円盤(点)ですから0次元セルです。同様に、辺は1次元のセル、面は2次元のセルです(多面体の面は角張っていますが、円盤に連続変形できます)。セルを組み合わせてできる図形を「セル複体*1」と呼びます(多面体は2次元のセル複体です)。曲面を多面体に連続変形できるように、高次元の図形の多くはセル複体に変形できます*2。そして、そこに現れるセルの個数やセルどうしのつながり方を調べれば、高次元の「見えない図形」の情報が得られます。
次元セル」と呼びます。「頂点」は0次元の円盤(点)ですから0次元セルです。同様に、辺は1次元のセル、面は2次元のセルです(多面体の面は角張っていますが、円盤に連続変形できます)。セルを組み合わせてできる図形を「セル複体*1」と呼びます(多面体は2次元のセル複体です)。曲面を多面体に連続変形できるように、高次元の図形の多くはセル複体に変形できます*2。そして、そこに現れるセルの個数やセルどうしのつながり方を調べれば、高次元の「見えない図形」の情報が得られます。
*1 セル複体:胞体複体ともいいます。
*2 セル複体に分割できる図形(位相空間)をCW複体といいます。応用上現れる位相空間の多くはCW複体です。
コホモロジー
多面体定理に現れるオイラー標数は、セル複体に現れる各次元のセルの個数だけに依存しており、セルどうしの「つながり方」の情報は使っていません。つながり方の情報も加味すると、オイラー標数を大幅に改良した「セル・コホモロジー*3」が得られます。オイラー標数は図形に対し「数値」を対応させる不変量ですが、セル・コホモロジーは図形に対し「線型空間*4」を対応させます。
以下では、調べたい図形を ![]() という文字で表し、
という文字で表し、![]() の次元を
の次元を ![]() と書きましょう。図形
と書きましょう。図形 ![]() をセル複体に分割すると0次元、1次元、……、
をセル複体に分割すると0次元、1次元、……、 ![]() 次元の、合計
次元の、合計 ![]() 種類のセルが現れます。セル・コホモロジーは、セル複体に現れるセルの種類に対応して
種類のセルが現れます。セル・コホモロジーは、セル複体に現れるセルの種類に対応して ![]() 個の線型空間の集まり
個の線型空間の集まり
![]()
として与えられます。毎回これを書くのは大変なので、以下ではこの集まりを ![]() と略記しましょう。次元が2、つまり曲面の場合、セル・コホモロジーは
と略記しましょう。次元が2、つまり曲面の場合、セル・コホモロジーは ![]() という3つの線型空間からなります。線型空間からは「次元」という数値を抽出できますが、多面体定理に現れるオイラー標数は、この3つの線型空間の次元の交代和*5に一致します。このように、セル・コホモロジーの次元にはオイラー標数の情報が含まれています。
という3つの線型空間からなります。線型空間からは「次元」という数値を抽出できますが、多面体定理に現れるオイラー標数は、この3つの線型空間の次元の交代和*5に一致します。このように、セル・コホモロジーの次元にはオイラー標数の情報が含まれています。
*3 セル・コホモロジー:胞体コホモロジーとも呼ばれます。セル複体に分割できない空間にも適用可能な、より一般化されたコホモロジー理論として「特異コホモロジー」があります。
*4 線型空間:「加法・減法・スカラー倍」が適切に定まっている集合のこと。どんな線型空間も、基底を固定することで、いくつかの数値の組(数ベクトル)の集まりとして表示できます。
*5 交代和:番号付けられた数値を、1つ番号が進むごとに符号を変えて足し合わせること。この例の場合、![]() の次元をそれぞれ
の次元をそれぞれ ![]() とすれば、交代和は
とすれば、交代和は ![]() のこと。
のこと。
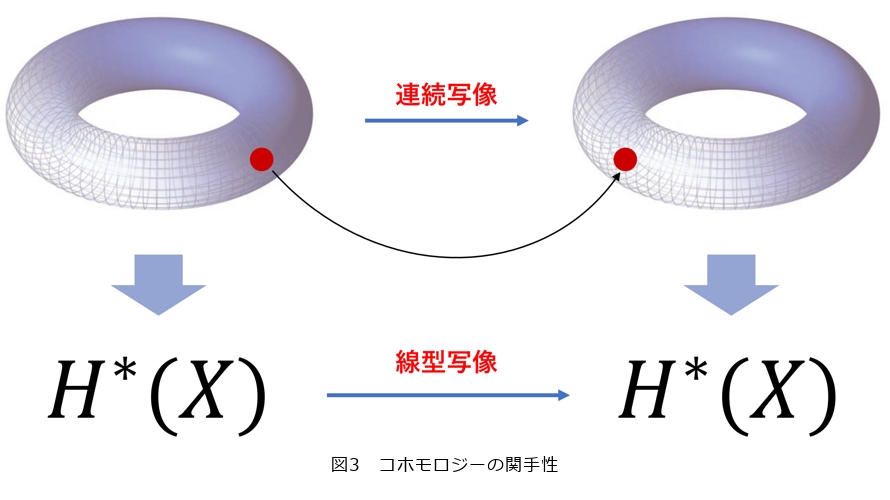
コホモロジーの関手性
セル・コホモロジーからさらに情報を取り出すためには「連続写像」を考えることが有効です(図3)。セル・コホモロジーは、連続写像*6 ![]() を逆向きの線型写像*7
を逆向きの線型写像*7 ![]() に対応させます。この性質を「関手性」と言います。一般に、「対象」に「写像(射)」の情報を付け加えたものを圏と呼び、圏の対象・射を別の圏の対象・射に写す対応規則を関手と呼びます。
に対応させます。この性質を「関手性」と言います。一般に、「対象」に「写像(射)」の情報を付け加えたものを圏と呼び、圏の対象・射を別の圏の対象・射に写す対応規則を関手と呼びます。
関手性を用いると、連続写像からデータを山ほど取り出せます。実際、どのような線型写像であっても、線型空間の基底を固定すれば行列として表せます。行列はタテヨコに数値を並べた単なる表ですから、これ自体が数値的データにほかなりません。また、行列の基本変形・行列式・固有値の計算といった線形代数の手法を駆使すれば、行列の本質的な情報を抽出することもできます。
また、関手性は図形の対称性の研究にも役立ちます。図形の対称性とは、数学的には群の連続的な作用のことです。群の連続作用が与えられると、群の要素 ![]() ごとに連続写像
ごとに連続写像 ![]() が得られ、関手性から線型写像
が得られ、関手性から線型写像 ![]() が導かれます。これは群の線型空間への作用、つまり群の表現を与えていることになります。
が導かれます。これは群の線型空間への作用、つまり群の表現を与えていることになります。
*6 連続写像:図形(位相空間)の間の写像 ![]() が連続写像であるとは、定義域の点
が連続写像であるとは、定義域の点 ![]() をわずかに変化させたとき、像
をわずかに変化させたとき、像 ![]() の変化もわずかであること。
の変化もわずかであること。
*7 逆向きの線型写像:今回の主役はコホモロジーなので扱いませんが、逆向きでないバージョンとしてセル・ホモロジーというものもあります。ホモロジーとコホモロジーは双対性によって結び付いています。
数論幾何のコホモロジー
さて、話を数論幾何に戻しましょう。数論幾何の目標は代数多様体、すなわち方程式のグラフの性質を調べることです。実数解・複素数解のグラフは連続的な図形の構造を持つため、セル・コホモロジーを使って情報を引き出すことができます。しかし、数論の本丸は整数解や有理数解といった「不連続」な数の研究です。こうした数の範囲のグラフは不連続ですから、図形の連続的な性質をとらえることに特化したセル・コホモロジーでは歯が立ちません。
この困難を乗り越えるため、数論幾何の創始者であるグロタンディークは「エタール・コホモロジー」を生み出しました。エタール・コホモロジーもまた代数多様体を線型空間に変換する不変量で、セル・コホモロジーと同様の関手性を持ちます(ただし、連続写像は「代数多様体の射」に置き換わります)。セル・コホモロジーの理論では、図形をセルという小さな(局所的な)ピースに分割し、そのつながりの情報から大域的な情報をとらえます。エタール・コホモロジーもやはり、図形や空間をいったん「局所的」なものに分解し、そのつながりの情報から「大域的」な性質を引き出します。そのために用いられるのが「層」の概念です。層は、先ほども出てきた圏と関手の理論を用いて定義される概念で、セル・コホモロジーの構成と比べると非常に抽象的で、直感的理解が難しく、理論も複雑になりがちであるという難点を持ちます。しかし、その抽象性のおかげで、通常の意味では不連続な空間の上にも疑似的に「連続性」「局所」「大域」のような幾何的な概念に意味を持たせることが可能になり、数論的な問題にも役に立つコホモロジーを生み出すことができます。
エタール・コホモロジーの理論は抽象的で複雑ですが、その分非常に強力です。リーマン予想の類似であるヴェイユ予想がエタール・コホモロジーを用いてドリーニュにより解決されたことを皮切りに、数論幾何にさまざまな応用を生み出し続けています。エタール・コホモロジーなくしては、数論幾何は成立し得なかったとさえいえるかもしれません。実際、フェルマー予想の解決にも、エタール・コホモロジーは不可欠な道具として用いられています。
現代数学は、層をはじめとする数多くの新たな概念をつくり出してきましたが、その極端な抽象性のために、簡単な物事をわざわざ難しくしようとしているように感じさせてしまうところがあります。しかしそうした抽象概念は、むしろ、「不連続な世界でも意味のある幾何学をつくりたい」といった素朴な願望や夢を実現するために、必要に迫られて生み出されたものです。かつては実態がないと思われていた負の数や複素数などの「抽象概念」が、現代の科学技術に不可欠なものとなっているように、現代数学が生み出した「役に立たない」と思われていた抽象概念も、時間とともに徐々に社会に浸透し、活用され始めています。例えば情報科学の分野では、コホモロジーがデータの構造やパターンをとらえるための強力なツールとして活用され、トポロジカルデータ解析という新たな分野を開拓し、実務に応用されています。
モチーフ──コホモロジーの親玉
エタール・コホモロジーのほかにも、用途に応じてさまざまなコホモロジーが開発されています。例えば、代数多様体の「微分幾何的な構造」を取り出すドラーム・コホモロジー、「正標数の世界の解析的な構造」を引き出すクリスタリン・コホモロジーなどです。これらは代数多様体の異なる側面に着目してつくり出されており、一見、互いに無関係です。しかし、それにもかかわらず、これらの異なるコホモロジーはいくつかの共通の性質を持ちます。さらに、さまざまな比較定理も成り立ちます。すなわち、適切な設定のもとでは、異なるコホモロジーが線型空間として同型になってしまうのです。
出自が全く異なるコホモロジーの間に、このような深い関係があるのは単なる偶然でしょうか。グロタンディークは「コホモロジーたちの背後に、その親玉に相当する対象が存在するに違いない」と考え、その仮想的な対象を「モチーフ」と名付けました(1)。
モチーフという言葉はもともと、音楽や絵画などの芸術作品を創り出す「原動力」を表す用語です。グロタンディークは、さまざまなコホモロジーを創り出す原動力、という意味でこの用語を転用したようです。そして実際にグロタンディークは、代数多様体が「射影的かつ滑らか*8」という条件を満たすという仮定のもとで「モチーフ」を実際に構成することに成功しました。これは現在では「純モチーフ」と呼ばれています(2)(3)。
*8 代数多様体のうち、通常の座標空間(アファイン空間)に無限遠を付け加えてできる射影空間の中で斉次方程式の解として得られるものを射影的な代数多様体といいます。直感的には、代数多様体上の点が無限遠まで飛んでいってもきちんと収束先があるようなもの。また、図形に自己交差や尖ったところがあると、それは特異点と呼ばれます。代数多様体が滑らかとは特異点がないことです。
混合モチーフ
しかし、グロタンディークの理論に「射影的」という条件がついているのは何とも不満足です。実際、上で出てきたコホモロジーの多くは、射影的とは限らない滑らかな代数多様体に対しても定義されているからです。そこでグロタンディーク以後、「射影的」という条件を除去してモチーフ理論を一般化する試みが行われました。その結果生まれたのが「混合モチーフ理論」です。混合モチーフ理論は、花村・レヴィン・ヴォエヴォドスキーにより独立に、異なる流儀で構成されました(3)。以下ではヴォエヴォドスキーの方法を説明します。
大雑把には、ヴォエヴォドスキーのアイデアは「セル複体への分割」に相当する操作を代数幾何の枠組みで考えるというものです。前述のとおり、方程式を実数・複素数の範囲で解いて得られるグラフをセル分割するというナイーブな方法では、数論的な情報をとらえることができません。グラフ上の点が有理数の解か否かという情報は、その点を少しでも動かしてしまうと失われてしまうためです。
ヴォエヴォドスキーがめざしたのは、整数や有理数といった不連続な世界においても役に立つ「連続変形」の概念を構築することでした。通常の連続変形では、変形パラメータ(=時間軸)として実数直線を用いますが、数論的情報をとらえるためには実数直線を使うわけにはいきません。そこでヴォエヴォドスキーは実数直線の代わりに「アファイン直線」という代数多様体を用いました。アファイン直線は、考えている数の範囲にかかわらず「1次元の座標軸」を表現する便利な代数多様体です。実数の世界では実数直線、複素数の世界では複素平面に対応します(複素平面は、実数の立場からみると2次元ですが、複素数の立場からみると1変数で表される1次元の空間です)。
ヴォエヴォドスキーはこのアイデアを精密な理論へと見事に結実させました。理論の構成から当然期待されることとして、彼の理論からはセル・コホモロジー(およびその一般化である特異コホモロジー)の代数幾何的な類似物が生み出されます。それこそが混合モチーフにほかなりません。混合モチーフには、代数多様体のさまざまなコホモロジーの情報が内在しています。例えば、特異コホモロジー、エタール・コホモロジー*9、ドラーム・コホモロジーの情報は、すべて混合モチーフから導き出すことができます。すなわち、混合モチーフはさまざまなコホモロジーの「親玉」になっているわけです。ヴォエヴォドスキーは彼自身が構築した混合モチーフ理論を用いて、コホモロジーの比較定理の一種であるミルナー予想(およびその一般化であるブロック・加藤予想)を解決し、フィールズ賞の栄誉を受けています。
*9 エタール・コホモロジー:正確には ![]() 進エタール・コホモロジー。
進エタール・コホモロジー。
モチーフのさらなる一般化へ向けて
混合モチーフのもっとも重要かつ特徴的な性質として「ホモトピー不変性」があります。通常の図形の連続変形の理論では、実数直線を変形のパラメータとして用いています。このことからほぼ自動的に、実数直線は1点に連続変形できてしまうことが従います。実際、実数直線上の点 ![]() を時刻
を時刻 ![]() で点
で点 ![]() に移す連続変形を考えれば、時刻
に移す連続変形を考えれば、時刻 ![]() では初期位置
では初期位置 ![]() にある点が、時刻
にある点が、時刻 ![]() では原点
では原点 ![]() に移動してしまうからです。
に移動してしまうからです。
混合モチーフ理論では、実数直線の代わりにアファイン直線を変形パラメータとして用いています。したがって、前述の議論と同様に、アファイン直線は1点に「連続変形」されてしまいます。これは裏を返せば、混合モチーフ理論ではアファイン直線と1点が区別されないことになります。この性質を混合モチーフの「ホモトピー不変性」と呼びます。
ホモトピー不変性は非常に強力な性質で、混合モチーフのさまざまな有用な性質を導きます。しかし一方で「混合モチーフ理論によってとらえられるコホモロジーはホモトピー不変性を満たすものに限られる」という根本的な制約も抱え込むことになります。数論幾何にはホモトピー不変性を満たさないコホモロジーが多数存在しますが、これらはすべて混合モチーフ理論の射程外となってしまうのです。
そこで筆者らは、ホモトピー不変性を「より弱い」性質に置き換えて理論全体を一から再構成することにより、混合モチーフ理論を一般化する「モジュラス付きモチーフ理論」を構築しました(4)(5)。数論幾何に現れる有用なコホモロジーの多くは、この新たなモチーフ理論で制御されることが期待されています。実際、構造層係数コホモロジー、ホッジコホモロジー、巡回コホモロジーなどの、ホモトピー不変性を満たさない代表的なコホモロジーが一般化モチーフによって制御されることが証明されています。
今後の展望
モジュラス付きモチーフ理論は、従来のモチーフ理論ではとらえられなかった幅広いクラスのコホモロジーを制御するものと期待されます。中でも、近年発達の著しい ![]() 進コホモロジーの理論の制御は重要な課題です。本稿で出現したエタール・コホモロジーは、正確には
進コホモロジーの理論の制御は重要な課題です。本稿で出現したエタール・コホモロジーは、正確には ![]() 進エタール・コホモロジーと呼ばれるものです(以下、
進エタール・コホモロジーと呼ばれるものです(以下、![]() 進コホモロジーと呼びましょう)。標語的には、
進コホモロジーと呼びましょう)。標語的には、![]() 進コホモロジーは代数多様体の位相幾何的な側面に着目するコホモロジーであり、
進コホモロジーは代数多様体の位相幾何的な側面に着目するコホモロジーであり、![]() 進コホモロジーは解析的な側面に着目するコホモロジーです。着目する性質が異なるにもかかわらず、やはり両者の間には興味深い類似や対応関係が観察されています(6)。当然、その背後には「モチーフ」が隠れているはずです。しかし、
進コホモロジーは解析的な側面に着目するコホモロジーです。着目する性質が異なるにもかかわらず、やはり両者の間には興味深い類似や対応関係が観察されています(6)。当然、その背後には「モチーフ」が隠れているはずです。しかし、![]() 進コホモロジー(の少なくとも一部)はホモトピー不変でないため、従来のモチーフ理論ではとらえることができません。しかし、モジュラス付きモチーフ理論を用いて
進コホモロジー(の少なくとも一部)はホモトピー不変でないため、従来のモチーフ理論ではとらえることができません。しかし、モジュラス付きモチーフ理論を用いて ![]() 進コホモロジーを制御できれば、従来は「類似」としてしかとらえられていなかった2つの理論を共通の土俵で比較できるようになります。
進コホモロジーを制御できれば、従来は「類似」としてしかとらえられていなかった2つの理論を共通の土俵で比較できるようになります。
新たなモチーフ理論を基盤として、不思議な類似が生み出される未知のメカニズムの解明に成功すれば、数論の研究全体に大きなインパクトを与えられると考えています。
■参考文献
(1) グロタンディーク:“数学と裸の王様 新装版: ある夢と数学の埋葬 収穫と蒔いた種と 一数学者のある過去についての省察と証言,”現代数学社,2015.
(2) https://www.math.kyoto-u.ac.jp/~tetsushi/files/hokudai200609.pdf
(3) 山崎:“モチーフ理論,”岩波数学叢書,2022.
(4) B. Kahn, H. Miyazaki, S. Saito, and T. Yamazaki:“Motives with modulus, I, II ,”Épijournal de Géométrie Algébrique, epiga:5979, 5980,2021.
(5) B. Kahn, H. Miyazaki, S. Saito, and T. Yamazaki:“Motives with modulus, III,”Ann. K-Theory,Vol. 7,No.1, pp.119-178, 2022.
(6) https://www.ipmu.jp/sites/default/files/imce/press/N35_J02_Feature.pdf

宮﨑 弘安







モチーフ理論に代表されるように、数学は「一見全く異なる対象・現象の背後に共通構造を見出し、結び付ける」力を持っています。分野の枠にとらわれることなくさまざまな領域を「つなぐ」ことが、NTT基礎数学研究センタの使命の1つです。