2021年3月号
特集
ボソニック量子計算に向けた長寿命周波数可変量子ビット
- 量子計算
- 超電導磁束量子ビット
- 3次元マイクロ波キャビティ
容量シャント型超伝導磁束量子ビットと3次元キャビティのハイブリッド化により、長寿命かつ周波数可変な3次元量子ビットを実現しました。これまで、2次元磁束量子ビットで実現されているエネルギー緩和時間は50µs程度でしたが、今回90µsまで延ばすことに成功しました。この新しいデザインは、3次元キャビティ中のマイクロ波の状態を量子ビットとして利用するボソニック量子ビットへの応用が期待できます。
Leonid V. Abdurakhimov/Imran Mahboob
樋田 啓(といだ ひらく)/角柳 孝輔(かくやなぎ こうすけ)
齊藤 志郎(さいとう しろう)
NTT物性科学基礎研究所
超伝導量子計算機
量子計算は、重ね合わせやエンタングルメント*1のように、よく研究されてはいるものの、十分に活用されてこなかった量子現象を利用した新しい計算方法です。基本素子は量子ビットと呼ばれる2準位系で、基底状態|0〉と励起状態|1〉の任意の重ね合わせ状態|ψ〉=α|0〉+β|1〉 (αとβは|α|²+|β|²=1を満たす複素振幅)を準備することができます。N個の量子ビットを用意すると、2N個の状態の重ね合わせをつくることができます。すなわち、2N個の入力を1つの量子状態として、N個の量子ビットにエンコードし、同時に演算することができるのです。この性質は量子並列性と呼ばれています。ピーター・ショアやロブ・グローバーが発見した量子アルゴリズムでは、この性質と量子位相*2の干渉効果を合わせることで、多数の入力に対する出力を効率良く得ることができます。その結果、量子計算機は、大きな数の因数分解(ショアのアルゴリズム)や大規模データ検索(グローバーのアルゴリズム)などの問題を、従来の計算機よりも格段に速く解くことができます。
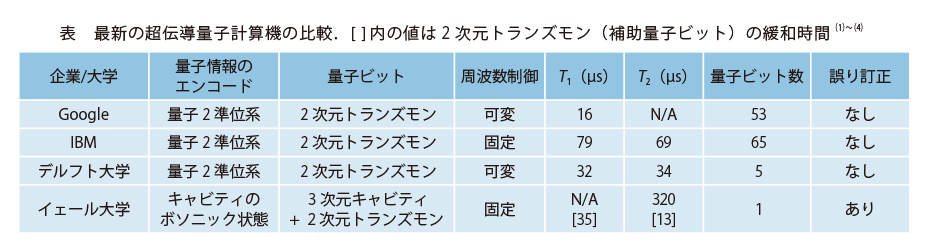
現在は量子計算機実現に向けて、超伝導量子ビット、イオントラップ、光量子ビット、スピン量子ビットなどさまざまな物理系が精力的に研究されています。それぞれの系が異なる長所と短所を持ち合わせていますが、中でも超伝導量子ビットはもっとも進んだハードウェアプラットフォームであるといえます。このことは、Google、IBM、Microsoftに代表される大企業やRigetti computingなどのスタートアップが超伝導量子計算機に注力していることからも推察されます。さまざまな種類の超伝導量子ビットが研究されていますが、大規模量子計算に向けた開発では、その制御性の良さと量子情報の保持時間の長さからトランズモン*3が主流となっています。トランズモンの中でも、量子ビットを形成する2準位間の遷移周波数が固定されたタイプと遷移周波数可変なタイプとに分かれます。一般的に前者は量子情報の保持時間が長く、後者は量子演算用のゲート操作の自由度が高いという特徴があります。表に両者の代表的な例を示します。
近年、小規模超伝導量子計算機は著しく進歩してはいるものの、汎用量子計算機の実現はいまだに挑戦的な目標となっています。最大の問題はノイズ環境との相互作用により量子情報が失われてしまうことです。量子情報の保持時間を示す性能指数は、エネルギー緩和時間*4T₁と位相緩和時間*5T₂です。Google、IBM、デルフト大学が採用しているトランズモンのT₁とT₂は最大でも100 µs程度であり(表)、量子ビットの典型的なゲート操作時間は100 ns程度です。これらの結果から、最先端の量子計算機におけるゲート操作の誤り率は10⁻³と見積もられます。この誤り率で信頼できる量子計算を実行するためには、量子誤り訂正のためのオーバヘッドが要求され、実用的な量子計算機には最低でも2千万個の量子ビット実装が必要であるといわれています(5)。現在の量子ビット実装技術を拡張していくには限界があり、分散量子計算などの次世代実装技術が期待されています。
一方、誤り耐性量子計算に対する異なるアプローチとして、hardware-efficientな量子計算方式が近年注目を集めています。この方式では、量子ビット自体が量子誤り訂正を実行する機能を有し、従来方式のようなオーバヘッドを必要としないという利点があります。有望なアプローチの1つとして、3次元キャビティ中のマイクロ波光子状態に量子情報をエンコードするボソニック量子ビットが精力的に研究されています(6)。3次元キャビティを冷却し量子現象が顕著に現れる領域に入ると、マイクロ波光子の状態はその光子数に応じて離散化された量子状態となります。すなわち、量子状態は、|0〉c、|1〉c、…|n〉c、と離散化されており、キャビティ中に0、1、2、…、n個のマイクロ波光子が存在する状態を表します。しかし、キャビティ中の光子数状態はエネルギーが等間隔に離散化されているため、|1〉cを励起すると|2〉c、|3〉c、…などの高エネルギー状態も同時に励起されてしまい、超伝導量子ビットのように任意の2準位間のみを操作することはできません。そこで、キャビティを超伝導量子ビットと相互作用させ、光子数状態のエネルギーをわずかにシフトさせることで、それぞれの光子数状態に個別にアクセスできるようにします。この量子ビットはその役割から、補助量子ビットと呼ばれていますが、ボソニック量子ビットでは非常に重要な要素となります。次に、ボソニック量子ビットのエンコーディングの例を示します。ここでは、平均光子数が等しく、偶数である|0〉L=(1/√2)(|0〉c+|4〉c)、|1〉L=|2〉cを量子ビットの2状態として用います。キャビティで生じるエラーの主要因は光子数の減少です。ボソニック量子ビットに対しては、量子状態を壊すことなく光子数の偶奇性を測定することが可能です。そこで奇数が観測された場合は光子ロスが起きたと判断し、光子を追加することでエラーを訂正できます。
本稿では、ボソニック量子ビットに適用可能な新しい周波数可変量子ビットを紹介します。この量子ビットはボソニック量子ビットの補助量子ビットとして利用できるだけではなく、ボソニック量子ビット間の可変結合素子としての応用も期待できます。可変結合素子は、大規模ボソニック量子計算機実現に向けた重要な要素技術です。
*1 エンタングルメント:量子ビット間には、古典力学では説明できないような相関を持たせることができます。このような相関あるいは状態をエンタングルメントと呼びます。
*2 量子位相:量子状態には古典的な波と同様に位相因子が存在し、量子ビット間の干渉効果を引き起こします。
*3 トランズモン:超伝導量子ビットの一種。電荷状態に量子情報をエンコードする電荷量子ビットの改良版であり、電荷量子ビットを並列キャパシタでシャントすることによりノイズ耐性を向上させ、長い緩和時間を達成しています。
*4 エネルギー緩和時間:量子ビットの励起状態が基底状態に緩和する時間。
*5 位相緩和時間:量子ビットでは、基底状態と励起状態間の量子位相の差を観測することができます。この位相差の情報が失われていく時間を位相緩和時間と呼びます。
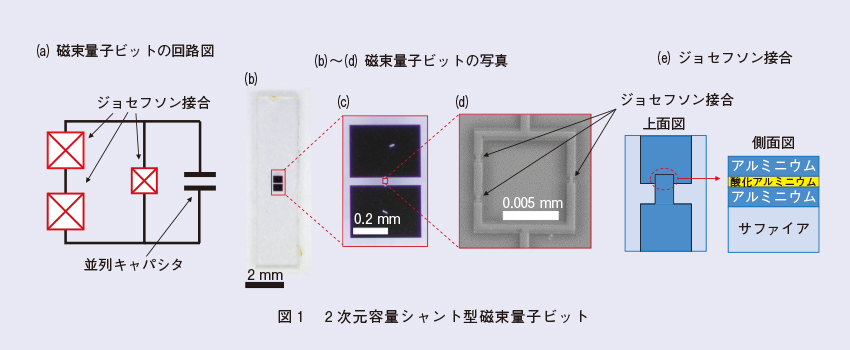
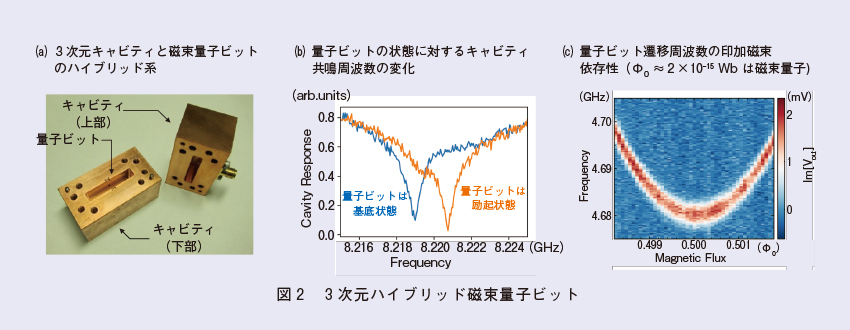
3次元ハイブリッド磁束量子ビット
容量シャント型磁束量子ビット*6は2007年に理論提案され(7)、2016年に2次元チップ上に実現されました(8)。私たちは、2次元容量シャント型磁束量子ビット(図1)を銅製の3次元キャビティ(図2(a))中に設置することで、3次元ハイブリッド磁束量子ビットを実現しました(9)。磁束量子ビットは3つのジョセフソン接合を有する超伝導ループから構成されており、接合の1つは他の2つよりも小さく設計されています(図1(a)、 (d))。この小さな接合は、2つの矩形アルミニウムパッドから成る平面キャパシタによりシャントされています(図1(a)-(c))。まず、このキャパシタをサファイア基板上に作製し、次に斜め蒸着法を用いて微小なジョセフソン接合を作製します。ジョセフソン接合は2層の超伝導アルミニウム薄膜の間に、薄い(2 nm程度)絶縁膜を挟んだ構造であり(図1(e))、酸化アルミニウムから成る絶縁膜は酸素雰囲気中でアルミニウムの表面を酸化することで形成します。
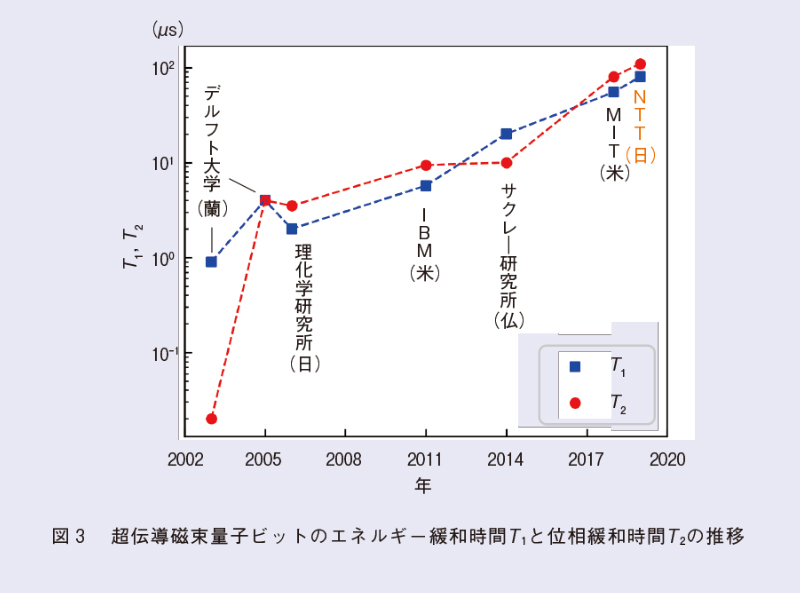
2次元容量シャント型磁束量子ビットを作製したサファイア基板を3次元共振器中に設置し(図2(a))、希釈冷凍機を用いて10 mKまで冷却します。量子ビットが基底状態から励起状態に励起されると、キャビティと量子ビットの静電結合によりキャビティの共鳴周波数が高周波側に2 MHz程度シフトします(図2(b))。つまり、キャビティの共鳴周波数を測定すると、量子ビットの状態を読み出すことができます。量子ビットの2準位間の遷移周波数は、外部磁束Φe=B∙Sによって制御可能です(図2(c))。ここで、Bは印加磁場、Sは量子ビットのループ面積を表します。Φe=0.5Φ0では、外部磁束の揺らぎに対して量子ビットの遷移周波数が安定しており(図2(c))、もっとも長い位相緩和時間が得られるため、最適動作点と呼ばれています。私たちの3次元ハイブリッド磁束量子ビットは、この最適動作点において、エネルギー緩和時間T₁=60−90 µs、位相緩和時間T₂=100 µsを記録しました(10)。これらの緩和時間は、超伝導磁束量子ビットに対する先行研究の結果を超えるものであり(図3)、周波数固定トランズモンと同程度の性能を達成しています。
*6 容量シャント型磁束量子ビット:超伝導量子ビットの一種である磁束量子ビットの改良版。磁束量子ビットは、超伝導ループを流れる電流の向き、すなわち電流がつくり出す磁束の向きに量子情報をエンコードします。容量シャント型磁束量子ビットでは、磁束量子ビットを並列キャパシタでシャントすることにより、長い緩和時間を達成しています。
ボソニック量子ビット
3次元ハイブリッド磁束量子ビットは、現在、超伝導量子計算機に広く用いられているトランズモンと同程度のエネルギー緩和時間を示すことが明らかとなりました。これは量子計算機実現に向け、トランズモンに加えて3次元磁束量子ビットも利用できることを示唆しています。3次元キャビティとの整合性の良さから、特に、ボソニック量子ビットを用いた量子計算への応用が期待できます。
3次元キャビティ中のボソニック量子ビットを用いた量子計算は、hardware-efficientな量子情報処理に向けた有望なアプローチです。最近、キャビティ中の光子数状態に量子情報をエンコードし、1量子ビットに対する量子誤り訂正の可能性が実証されました(4)。次の重要な目標は、1量子ビットに対する量子誤り訂正の精度向上に向けたプロトコル改良と、量子誤り訂正を実装した複数量子ビット間におけるゲート操作の実証です。2量子ビットゲート操作は、2つのボソニック量子ビット間を補助量子ビットで結合することにより実現可能です。例えば、2つのボソニック量子ビットを周波数固定トランズモンで結合し、制御NOTゲート操作を実証した実験が報告されています(11)。しかし、周波数固定トランズモンによるボソニック量子ビット間の結合は固定されており、量子ビット間の相互作用が必要ないアイドル状態においても常に相互作用が存在するため、エラーが蓄積する可能性があります。この問題は、可変結合素子の導入で解決することができます。3次元ハイブリッド磁束量子ビットは、外部磁場による遷移周波数の制御が可能なため、可変結合素子に適用することができます。3次元ハイブリッド磁束量子ビットを用いて、ボソニック量子ビット間の可変結合を実現するための概要を図4に示します。2つのボソニック量子ビット、すなわち2つのキャビティ間の結合は、2つの補助量子ビットを介して行われます(図4(a))。ここで、一方の補助量子ビットは容量シャント型磁束量子ビット、もう一方がトランズモンです。キャビティ間の結合のオン・オフは、図4(b)に示す補助量子ビット間のiSWAPゲートにより実現します(12)。

今後の展開
本稿では、長寿命と周波数制御性を兼ね備えた新しいタイプの3次元超伝導量子ビットを紹介しました。今後は、最近注目を集めているhardware-efficientな量子計算、すなわちボソニック量子ビットへの応用可能性を検討する予定です。
■参考文献
(1) F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Yuezhen Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis: “Quantum supremacy using a programmable superconducting processor,”Nature, Vol. 574, pp. 505-510, Oct. 2019
(2) E. J. Zhang, S. Srinivasan, N. Sundaresan, D. F. Bogorin, Y. Martin, J. B. Hertzberg, J. Timmerwilke, E. J. Pritchett, J. B. Yau, C. Wang, W. Landers, E. P. Lewandowski, A. Narasgond, S. Rosenblatt, G. A. Keefe, I. Lauer, M. B. Rothwell, D. T. McClure, O. E. Dial, J. S. Orcutt, M. Brink, and J. M. Chow: “High-fidelity superconducting quantum processors via laser-annealing of transmon qubits,”arXiv:2012.08475.
(3) M. A. Rol, F. Battistel, F. K. Malinowski, C. C. Bultink, B. M. Tarasinski, R. Vollmer, N. Haider, N. Muthusubramanian, A. Bruno, B. M. Terhal, and L. DiCarlo: “Fast, High-Fidelity Conditional-Phase Gate Exploiting Leakage Interference in Weakly Anharmonic Superconducting Qubits,”Phys. Rev. Lett., Vol. 123, No. 12, 120502, Sept. 2019.
(4) N. Ofek, A. Petrenko, R. Heeres, P. Reinhold, Z. Leghtas, B. Vlastakis, Y. Liu, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf: “Extending the lifetime of a quantum bit with error correction in superconducting circuits,”Nature, Vol. 536, pp. 441-445, August 2016.
(5) C. Gidney and M. Ekera: “How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits,”arXiv:1605.09749.
(6) W. Cai, Y. Ma, W. Wang, C. L. Zou, and L. Sun: “Bosonic quantum error correction codes in superconducting quantum circuits,”arXiv:2010.08699.
(7) J. Q. You, X. Hu, S. Ashhab, and F. Nori: “Low-decoherence flux qubit,”Phys. Rev. B, Vol.75, 140515, April 2007.
(8) F. Yan, S. Gustavsson, A. Kamal, J. Birenbaum, A. P. Sears, D. Hover, T. J. Gudmundsen, D. Rosenberg, G. Samach, S. Weber, J. L. Yoder, T. P. Orlando, J. Clarke, A. J. Kerman, and W. D. Oliver: “The flux qubit revisited to enhance coherence and reproducibility,”Nat. Commun., Vol. 7, 12964, Nov. 2016.
(9) L. V. Abdurakhimova, I. Mahboob, H. Toida, K. Kakuyanagi, and S. Saito: “A long-lived capacitively shunted flux qubit embedded in a 3D cavity,”Appl. Phys. Lett., Vol. 115, No. 26, 262601, Dec. 2019.
(10) L. V. Abdurakhimov, I. Mahboob, H. Toida, K. Kakuyanagi, Y. Matsuzaki, and S. Saito: “Driven-state relaxation of a coupled qubit-defect system in spin-locking measurements,”Phys. Rev. B, Vol. 102, No. 10, 100502(R), Sept. 2020.
(11) S. Rosenblum, Y. Y. Gao, P. Reinhold, C. Wang, C. J. Axline, L. Frunzio, S. M. Girvin, L. Jiang, M. Mirrahimi, M. H. Devoret, and R. J. Schoelkopf: “A CNOT gate between multiphoton qubits encoded in two cavities,”Nat. Commun., Vol.9, 652, Nov. 2018.
(12) R. Barends, C. M. Quintana, A. G. Petukhov, Y. Chen, D. Kafri, K. Kechedzhi, R. Collins, O. Naaman, S. Boixo, F. Arute, K. Arya, D. Buell, B. Burkett, Z. Chen, B. Chiaro, A. Dunsworth, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, T. Huang, E. Jeffrey, J. Kelly, P. V. Klimov, F. Kostritsa, D. Landhuis, E. Lucero, M. McEwen, A. Megrant, X. Mi, J. Mutus, M. Neeley, C. Neill, E. Ostby, P. Roushan, D. Sank, K. J. Satzinger, A. Vainsencher, T. White, J. Yao, P. Yeh, A. Zalcman, H. Neven, V. N. Smelyanskiy, and J. M. Martinis: “Diabatic Gates for Frequency-Tunable Superconducting Qubits, ”Phys. Rev. Lett. , Vol. 123, No.21, 210501, Nov. 2019.

(後列左から)樋田 啓/角柳 孝輔/Leonid V. Abdurakhimov
(前列左から)Imran Mahboob/齊藤 志郎






1999年に超伝導量子ビットが誕生してから約20年が経ちました。この20年で超伝導量子ビットの緩和時間は飛躍的に延びました。これからは世界トップレベルの量子ビットをさまざまな応用に活かしたいと思います。