フォノンは物質を構成する原子や格子振動の素励起です。特に、振動数が10⁴ 〜10¹¹Hzのものを超音波と呼び、エコーやソナーのような生体や水中内の観測・探査システムの信号源として古くから利用されてきました^（1）。一方、情報処理システムにおいては、超音波を含むフォノンは、デバイスの駆動過程で生じる副産物であり、正常な動作を乱す障害物としてみなされ、情報担体としての利用はこれまで積極的に試みられていませんでした。
次世代の情報担体として注目を集めるフォトン（光）も、元々は顕微鏡等の観測分野での応用にとどまっていました。その後、プラナー光波回路やフォトニック結晶などの新しいプラットフォームが登場したことで、チップスケールでの制御技術が向上した結果、現在の産業的価値が見出されました。フォノンはフォトンと同様に波動性を持ち、その挙動に類似性があります。また、同一周波数で比較すると波長が5桁も短く、さらに、自由空間への輻射がなくエネルギー損失が少ないという優れた特徴もあります^（1）。将来のIoT（Internet of Things）社会において、高周波情報処理システムのさらなる小型化、省エネ化への要請はますます高まっていくため、短波長かつ低損失なフォノンの情報担体としての活用が有望視されます。そのためには、フォトンのように、フォノンにもオンチップで多様な制御ができるプラットフォームが必要になります。

フォノンの制御プラットフォームとして、フォノニック結晶とマイクロ電気機械システム（MEMS）が古くから知られています。前者は、異なる弾性体の周期構造から成る人工音響構造で、フォトニック結晶のフォノン版になります^（1）（図1（a））。周期間隔（α）を、フォノンの波長（λ）程度にすると、構造がつくる弾性周期ポテンシャルの影響を受け、フォノンの分散関係＊1が変調されます。例えば、ブラッグ条件（nλ=2α、nは自然数）を満たす周波数近傍にはバンドギャップ＊2が発生し、波長λを持つ波は伝搬できなくなります。さらに、バンドギャップの形成により分散曲線が緩やかになり、その傾斜で決まる群速度も低下します。フォノニック結晶を用いれば、その周期構造を通して、フォノンの空間的な伝搬制御が可能になります。それゆえ、フォノニック結晶は音響工学の分野において、遮音器などの音響波制御システムの基本構造として利用されてきました。
一方、MEMSは主に半導体工学等のエレクトロニクス分野において精力的に研究されてきました。これはカンチレバーやビームのようなnm、μmスケールの立体梁構造からなり、オンチップかつ電気的に超音波振動を励起できます^（2）（図1（b））。また、梁と基板間では、振動の伝わりやすさを示す音響インピーダンス差が大きいことから、弾性振動の基板への流出が抑えられ、振動の持続時間が長い（高いQ値＊3の）共振を保持できます。近年、これら振動子において顕著に現れる非線形効果に着目した、振動の非線形ダイナミクスやそれを応用した動的制御技術に関する研究に学術的な注目が集まっています。これまでに、パラメトリック効果＊4や四波混合＊5を介した、フォノンの増幅や周波数変換といった振動の外部変調が実証されています。このように、MEMSはフォノンの動的な制御ができる一方で、局所的な構造のため、空間的な伝送はできません。対照的に、フォノニック結晶は動的な制御性はありませんが、空間的な制御性を有しています。
両者の特徴を比較すると、その機能に相補的な関係があることが分かります。私たちはこの点に注目して、2つの異なる構造を融合した「電気機械フォノニック結晶」という新しいフォノンの制御プラットフォームを提案しました^（3）、^（4）。これを用いると、フォノンのオンチップ励振や空間伝送、その動的制御を同じデバイス上で実現できるようになります。

＊1　分散関係（曲線）：波の波数と周波数間の関係性。波数は波長の逆数で、運動量と比例関係にあります。この関係から周波数に対応した波数が一意に決まり、伝搬速度などの基本的な波の伝搬特性が決定します。
＊2　バンドギャップ：波の周波数に対して分散が決まらない、つまり対応する状態が存在しない周波数帯域のことを意味します。波長と媒質の周期間隔が特定の条件（ブラッグ条件）を満たす周波数において発生します。ここでは、周期構造から強い反射を受け、波の伝搬が強く抑制されます。
＊3　Q値：共振周波数（f_res）の半値全幅（Δf_res、緩和時間の逆数）に対する比によって表される振動の質や寿命の評価に用いる無次元性能指数（Q=f_res/Δf_res）。
＊4　パラメトリック効果：周波数の異なる波が混合し、それらの和もしくは差の周波数成分を持つ新しい波が発生する現象です。MEMSの場合、外部信号により振動子内の張力を周期的に変調することで実現します。
＊5　四波混合：三次の非線形効果を介して行われる波の周波数変換法です。周波数f₁と周波数f₂の異なる2つの波を同時に入力すると、このプロセスを通して新しい周波数の波（f₃、f₄）が発生します。なお、f₃とf₄はエネルギー保存則を満たすようその値が決まります（f₁+f₂=f₃+f₄）。

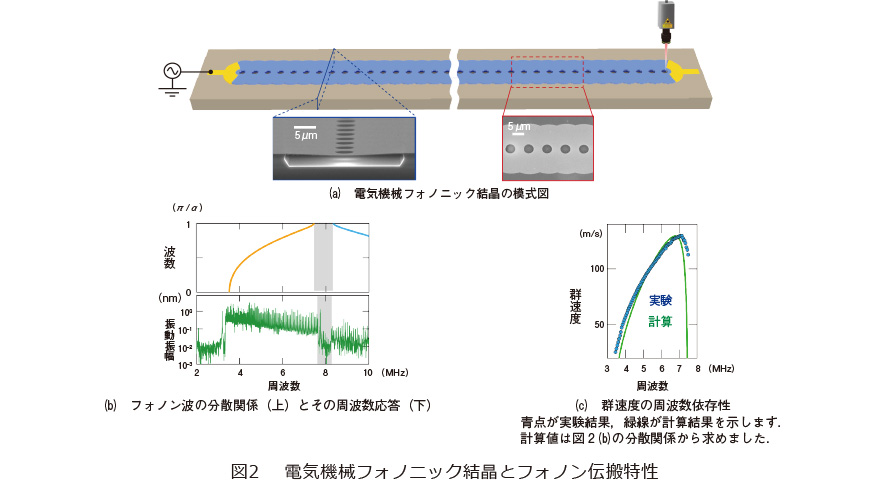
図2（a）に示すように、電気機械フォノニック結晶はガリウムヒ素（GaAs）を媒質に持つ直径22μmの円形薄膜（メンブレン）が8μmの間隔で100個一列に周期的に連結した導波路構造から構成されています^（4）。メンブレンと基板の間は中空になっており、太鼓の膜のように振動します。GaAsは圧電性＊6を有しているため、メンブレン上に設置した電極に交流電圧を加えることで、メンブレンの上下振動（超音波フォノン）を誘起することができます。この弾性振動はメンブレンの連結方向に沿って伝わっていきますが、その過程で周期孔がつくる弾性ポテンシャルの影響を受け、分散関係が変調されます。数値計算から求めた分散関係と、フォノン伝搬の周波数依存性を実際に測定した結果を図2（b）に示します。上図の分散関係では、1番目のバンド（黄色）が3.5MHzから7.4MHzにわたって形成されています。このバンドがフォノンの伝搬を促しますので、図下部の実験結果においても、導波路の一端から励起されたフォノンがその他端まで伝搬していることが確認できます。このバンドは7.4MHzで分散関係の端に到達します（波数k=π/α）、次のバンド（水色）が生じる周波数までの間に、灰色で示した空隙が生じています。これがバンドギャップです。ここではちょうどフォノンの半波長が孔間隔に一致しブラッグ条件を満たすため（λ/2=α）、フォノンは孔の位置でブラッグ反射＊7を受けます。実際に、バンドギャップの位置で、フォノン伝搬が著しく抑制されていることが分かります。また、バンドギャップにより、接する分散曲線の傾斜が緩やかになるため、フォノンの伝搬速度（群速度）が徐々に低下していくはずです。その現象を実験で確かめた結果が図2（c）です。3.5MHzから7.0MHzまでは、伝搬速度は周波数とともに増加していますが、その後は、反転して減少していることが確認できます。このことから、バンドギャップや群速度変調の発生を実験的に確認し、本構造がフォノニック結晶として機能していることが分かります。

＊6　圧電性：物体に電圧を加えると歪が生じる現象。電気機械フォノニック結晶では、この歪により、曲げモーメントが発生し、メンブレンの垂直方向に振動が発生します。
＊7　ブラッグ反射：原子が周期的に並んだ格子面に角度θで波が入射する場合、その波長（λ）と隣接する格子面間隔（α）がブラッグ条件を満たす場合（nλ=2αsinθ、nは自然数）、反射に強い干渉が現れる現象。本実験における一次元系では、θ=π/2となります。

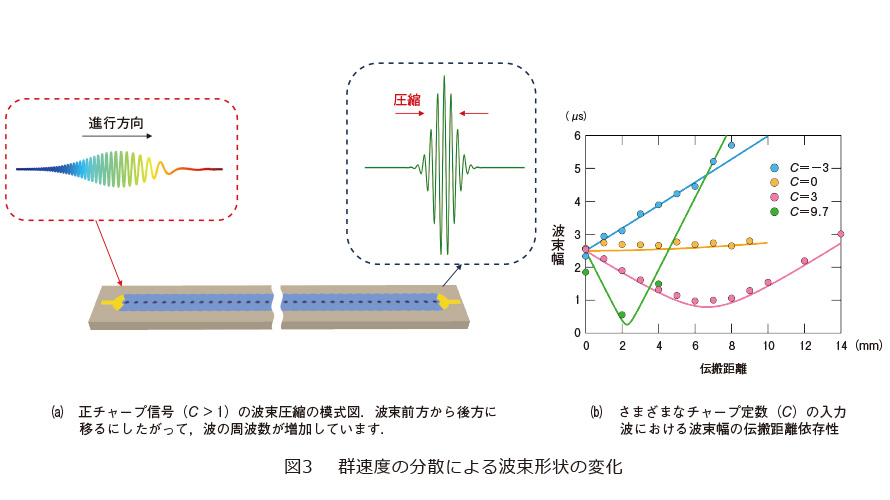
フォノニック結晶効果の実用例として、フォノンの波束制御の研究について紹介します。この導波路は、群速度分散と呼ばれる、伝搬速度が周波数によって変化する特徴を有しています。ここに、包絡線が有限の幅を持つ波束（パルス）を入力します。波束には、フォノンの振動周波数（搬送周波数）に加え、近傍の周波数成分の波も含まれています。したがって、群速度に分散がある場合、各々の周波数に応じた速度でそれぞれの周波数の波が進むため、それらを包括する波束は伝搬とともに拡がっていきます。このような波形の歪を誘起する群速度分散は、通常の導波路において望ましくない特性ですが、私たちはこれを積極的に利用し、フォノン波の圧縮や拡大といった波束制御を実現しました。
負の周波数変調（チャープ、C<0）を加えたフォノン波束を導波路の一端から加えます。ここでチャープ定数（C）の符号は、周波数が時間とともに増大、または、減少するかを決めます。搬送周波数を5.8MHzに選ぶと、この導波路では、高い周波数のフォノンのほうが低い周波数よりも速く伝搬していきます（図2（c））。負のチャープでは、入力時に高周波数の波が波束前方に低周波数の波が後方にいるので、伝搬とともに高周波数の波はより先に進み、低周波数のそれはさらに遅れるため、結果的に波束は拡大していきます。反対に、正のチャープを入力すると、今度は波束前方に低周波数、後方に高周波数の波が偏在していることになりますので、同じメカニズムでも、この場合は伝搬とともに波束が圧縮していきます（図3（a））。図3（b）はこれを実験的に確かめた結果です。ここでは、さまざまなチャープ定数（C）で入力した波束幅の伝搬距離依存性をプロットしています。前述のとおり、C=−3の負のチャープ入力では、波束幅が距離に比例して増加している一方で、C=3の正チャープ入力では波束幅が減少していることが分かります。しかし、距離7mmを超えると波束の変化が、一転、圧縮から拡大へと転じています。これは、入力時のチャープによる波の偏在が解消されたためと理解できます。また、周波数掃引範囲を広げると、この圧縮効果も強くなります。実験では、C=3から9.7へ増やしたところ、波束幅が2μsから測定装置の分解限界値である0.6μsまで圧縮しました。このように、フォノニック結晶の特異な分散関係を用いて、伝搬フォノンの波束形状を制御することができます。この実験では入力にチャープ信号を使いましたが、後述する非線形効果を合わせて用いれば、無変調の入力信号からフォノン波束の圧縮・拡大を実現することも可能です^（5）。

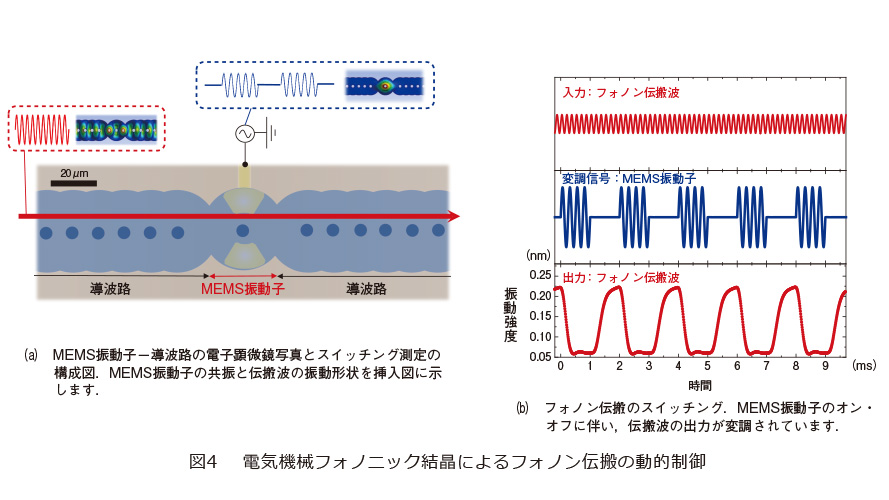
電気機械フォノニック結晶が持つMEMSの特性を活用すれば、フォノン波の動的制御も可能です^（3）。ここでは、導波路の中央に設置したメンブレン振動子を外部変調用ノードとして使います（図4（a））。このメンブレンは隣接するメンブレンとの結合が弱いため、3MHz以下の低周波数領域では単一のMEMS共振器として振る舞います。それゆえ、表面に設置した電極から交流電圧を加えることで、導波路の伝搬モードから、スペクトル的に独立し、振動がメンブレン内に局在した共振を励起できます。これを強く励起すると、大きな振動振幅によりメンブレン内の応力分布が再調整されます。その結果、中央のメンブレン振動子を通過する導波路のフォノン波もこの弾性特性の変化から影響を受け、伝搬スペクトルが変調します。伝搬波の振動周波数を適切に調整すれば、フォノンの伝搬強度が低下することになります。それを実験的に確かめた結果が図4（b）になります。ここでは、5.745MHzの伝搬波を連続波として導波路端から加え、同時に、メンブレン振動子から1.855MHzの共振を1.0msの間隔で周期的に加えたときの、伝搬波の他端での振動強度を時間領域で測定しています。確かに、中央のメンブレンが振動しているときだけ、伝搬強度が低下していることが分かります。このように、外部から変調信号を電気機械フォノニック結晶に加えることで、フォノン波伝搬の動的な制御が可能になります。
本稿では説明を割愛しましたが、このほか、振動エネルギー転送や全機械ランダムアクセスメモリ操作、さらに、フォノン伝搬波の周波数変換も、MEMSの非線形効果を用いて成功しています。

電気機械フォノニック結晶を基盤にすれば、オンチップで空間的かつ動的なフォノン制御を実現できます。しかし、その動作周波数は数MHzと低く、実用性を追求するためには、極超音波と呼ばれるGHz帯まで周波数を引き上げる必要があります。私たちは、最近、この極超音波デバイスの作製にも成功しました^（6）。また、マグノンと呼ばれる強磁性スピン波を活用した極超音波フォノンの動的制御の研究にも取り組んでいます。本稿で説明した電気機械フォノニック結晶のフォノン制御技術と組み合わせることで、高周波で動作するフォノニック能動素子やそれらを集積したフォノン波回路の構築が可能となり、情報担体としてのフォノンの有用性が飛躍的に高まると私たちは期待しています。

■参考文献
（1）　M. Maldovan：“Sound and heat revolutions in phononics，”Nature，Vol．503, pp．209-217，2013.
（2）　K. L. Ekinci and M. L. Roukes：“Nanoelectromechanical systems,”Review of Scientific Instruments, Vol.76, No.6, June 2005.
（3）　D. Hatanaka, I. Mahboob, K. Onomitsu, and H. Yamaguchi：“Phonon waveguides for electromechanical circuits,” Nature Nanotechnology, Vol.9，No.7，pp．520-524，July 2014.
（4）　M. Kurosu, D. Hatanaka, K. Onomitsu, and H. Yamaguchi：“On-chip temporal focusing of elastic waves in a phononic crystal waveguide,” Nature Communications, Vol.9，No.1331，2018.
（5）　M. Kurosu, D. Hatanaka, and H. Yamaguchi：“Mechanical Kerr Nonlinearity of Wave Propagation in an On-Chip Nanoelectromechanical Waveguide,” Phys. Rev. Applied 13, 014056，Jan. 2020.
（6）　D. Hatanaka and H. Yamaguchi：“Real-Space Characterization of Cavity-Coupled Waveguide Systems in Hypersonic Phononic Crystals,” Phys. Rev. Applied 13, 024005，Sept．2020.