カオスという言葉をネットで検索すると、「無秩序で、さまざまな要素が入り乱れ、一貫性が見出せない、ごちゃごちゃした状況・様相を形容する表現」とされています。「今の株価の動きはカオス的だ」とか「私の机の上はまさにカオスだ」など、予測のつかない不規則な状態が一般にカオスと呼ばれているようです。一方、数学の世界でカオスというと、こちらは学問の対象として具体的に性質が規定されているようです。数学的に厳密な表現ではありませんが、分かりやすく書くと「一見無秩序にみえる複雑な動きでありながら、決まった法則に従って時間変化をする再現性のある振る舞い」という表現ができるかと思います。不規則でランダムな動きと、規則性を持つ周期的な動きのちょうど中間的な振る舞いとして、数学や物理学の対象として注目を集めてきたわけです^（1）。
カオスには、いくつかの特徴があります。まず、同じ初期条件でスタートしたら、その後は同じ振る舞いを示すという「規則性・再現性」があるという点で、これはランダムな動きとは一線を画す重要な性質です。したがって、最初の状態が把握できれば、原理的にはその後の動きを完全に予測できることになります。しかし、カオスには、ほんの少しの初期条件の違いが大きな変化を引き起こす「バタフライ効果」という性質があり、これにより実際には将来予測が極めて困難になるという特徴も持っています。最初の状態が完全に把握できれば、原理的にはその後をすべて予測できるわけですが、最初の状態がほんのちょっと、例えば0.01％違うだけでも、しばらく時間が経ったのちの振る舞いが大きく異なってしまうわけです。これは例えば、ラグビーボールを平らな床の上に落としたときを想像すると分かりやすいかもしれません。ラグビーボールの動きはあくまで物理の法則に忠実に従っているわけで、もし完全に同じ条件で床の上に落とすことができれば、その後の運動も繰り返し再現できるはずです。しかし、実際にはほんの少しだけ落とす角度や速度が違うわけで、それにより、その後の振る舞いは全く変わってしまいます。
このような複雑な振る舞いが、非常に簡単な力学系において発生することもカオスの特徴です。そういう意味では、例えば、天気の振る舞いは、気温、湿度、風向、風速、気圧等、非常に複雑な系に依存しており、実際にはカオスと呼べないということになります。しかし、例えば3つの星がお互いの重力で引き合う「三体問題」では、カオス運動が起きることが知られています。3つの星と重力という極めて簡単な力学系であるにもかかわらず、複雑な振る舞いがみられる点がカオス現象の興味深いところです。
このように、カオスは複雑で取り扱いが難しそうな現象なので、従来はむしろ制御不能で技術応用は難しいと考えられてきました。しかし、カオスの複雑さをむしろ積極的に利用し、情報の暗号化を行う秘匿通信や、カオスが生成される直前の「カオスの縁」状態を用いた高効率の機械学習＊1など、カオスを技術応用しようという試みが現在進められています^（2）。ただ、前述したように、カオスは初期条件の変化に対して極めて敏感なので、いかにして安定にカオスを生成できるかが、カオスの応用を考えるうえでの大きな技術課題であるといえます。このような背景のもと、私たちはナノメカニカル振動の非線形性を用いることにより、外部から安定にカオス発生の制御が行える新しいカオスの生成手法を提案することに成功しました^（3）、^（4）。以降ではその手法について、概略を述べます。

＊1　機械学習とカオスの縁：機械学習とは人工知能を構成する技術の1つです。コンピュータにより大規模データから共通のパターンやルールを見つけ出し、それを新しい入力データに適用することにより、さまざまな判断や結果の予測を可能とする技術です。機械学習にもさまざまな手法が存在しますが、データ処理を行うネットワーク自体を学習させるディープラーニングなどの手法とは異なり、固定されたネットワークからの出力の重み付けだけを学習させることにより機械学習を実現するリザバー計算の手法が、最近注目を集めています。リザバー計算ではカオス状態が発生する近傍の「カオスの縁」状態を用いることにより特性の優れた計算ができる可能性が指摘されています。

高感度センサや高周波フィルタ、プロジェクタなどさまざまな機器応用が行われているMEMS（Micro Electro Mechanical Systems）は、微細構造の機械的な「動き」を使って動作させる素子を、チップ上に集積化させたものです。このMEMS技術におけるメカニカル振動子＊2を用いたカオス発生手法の研究は、MEMSによるセンサ部と機械学習を行う信号処理部の集積化など、応用上の重要性が着目されていました。しかし、メカニカル振動子を用いたカオス生成について成功した例はあったものの、応用上の研究はあまり進んでいませんでした。その大きな理由の1つは、メカニカル振動子を用いたカオス発生には櫛型電極などの複雑な素子構造が必要であり、また数10ボルトという高電圧が不可欠であったことにあります。今回、NTTの研究所ではナノメカニカル振動子の「秤動＊3」運動に着目し、2つの異なる高周波信号を入力するだけという、極めて簡便な方法でカオス信号を発生させる手法を実証し、素子の小型化と低電圧駆動を実現しました。
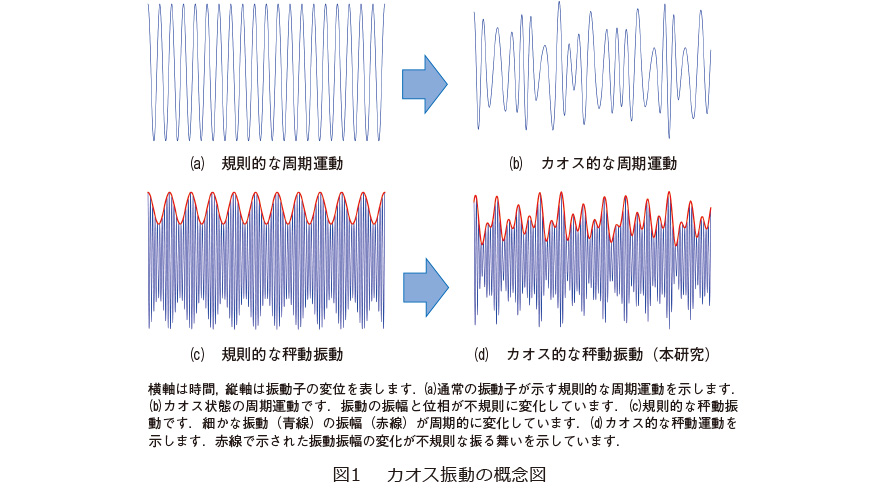
図1に振動子によるカオス生成の様子を示します。通常の振動子は規則正しい周期運動（図1（a））を行いますが、ある条件の下ではこの周期運動が乱れ、カオス振動になります（図1（b））。このカオス振動をつくり出すには振動子の非線形性を活用する必要があり、メカニカル振動子で実現するには、櫛型電極と呼ばれる大きな構造と、数10ボルトという高い電圧を加える必要がありました。これに対し、私たちの研究では振動子の「秤動」振動を用いることにより、この問題を解決しました。秤動とは、一般に天体の運動に対して使われる言葉で、例えば月が地球の周りを公転する際、本来の27.3日の公転周期に加え、もっと長い周期の運動を、その公転軌道の周りで行っていることが知られています。これが秤動運動にあたりますが、振動子の場合には、ある決まった周波数の振動において、その振幅が周期的に変化した図1（c）のような振る舞いが秤動運動になります。ちょうど、AMラジオに使われている振幅変調（AM: Amplitude Modulation）された波と同じ振る舞いです。私たちは、この振幅の変化が、ある条件ではカオスとみなされるかたち（図1（d）の赤線）で起きることを初めて見出し、それをナノメカニカル振動子で実現することに成功しました。
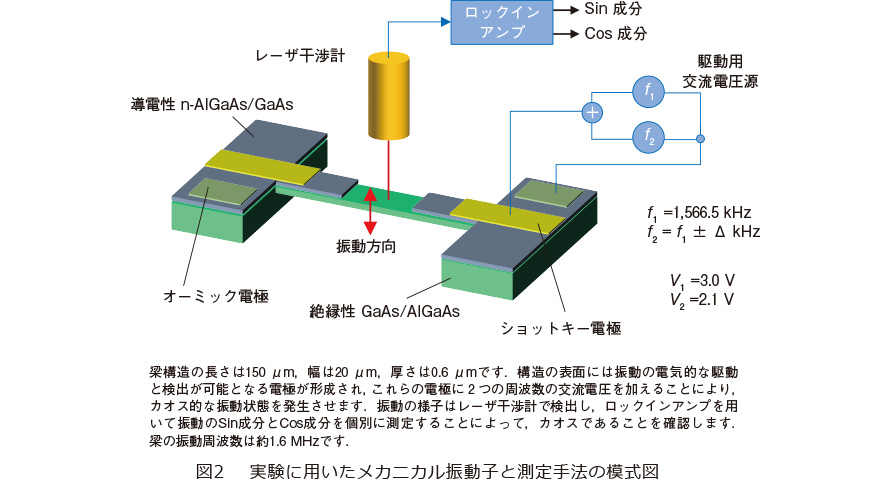
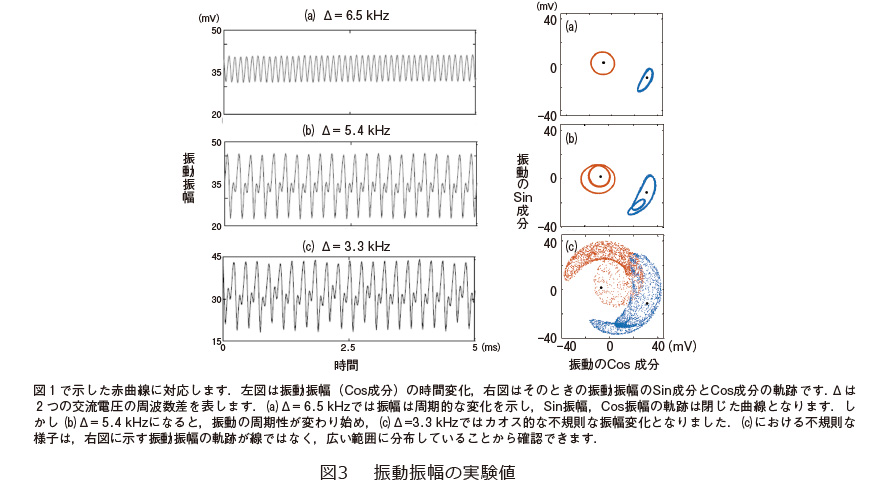
図2に実験に用いた装置を示します。「両持ち梁構造」は圧電半導体であるガリウムヒ素（GaAs）とアルミニウムガリウムヒ素（AlGaAs）の接合構造から作製されており、赤矢印の方向に振動します。この電極に交流電圧を加えることによって梁の振動を引き起こし、その動きをレーザ干渉計で計測します。測定された振動の振幅はロックインアンプを用いてSin成分とCos成分に分けて記録します。秤動振動を引き起こす手法は非常にシンプルで、振動子を駆動するのに2つの異なる周波数（図中のf₁とf₂）の交流電圧を加えるだけです。2つの異なる周波数が合わさると、それらが干渉して「うなり」を打つことはよく知られています。このうなりが振幅変調、すなわち秤動運動を引き起こすわけですが、その周波数と振幅をうまく選んでやるとカオスの生成が可能になります。図3に得られた振動の様子を示します。2つの駆動周波数の差が3.3kHzになると振動の振幅と位相がランダムに変化し、カオスとしての振る舞いを示していることが分かります。
さて、カオスであることを確認するにはLyapunov指数＊4と呼ばれる値を計算し、前述した「ほんの少しの初期条件の違いが大きな変化を生み出す」という性質を、定量的に確認する必要があります。私たちは東京工業大学との共同研究により、数値計算を用いて実際にそのような性質がみられることを確認しました。
この手法には3つの大きな利点があります。第1に、数ボルト（実験では2〜3V）という小さな電圧で駆動でき、カオスの発生を電気的に自在に制御できるという点です。このため、現在のエレクトロニクス技術と整合させることが容易です。第2に、櫛型電極のような大きな構造を必要としないため、微細化・集積化が可能です。MEMSのマイクロフォンやセンサなどと集積化し、マイクで収音した信号をオンチップで機械学習させて処理することができるかもしれません。さらに第3の利点は、このようなメカニカル振動子に限らず、さまざまな物理系の振動子に対しても応用可能であるという点です。例えばレーザに用いられている光共振器など、より広い範囲の通信技術に応用し、秘匿通信や光を用いた機械学習などに応用できるのではないかと考えています。

＊2　メカニカル振動子（機械振動子）：弾性変形を周期的に繰り返すことにより機械的な振動が継続する人工構造体。鐘や鉄琴など楽器の振動板もメカニカル振動子の一種です。最近では微細加工技術の発展に伴い、髪の毛よりも小さなメカニカル振動子を半導体チップに集積することも可能になっており、MEMS振動子として実用化が進められています。メカニカル振動子のもっとも代表的な形状の1つは本研究でも用いられている両持ち梁と呼ばれるもので、橋や鉄琴の振動板に類似した形状をしています。
＊3　秤動：月や地球などの天体は自転や公転という決まった周期運動を行っていますが、この運動とともに、ゆっくりとした別の周期運動も行っています。このような運動は「秤動」と呼ばれ、自転や公転に比較して小さく、また周期も数年から数万年という大きなものであり、潮の満ち引きや他の惑星の引力など、さまざまな要因により引き起こされます。メカニカル振動子はある決まった周波数で規則的な振動運動を行いますが、振動子が持つ非線形性により完全な周期運動にはならず、長い周期の振幅変化を伴います。この振幅変化は天体の秤動運動に相当するものといえますが、通常は天体と同様に非常に小さな変化しかみられません。しかし、秤動運動の周波数に相当する周期的な外力が加わると、共鳴現象により大きな秤動運動が引き起こされます。今回の研究では、外部より2つの振動数を加え、その差周波を秤動運動に共鳴させることにより、カオス信号を発生させることに成功しました。
＊4　Lyapunov指数：カオス的な力学系では、ほんの少しだけ異なる初期条件でスタートしても、力学系を表す座標（例えば振動子の変位）が時間とともに大きく異なっていくことが、不規則で複雑な振る舞いを引き起こす原因です。これを数学的に表す指標として、2つの運動の座標間の距離が時間に対してどのように指数関数的に増大していくかを示す指数をLyapunov指数と呼びます。カオスであるためにはLyapunov指数が正であることを確認する必要があります。

本稿ではナノメカニカル振動子における秤動運動を用いた新しいカオス信号発生手法について、ごく簡単に解説しました。この手法では、従来手法に比較して、桁違いに小さい電圧でカオスの発生を駆動することが可能で、また大きな電極構造を用いないため小型化、集積化に適した素子を実現することができます。一方、図1からも理解できるように、秤動運動によるカオス信号は、もともとの振動に比較して、ずっと周波数が低いため、実用的な周波数のカオス信号を生成するためには、より高い周波数の振動子が必要です。私たちは最近フォノニック結晶を使ってGHzに至る周波数の振動子を作製することにも成功しており、このような高周波化は、今後進めていかなければならない重要な目標となっています。このような方向にも今後チャレンジを進め、機械学習等への応用を実現していきたいと考えています。

■参考文献
（1）　山口：“カオスとフラクタル，”筑摩書房, 2010．
（2）　中野：“小特集　リザバーコンピューティング，”電子情報通信学会誌, Vol.102，No.2, 2018．
（3）　https://journal.ntt.co.jp/article/10464
（4）　S. Houri, M. Asano, H. Yamaguchi, N. Yoshimura, Y. Koike, and L. Minati: “Generic Rotating-Frame-Based Approach to Chaos Generation in Nonlinear Micro- and Nanoelectromechanical System Resonators,” Phys. Rev. Lett.，Vol．125，No．17, 174301，Oct．2020