超伝導量子回路＊1は、その回路設計の自由度を活かして、基礎から応用まで幅広く研究されています。まずは、基礎研究の例を紹介します。超伝導量子回路研究の原点は、「ミクロな世界で成立する量子力学は、どこまでマクロな系に適用可能か」という根本的な疑問にあります。NTTではこの疑問に答えるために超伝導磁束量子ビット＊2を用いた実験を行い、量子ビットのループを、1秒間に1兆個もの電子が時計回りに流れる電流状態と反時計回りに流れる電流状態の量子重ね合わせが実現することを実証しました^（1）。その結果、電子や原子のようなミクロな系だけではなく、µm程度のマクロな人工構造においても量子力学が成立すること示しました。次に、情報通信研究機構との共同研究により、回路設計を工夫することで、通常の原子と光の結合では到達することのできないような強結合を実現し、共振器量子電磁力学＊3の新しい領域を探索することが可能となりました。ここでは、超伝導人工原子（超伝導磁束量子ビット）とマイクロ波光子を用いて、それぞれのエネルギーよりも両者の結合エネルギーのほうが大きくなる深強結合領域を実現し、これまでにない物理現象を観測しました^（2）。
このように基礎物理研究において新境地を開拓してきた超伝導量子回路ですが、その応用もさかんに研究されています。もっとも有名な例は、Google、IBM、中国科学技術大学、理化学研究所などが開発を手掛けている超伝導量子コンピュータです。ここで利用される超伝導量子回路はトランズモンと呼ばれる量子ビットです。トランズモンは外部磁場に対して遷移周波数がほとんど変化しないため、コヒーレンス時間＊4が長く、量子コンピュータの構成要素に適しています。一方、超伝導磁束量子ビットは外部磁場に対して遷移周波数が大きく変化するため、磁場センサへの応用が期待されています。また、遷移周波数の制御性を利用して、D-Waveや産業技術総合研究所などでは量子アニーラ＊5への応用も進められています。
本稿では、量子センサの例として磁束量子ビットをベースにした局所電子スピン検出とハイブリッド温度計を紹介します。さらに、トランズモンを補助量子ビットとして用いる新しいタイプの量子ビット（ボソニック量子ビット）の展望を述べます。

＊1　超伝導量子回路：量子力学で記述される回路素子を含む超伝導回路。超伝導量子回路を構成する回路素子としてはジョセフソン接合、インダクタ、キャパシタなどが挙げられます。ジョセフソン接合は極めて薄い絶縁膜を2つの超伝導体で挟んだ構造。超伝導体の位相に対して非線形な超伝導電流が流れるため、超伝導量子回路における非線形素子として利用されます。超伝導量子ビットにおいては、超伝導体としてアルミニウム、絶縁膜として酸化アルミニウムが多く利用されます。
＊2　超伝導磁束量子ビット：複数のジョセフソン接合を含む超伝導ループで構成される超伝導回路で、適切な磁場バイアスをかけることで時計回りの電流状態と反時計回りの電流状態の2つの状態を量子2準位系として扱うことができます。
＊3 共振器量子電磁力学：共振器中に閉じ込められた光と原子の相互作用を記述する量子論。超伝導量子回路からなる人工原子と共振器中のマイクロ波が相互作用する系を記述する場合は、回路量子電磁力学と呼ばれることもあります。
＊4 コヒーレンス時間：量子ビットが量子情報を保持することのできる時間。
＊5 量子アニーラ：規模が大きくなると現在のコンピュータでは解くことの難しい最適化問題を量子力学の性質を利用して解く装置。

超伝導磁束量子ビットは、量子準位間の遷移周波数を測定することにより、ループを貫く磁場の変化を高感度に検出することができます。後述のように、この磁場センサは、少数の電子スピンがつくり出す磁場を検出する感度を有しています。さらに、磁束量子ビットのループサイズは数µm程度であり、高空間分解能な磁場測定も可能です。そこで、NTTでは高感度・高空間分解能な電子スピン共鳴（Electron Spin Resonance：ESR）測定装置の研究を開始しました。
ESRは、物質中でペアを組まない電子（不対電子）の情報を得ることができるため、材料探索、物性評価、創薬、医療分野において不可欠な分析手法です。通常のESRでは、体積が数mL程度のスピン試料を空洞共振器（キャビティ）中に設置し、キャビティの共振周波数でのマイクロ波応答を測定します。キャビティと電子スピン1個の相互作用が弱いため、この手法によりESR信号を観測するためには、試料中に10¹³個程度の電子スピンが含まれている必要があります。また、ESR信号はスピン試料全体を平均化したものとなり、局所的な情報を得ることはできません。
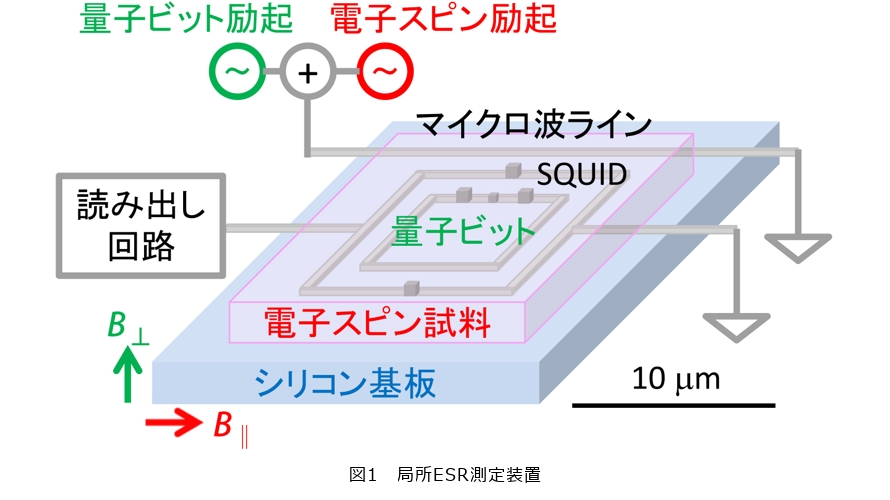
一方、超伝導量子回路を用いた局所ESR測定装置は、磁束量子ビットや超伝導量子干渉計〔Superconducting QUantum Interference Device：SQUID（SQ）〕などの「センサ」とその情報を取り出す「読み出し回路」から構成されています（図1）。電子スピン試料にマイクロ波を照射すると、スピンがつくり出す磁場が変化し、この変化をセンサが検出します。ここでは、センサ制御用のµT程度の磁場B_⊥と電子スピン偏極用のmT程度の磁場B_‖を印加しています。電子スピン検出に共振器を使わず、広帯域なマイクロ波ラインからマイクロ波を照射するため、測定可能な周波数領域に制限がありません。すなわち、周波数と磁場B_‖を掃引しながら広いパラメータ領域でESRスペクトルを測定することができ、測定対象からより多くの情報を得ることが可能です^（3）。
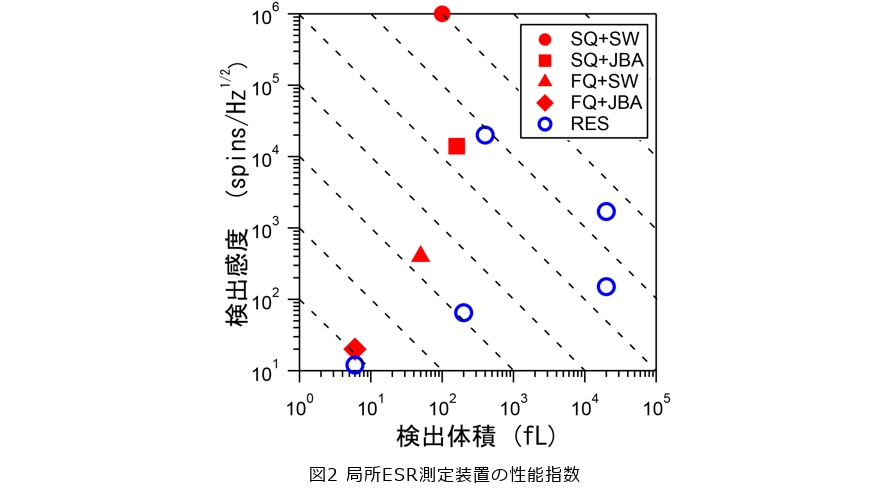
次に、局所ESR測定の性能指数向上に向けたこれまでの取り組みを紹介します。本研究開始当初は、磁場センサとしてSQを用い、読み出し回路にSQのスイッチング読み出し回路（SW）を適用することにより、光学結晶（Y₂SiO₅）中のエルビウムに由来する電子スピンを感度10⁶スピン/√Hzで検出することに成功しました^（4）。その後、磁場センサ部分をSQから磁束量子ビット（Flux Qubit：FQ）に置き換え、読み出し回路をSWからジョセフソン分岐増幅器＊6のスイッチング読み出し回路（JBA）に変えることで感度が約5桁改善し、20スピン/√Hzを達成しました^（5）。また、検出体積は、磁場センサ部分のループサイズを小さくすることで、150fLから6fLまで低減することに成功しました。これらの結果を、他研究グループの2次元超伝導共振器（RES）を用いたセンサの性能指数とともに図2に示します。

＊6　ジョセフソン分岐増幅器：ジョセフソン接合を含む共振器は、接合の非線形性のために双安定状態を示します。この状態を利用し、微小な信号を増幅するデバイスをジョセフソン分岐増幅器と呼びます。磁束量子ビットを読み出す際は、量子ビットの状態に応じて共振器の終状態が異なることを利用します。SQUIDのスイッチングを用いた読み出し回路と異なり、ジョセフソン分岐増幅器を用いた読み出し回路では、共振器の終状態が電圧を発生しないため、発熱を抑えるための冷却時間を必要としません。その結果、短い周期での繰り返し測定が可能となり、平均化により信号の精度が向上します。

ナノダイヤモンド中の電子スピン集団を温度計として利用し、磁束量子ビットを電子スピン検出器として利用することで、超小型温度計を実現し（図3）、極低温における温度を精密に測定することに成功しました^（6）。
小型の温度センサは熱容量が小さく被測定系から温度計に流れ込む熱量が小さいため、応答速度が速く、被測定系への影響を抑えた測定が可能です。また、温度測定の空間分解能を上げることができるので、微小領域の温度の空間分布を測定するような新たな応用も期待されます。しかし、温度センサの小型化と高感度化の両立は難しいことが知られています。なぜならば、温度センシングでは温度計を構成する物質の物理量の温度変化を測定しますが、温度計を小型化すると物質の量が減り、測定感度が低下するためです。この問題を解決するために、磁束量子ビットとナノダイヤモンド中の常磁性スピンを結合させたハイブリット系による量子センシングを実現しました（図3）。
ナノダイヤモンド中にはNV中心＊7やP1中心＊8をはじめとしたさまざまな種類の欠陥が存在し電子が束縛されています。この電子はスピンを持ち、外部から磁場を印加するとスピン状態に応じてエネルギーが変化するゼーマン分裂が生じます。電子スピン系のエネルギー準位は磁場に加えて、原子核スピンとの超微細相互作用やスピンが1以上の場合に現れる磁気異方性のエネルギーによって決まります。熱平衡状態になるとそれぞれのスピン状態の占有率は温度とエネルギーによって決まるため、ナノダイヤモンドは温度に依存した磁化を生じます。この磁化の変化が、磁束量子ビットを貫く磁束の変化として測定されます（図3）。磁束量子ビットの磁場感度を温度感度に換算した結果、希釈冷凍機の最低温度9.1mKにおいて、1.3 µK/√Hzという高感度な性能指数が確認されました。
各種温度計の性能指数を比較すると（図4）、本成果が小型かつ高感度な温度計を実現していることが分かります。一般的に利用されている抵抗温度計は、全温度領域において温度計を校正する必要がありますが、本温度計は、測定している磁化の温度変化が理論的に予測できるため、ある1点の温度において校正するだけで全温度領域を測定することができます。小型の温度計としては単一量子ドットを用いたセンサもありますが、本温度計は格子温度の測定ができるという利点があります。また、本温度計で測定可能な温度は極低温ですが、温度計の自己発熱や大きな熱容量による応答の遅さ等のために正確な温度測定が難しい極低温下での温度測定に新たな技術として貢献すると期待されます。

＊7　NV中心：ダイヤモンド中の炭素を窒素が置換し、その窒素と、炭素が欠損した空孔とが隣り合った複合欠陥をNV中心と呼びます。ダイヤモンドにピンク色に近い色を生じさせる色中心です。
＊8　P1中心：ダイヤモンド中の炭素を窒素が置換した欠陥をP1中心と呼びます。ダイヤモンドが黄色味を帯びる原因となる色中心です。

超伝導量子コンピュータの研究開発は、2019年にGoogleから53量子ビットプロセッサが従来のスーパーコンピュータを上回ったとする「量子優位性の実証」の発表があり^（7）、2022年には、IBMが433量子ビットプロセッサを発表するなど、日進月歩で進展しています。しかしながら、実用的な誤り耐性型汎用量子コンピュータを実現するには膨大な数の量子ビットが必要とされています。これは、量子ビットが外部ノイズに弱くエラーが頻繁に発生するため、量子誤り訂正用に冗長な量子ビットが必要になるためです。例えば、2048ビットの数を因数分解するために2000万個の量子ビットが必要という試算があります^（8）。現在のデザインでは、チップ上に配置可能な量子ビット数は1000個程度であり、それ以上はチップ間配線等の新しい技術が必要となります。また、膨大な数の量子ビットを制御するための高周波配線や冷凍機技術にもブレークスルーが必要となります。
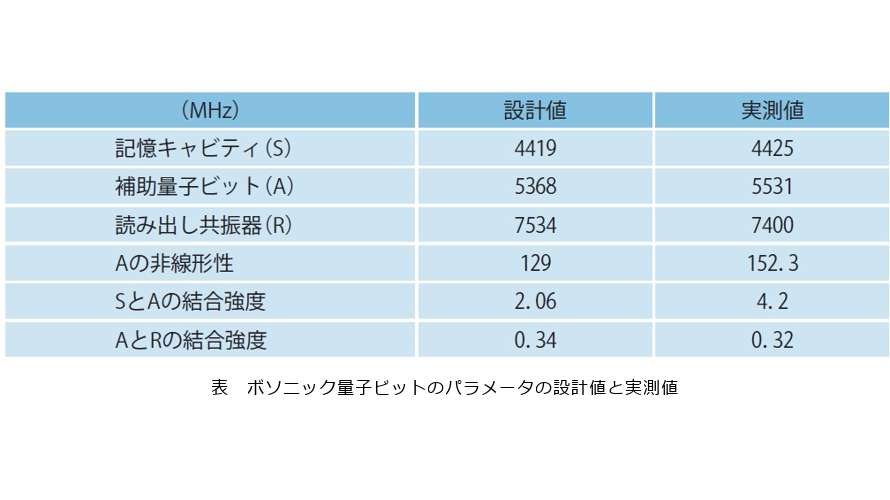
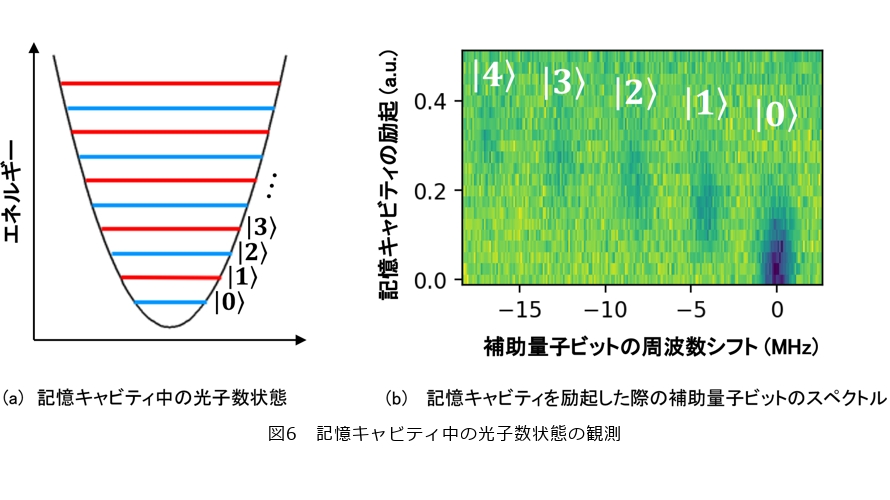
この量子ビット数の問題を解決し得る技術として注目されているのがボソニック量子ビットです。ボソニック量子ビットでは、超伝導キャビティ中の原則、無限にあるエネルギー準位に量子情報をエンコードすることにより、その冗長性を利用して量子エラー訂正を行います。記憶キャビティ中に複雑な量子状態を準備するために、トランズモンを補助量子ビットとして利用します。さらにトランズモンの状態を読み出すための共振器も必要です。ボソニック量子ビットの構成要素を図5に示します。各構成要素（記憶キャビティ、補助量子ビット、読み出し共振器）の周波数と要素間の結合強度を注意深く設計し（表）、記憶キャビティ中の光子数状態＊9を識別することに成功しました（図6）。この結果は、各光子数状態にアクセスし、複雑な量子状態を準備するための第一歩となります。今後、記憶キャビティ中にボソニック量子ビットをエンコードしていく予定です。

＊9　光子数状態：キャビティ中にマイクロ波光子がn個存在する状態を光子数状態と呼び、|n〉と表します。マイクロ波で記憶キャビティを励起すると、コヒーレント状態と呼ばれる光子数状態の重ね合わせ状態が現れ、単一の光子数状態を準備することはできません。光子数状態を準備するためには、補助量子ビットの非線形性が必要となります。

本稿では、高度に発展した超伝導量子回路の量子情報技術への応用として、局所ESR測定装置、超小型温度計、およびボソニック量子ビットを紹介しました。
局所ESR測定装置においては、長寿命磁束量子ビット^（9）や量子電磁力学を応用した読み出し回路を用いて、さらなる感度向上を進め、単一電子スピン検出感度をめざします。測定対象に関しても、固体電子スピン試料に限らず、ニューロンや株化細胞などの生体電子スピン試料の測定を進める予定です。
ボソニック量子ビット研究の当面の目標は、ボソニック量子誤り訂正コードの一種である、binomial（1,1）コード＊10を超伝導キャビティ中に実装することです。その後、エラー訂正を行い、キャビティの寿命よりも長寿命なボソニック量子ビットの実現、すなわちbreak-even pointの達成をめざします。

＊10 binomial（1,1）コード：ボソニック量子誤り訂正コードの一種。比較的単純なコードで、論理状態はキャビティ中の光子数状態を用いて|0_L〉=（（|0〉+|4）/√2、|1_L〉=|2〉と定義されます。補助量子ビットを用いると、キャビティ中の量子状態を保ったまま、光子数の偶奇性を測定することが可能です。測定された偶奇性が奇数の場合は光子ロスが起きたと見なし、光子を追加することで量子誤り訂正が可能となります。

■参考文献
（1）　角柳・松崎・樋田・山口・齊藤・Munro：“巨視的スケールでの実在性の破れを実証,” NTT技術ジャーナル，Vol.29，No.5，pp.20-23，2017.
（2）　齊藤・角柳・Ashhab・吉原・布施・仙場：“光子と人工原子から成る安定な分子状態を発見,”NTT技術ジャーナル，Vol.29，No.3，pp.67-71，2017.
（3）　H. Toida, Y. Matsuzaki, K. Kakuyanagi, X. Zhu, W. J. Munro, H. Yamaguchi, and S. Saito: “Electron paramagnetic resonance spectroscopy using a single artificial atom,” Commun. Phys., Vol.2, 33, March 2019.
（4）　H. Toida, Y. Matsuzaki, K. Kakuyanagi, X. Zhu, W. J. Munro, K. Nemoto, H. Yamaguchi, and S. Saito:“Electron paramagnetic resonance spectroscopy using a direct current-SQUID magnetometer directly coupled to an electron spin ensemble,” Appl. Phys. Lett., Vol.108, 052601, Feb. 2016.
（5）　R. P. Budoyo, K. Kakuyanagi, H. Toida, Y. Matsuzaki, and S. Saito：“Electron Spin Resonance with up to 20 Spin Sensitivity Measured using a Superconducting Flux Qubit,” Appl. Phys. Lett., Vol. 116, 194001, May 2020.
（6）　K. Kakuyanagi, H. Toida, L. V. Abdurakhimov, and S. Saito: “Submicro­meter-scale temperature sensing using quantum coherence of a superconducting qubit,” New J. Phys., Vol.25, 013036, Feb. 2023.
（7）　F. Arute，K. Arya，R. Babbush，D. Bacon，J. C. Bardin, R. Barends, R. Biswas，S. Boixo，F. G. S. L. Brandao, D. A. Buell, B. Burkett, Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà, J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Yuezhen Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis：“Quantum supremacy using a programmable superconducting processor，”Nature，Vol.574, pp.505-510, Oct. 2019.
（8）　C. Gidney and M. Ekerå: “How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits，” Quantum, Vol.5, p.433, 2021.
（9）　Abdurakhimov・Mahboob・樋田・角柳・齊藤：“ボソニック量子計算に向けた超寿命周波数可変量子ビット,” NTT技術ジャーナル, Vol.33, No.3, pp.23-29, 2021.