インターネットを安全に利用するには情報の暗号化が必要不可欠です。例えば、オンラインショッピングでクレジットカード情報を暗号化せずに送信してしまうと、悪意ある盗聴者に情報を盗まれるかもしれません。現代では、このような場合にRSA暗号などの公開鍵暗号方式が利用されています。これは、現代コンピュータでは計算が難しい問題を利用した暗号（計算量的安全性）ですが、近年さかんに研究されている量子コンピュータが実現すると容易に解読できることが知られています。一方、共通鍵暗号方式の1つに、ワンタイムパッド暗号という手法があります。この暗号は計算が難しいのではなく、解くための情報が足りないという状況を利用した暗号（情報理論的安全性）で、どのようなコンピュータを用いても解読が不可能です。しかし、この解くための情報が足りないという状況をつくるために大きな制約が存在します。通信では情報を0と1のビットとして送信しますが、ワンタイムパッド暗号が安全であるには、本来送信したい情報と同じ長さの乱数＊1（秘密鍵）を送受信者だけが知っている必要があります。直観的にはこの秘密鍵の共有方法があるなら、本来送信したい情報をその手法で送ればよく、限られた状況でしか使えない暗号にみえます。
この課題を解決する技術が量子鍵配送（QKD）です。図1のように、QKDでは量子状態をコピーしようとすると状態が変化することを利用して、情報がどの程度外部に漏洩したかを見積もることができます。通信路で一切漏洩しないわけではないため、暗号化したい情報を直接送ることはできません。しかし、漏れても意味のない乱数を送信すれば、後から漏洩分の情報を消去することで外部漏洩のおそれのない秘密鍵をつくることが可能です。この秘密鍵をワンタイムパッド暗号と組み合わせれば、解読不可能な暗号通信を実現できることになります。
近年報道などでもよく目にするようになったQKDですが、1984年の最初の提案^（1）から約40年もの間研究が続いている技術です。NTTにおいても、理論的な安全性解析や実装実験に加え、独自のプロトコルである差動位相シフトQKDの提案実証など、長年にわたり研究を続けてきました^（2）。今回は、最新の取り組みである高次元QKDと、そのエラー耐性向上技術について紹介します。

＊1　乱数：事前に予測することが不可能なランダムな数値。

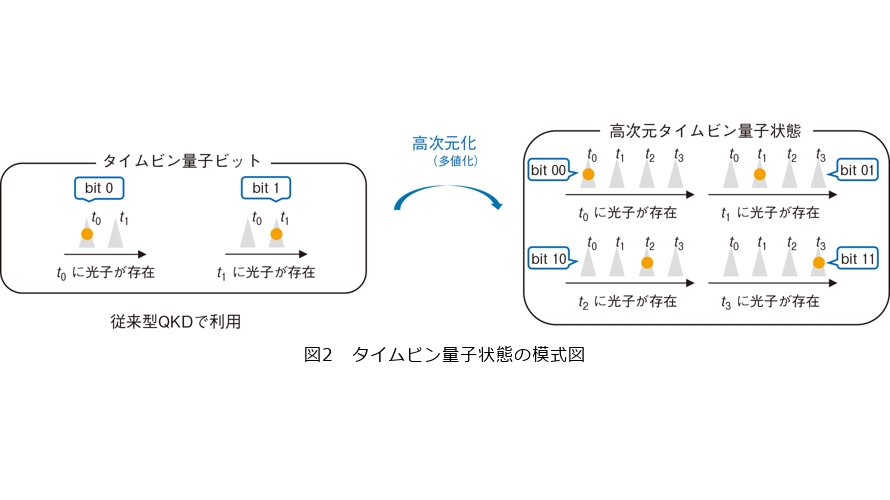
高次元QKDは、高次元量子状態と呼ばれる量子状態を用いることで、QKDの通信速度にあたる秘密鍵生成率を向上させる技術です。従来型のQKDでは、0と1の情報を光の量子状態で表現した量子ビットを利用します。私たちが研究しているタイムビン量子状態の場合、2つの時間位置を考えて、そのどちらに光子＊2が存在するかで情報を表現します（図2左）。一方、ビットではなく0、1、2、…、と多値の情報を表現することで、光子当りの情報量を増加させることが可能です（図2右）。このような多値の情報を扱う状態が高次元量子状態であり、通常の光通信でのPAM＊3やQAM＊4などに類似したコンセプトといえます。実際に、4つの時間位置を利用した4次元タイムビン量子状態を使って、QKDとしては非常に高速な26.2Mbit/sの秘密鍵生成が報告されています^（3）。
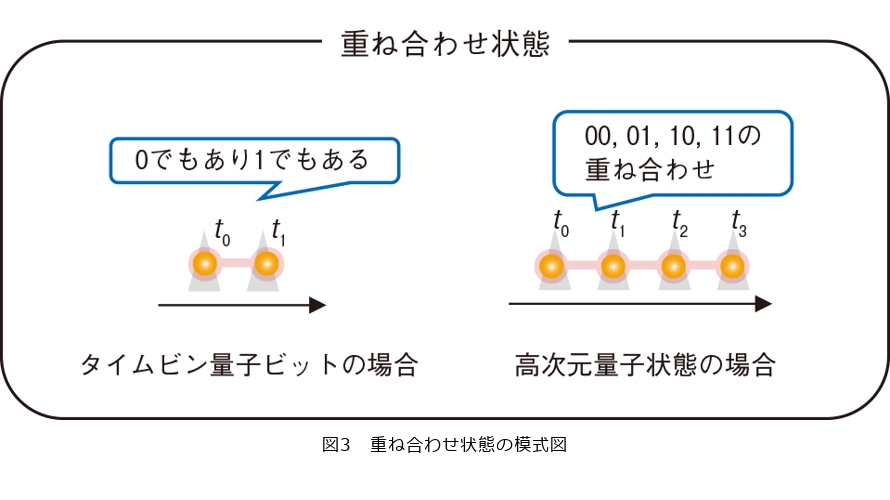
先ほど説明したように、安全な鍵共有を行うには、送信した乱数がどの程度外部に漏れたかを見積もることが重要です。このために、QKDではいわゆる重ね合わせ状態を利用します。量子ビットの場合は0か1かが本質的に分からないような状態、高次元の場合は0、1、2、…のどの値であるかが本質的に分からないような状態です（図3）。中でも特に、相互不偏というある特殊な関係にある重ね合わせ状態を利用することで、送信した乱数がどの程度外部に漏れたかを見積もることができます。d次元の場合、この特殊な関係にある状態の測定は最大で（d+1）種類行うことが可能です。先ほどの26.2Mbit/sの鍵生成実験では、2種類の測定を使って乱数がどの程度外部に漏れたかを見積もっています。一方で、（d+1）種類の測定が実装できれば、通信路での量子状態の変化についてさらに多くの情報を得ることができます。そのため、外部に漏れた情報をより正確に見積もることで、鍵生成率の改善が可能です。つまり、よりエラーに強い高次元QKDが実現できます。
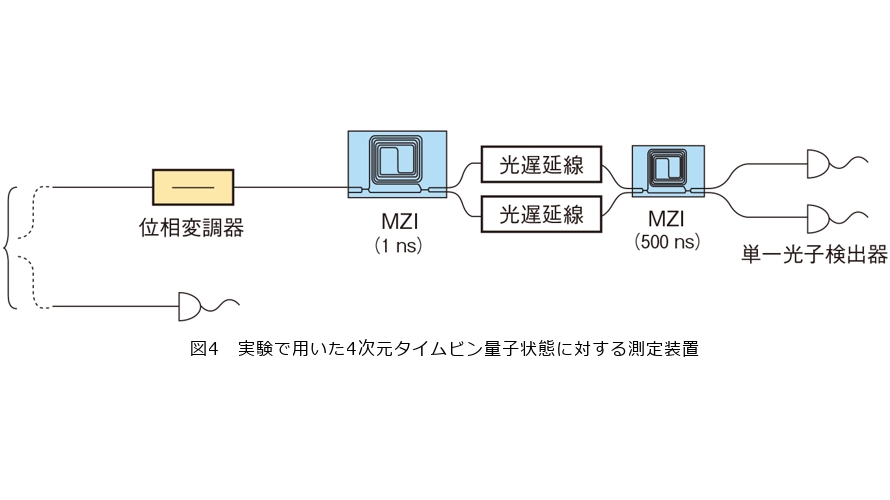
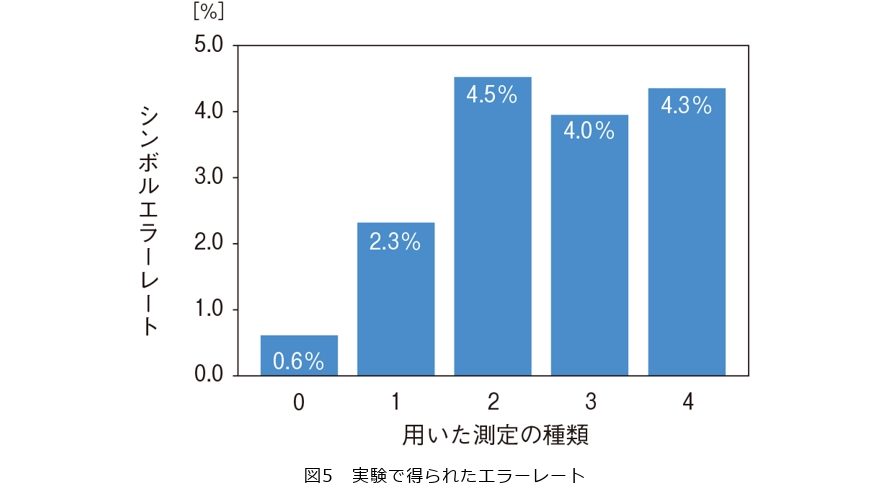
今回NTTでは、この（d+1）種類の測定を、タイムビン量子状態に対してスケーラブルに実装する手法を提案・実証しました^（4）。タイムビン量子状態の測定には、遅延マッハツェンダー干渉計＊5（MZI）や光子検出器を利用します。先行研究では2種類の測定の実装だけでも、（d−1）個のMZIと（d+1）個の光子検出器が必要でした。今回の提案手法を用いると、d＝2^Nの場合ではN個のMZI、さらに、dに関係なく3個の光子検出器と1台の光位相変調器を使うことで、（d+1）種類の測定をすべて実装することができます（図4）。実際に4次元タイムビン量子状態に対する5種類の測定を行い、秘密鍵生成に必要なしきい値よりも十分小さなエラーレートの観測に成功しました（図5）。したがって、今後この測定装置を利用することで、エラーに強い高次元QKDの実装が期待できます。

＊2　光子：光を極限的に弱めたときに観測できる、光のエネルギーの最小単位。素粒子の一種。
＊3　PAM：パルス振幅変調の略称。光や電波の振幅を複数の値に設定して情報を表現し、通信を高速化する手法。
＊4　QAM：直交振幅変調の略称。光や電波の振幅と位相両方を利用して情報を表現し、通信を高速化する手法。
＊5　遅延マッハツェンダー干渉計：光を二分岐した後、一方に時間遅延を与えてから合波する光干渉計。タイムビン量子状態の測定や、光通信の差動位相検波などに用いられます。

先ほど（d+1）種類の測定により、エラーに強い高次元QKDが実現できると説明しました。しかしながらこの手法で厳密に安全性を示すことができるのは、dが素数（2、3、5、…）の場合に限られていました。そのため、今回実装した4次元の場合は当てはまらず、このままでは厳密な安全性を保証できません。そこで今回、既存の安全性証明^（5）の素数の累乗次元（2,4,8や3,9,27など）への拡張にも取り組みました。安全性証明では、量子状態に対する操作を記述する演算子というものを利用します。実は既存の安全性証明で使われていた演算子に対応して、符号理論などで利用されるガロア体＊6を利用して一般化した演算子が存在することが知られています^（6）。ガロア体はdが素数の累乗の場合に用いることが可能なため、この一般化した演算子を使って既存の証明を拡張することで、素数の累乗次元でも厳密な安全性を示すことができました。これにより、先ほどの4次元の測定装置を使った高次元QKDでも、安全性を保証することが可能になります。

＊6　ガロア体：有限個の要素の中で四則演算（＋、−、×、÷）が適切に行えるように計算ルールを定めた集合。有限体とも呼ばれます。

QKDの高性能化に向けたNTTの最近の取り組みとして、高次元QKDとそのエラー耐性向上技術について紹介しました。今回私たちが行ったのは、そのようなQKDのための状態生成装置と測定装置に関する実証実験です。実際にQKDを行うためのシステムとして実装するためには、有限長解析として知られる統計誤差の影響の取り込みなど、まださまざまな課題が残っています。また、原理の説明で紹介した相互不偏という性質はQKD以外の量子通信・量子情報処理でも現れるため、提案装置のQKD以外への応用探索も重要な課題です。今回は高次元状態を使ったアプローチの紹介でしたが、これに限らずNTTでは今後も量子技術の高性能化に向けて精力的に取り組んでいきます。

■参考文献
（1）　C. H. Bennett and G. Brassard:“Quantum Cryptography: Public Key Distribution and Coin Tossing,” in Proceedings of IEEE International Conference on Computers Systems and Signal Processing, pp. 175–179, 1984.
（2）　特集：“量子暗号,”NTT技術ジャーナル, Vol.23, No.6, pp.38–66, 2011.
（3）　N. T. Islam, C. C.W. Lim, C. Cahall, J. Kim, and D. J. Gauthier:“Provably secure and high-rate quantum key distribution with time-bin qudits,”Sci. Adv., Vol.3, No.11, e1701491, 2017.
（4）　T. Ikuta, S. Akibue, Y. Yonezu, T. Honjo, H. Takesue, and K. Inoue:“Scalable implementation of （d+1） mutually unbiased bases for d-dimensional quantum key distribution,”Phys. Rev. Res., Vol.4, No.4, L042007, 2022.
（5）　L. Sheridan and V. Scarani:“Security proof for quantum key distribution using qudit systems,”Phys. Rev. A, Vol.82, No.3, 030301（R）, 2010.
（6）　T. Durt, B.-G. Englert, I. Bengtsson, and K. Życzkowski:“On mutually unbiased bases,”Intl. J. Quantum Inf., Vol.8, No.4, pp.535–640, 2010.