大規模な汎用量子計算機が実用化されると、悪意のある攻撃者がそれを使って暗号技術を破ってしまうかもしれません。そうした攻撃に備えて、今のうちに、これまでの暗号技術がどこまで耐えられるのか、しっかりと検証しておく必要があります。
暗号技術の中でも「SHA-2」は重要なアルゴリズムで、普段PCやスマートフォンを使ってWebサイトを見る際にも使われ、高度情報化社会を裏から支えています。SHA-2は「（暗号学的）ハッシュ関数」の一種に分類される、NIST（米国国立標準技術研究所）標準の暗号技術です。ハッシュ関数は狭義の「暗号」ではないのですが、さまざまな別の暗号技術の一部に用いられたり、そのような暗号技術の安全性に深く関連していたりすることから、広義の「暗号技術」に含まれます＊1。
狭義の暗号の主な役割は、メッセージを暗号化して内容を書くことです。当然ながら、（秘密鍵があれば）暗号文を元のメッセージに戻せる必要があります。それに対してSHA-2のようなハッシュ関数hの役割は、メッセージMを入力してランダムな値h（M）を出力することであり、Mの内容を隠すことではありません。別々のメッセージMとM’のペアであってh（M）＝h（M’）を充たすようなものを「衝突」というのですが、安全なハッシュ関数とは、衝突を発見しようという攻撃に耐える（＝衝突耐性を持つ）ことが要請されます（表1）。
ここで与えられているのは、ハッシュ関数h＊2のみです。攻撃者はとにかく何でも構わないので、h（M）＝h（M’）を充たすMとM’を見つければ「勝ち」です。その意味で衝突攻撃は「暗号文を解読する」のとは少し異なります。「暗号文を解読する」とは、（狭義の暗号で）暗号化された暗号文が与えられて、元のメッセージを復元しようとする攻撃だからです。
なお、「衝突攻撃にどれだけ耐えるか」といっても限界があります。この限界を説明する重要な概念が「誕生日のパラドックス＊3」です。この概念を応用すると、nビット出力のハッシュ関数の衝突を計算量2^n/2で発見できる、ということが分かります。誕生日攻撃は、ハッシュ関数がどれだけ安全でも適用できる汎用的な攻撃なのです。
ひるがえって、（古典計算機を用いた攻撃に対して）安全なハッシュ関数は、計算量2^n/2を掛けないと衝突が発見できないことが要請されます。例えば、とあるハッシュ関数の衝突を2^n/2未満の計算量で発見する専用攻撃の存在が分かった場合、その関数には特有の弱みがあって破られた、とみなされます。いわば、誕生日攻撃の計算量2^n/2は、特定のハッシュ関数を対象にした専用の攻撃が意味のある攻撃かどうかの判定基準になっているのです。

＊1　実用的なハッシュ関数の設計は、主に（狭義の）共通鍵暗号の設計技術を流用することが多いことから、共通鍵暗号技術に含められます。
＊2　より正確には、hを計算するアルゴリズム。
＊3　誕生日のパラドックス：ある人の誕生日は365通りあるはずだが、20人程度ランダムに人を集めて誕生日を聞くと、かなり高い確率で同じ日が誕生日のペアが見つかるというもの。

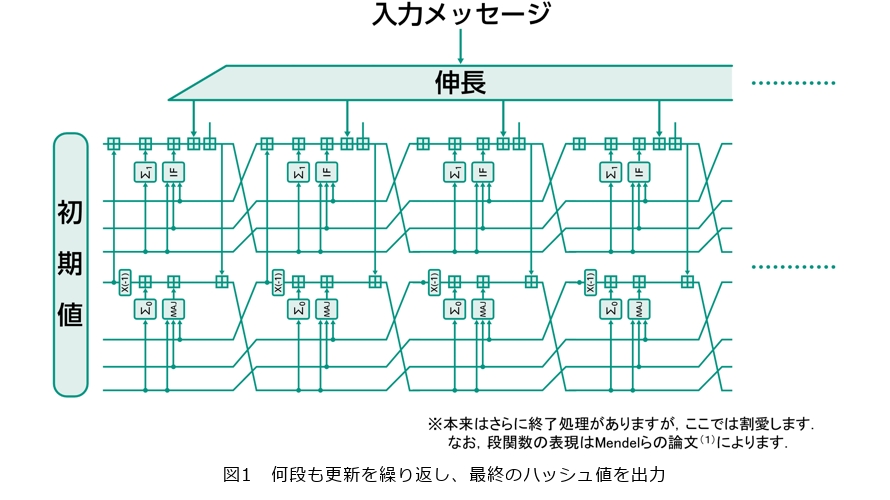
具体的には、SHA-2が出力を計算する仕組みは、次のとおりです。まず、入力されたデータが、大量の「メッセージブロック」の列に伸長されます。各メッセージブロックは、内部状態の値を更新させるのに使用されます。初期状態からスタートしてメッセージブロックを用いて内部状態を繰り返し何度も変化させることにより、最終の出力（ハッシュ値）が計算されます（図1）。
このように、SHA-2をはじめ、典型的なハッシュ関数の設計は、似たような処理を何段も繰り返し、一般にこの処理回数を減らせば減らすほど、安全性は弱まります。そのため、手掛かりが何もないような状況から何の予兆もなく天才的な攻撃方法が突然発見されるようなことは、滅多に起こりません。したがって、安全性を測る指標は「どこまで弱めれば破れてしまうか」という考えになります。
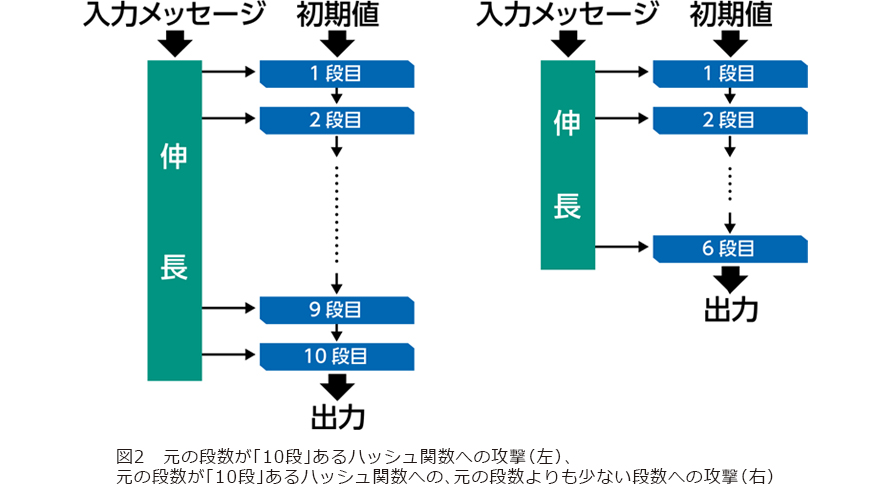
例えば、元のハッシュ関数が10回の処理を繰り返す構造をしていたとして（図2左）、「この処理回数を6段まで減らせば2^n/2より小さい計算量で衝突が見つかってしまう」ということが分かるのであれば、その関数は6段まで破れてしまう、という言い方をします（図2右）。
また、本来の元の段数まで破られたとき、そのハッシュ関数は破れたことになりますが、元の段数に達していなくても、破られる段数が伸びれば「意味のある攻撃」とみなすことができます。
このように、その道のプロが注意深く設計したハッシュ関数が破れる際は、多くの場合、破れる段数が徐々に伸びていって、最終的に元の段数が破れる、という経過を多くの場合たどります。「世界中の研究者がよってたかって攻撃を試みたが、かなり弱めないと攻撃が成功しない」という事実が、ハッシュ関数の安全性を担保しているのです。

SHA-2のようなハッシュ関数は素因数分解のような綺麗な代数的構造を持たないため、量子計算機ができたからといってすぐに破れるようになることはないだろうと考えられてきました。唯一、汎用衝突攻撃＊4の計算量が誕生日攻撃の2^n/2から2^n/3にまで落ちることは判明していました（＝BHTのアルゴリズム）。ただし、下げ幅がそれほど大きくないこともあり、「特段問題ないだろう、あるいはnが少し大きいハッシュ関数を使えば良いだろう」と受け止められてきました。
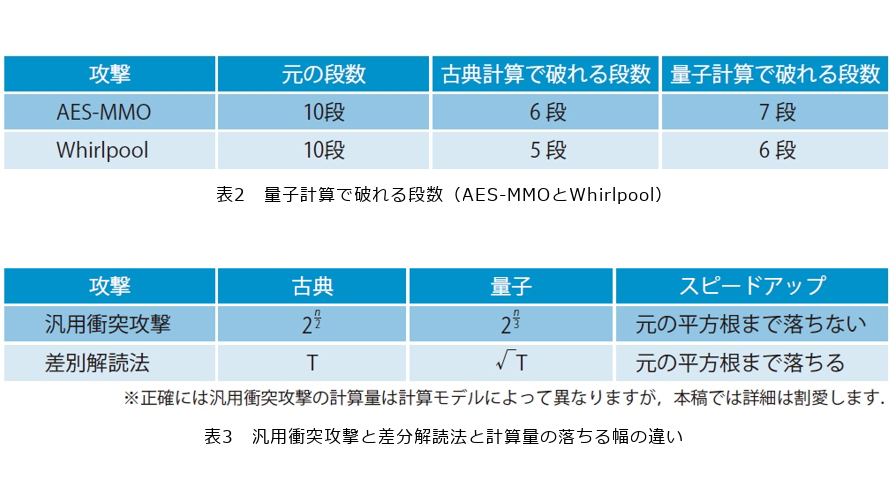
ところが研究を進めてみると、事態はそう単純ではありませんでした。まず、「AES-MMO」や「Whirlpool」といったハッシュ関数については、量子計算機によって1段多く破られることが分かりました（表2）。これまで堅牢であった暗号に対して、量子計算機は明らかに古典計算機よりも破る力があるのです^（2）。
攻撃可能段数の伸びについては、「汎用衝突攻撃の計算量がさほど落ちない一方、特定のハッシュ関数をターゲットとした専用攻撃の計算量が落ちる幅はより大きくなることがあるため、専用攻撃の威力は相対的に高まる可能性がある」という考え方が根底にあります。例えば「グローバーのアルゴリズム」という量子アルゴリズムを使うと、専用攻撃によく使われる「差分解読法」の計算量は元の平方根程度まで落ちる可能性があることがすでに分かっていました^（3）。一方、汎用衝突攻撃の計算量はBHTのアルゴリズムより下がらないことが証明されており、計算量が落ちる幅は元の平方根までには至りません（表3）。
これまでみてきたように、ハッシュ関数の（古典的な）安全性評価指標の1つは、段数をどこまで削れば破れるかということでした。そして特定の段数まで段数を削ったハッシュ関数への専用攻撃が有効かどうかは、その攻撃の計算量が汎用攻撃の計算量を下回っているかどうかで判定されていました。量子計算機が利用可能な世界では、攻撃成立の判定基準となるべき汎用攻撃の計算量がさほど変わらない一方、専用攻撃の計算量が相対的に下がるため、古典の世界よりも有効だと判定される専用攻撃の種類が増えると結論付けざるを得ないわけです。
量子計算機が利用可能な想定下で、そうした「基準」をどうとらえるべきかに着目した研究がない中で、7段AES-MMOや6段Whirlpoolへの衝突攻撃が、古典的には有効と判定されないにもかかわらず、量子計算機を利用可能な世界では有効と判定され、前述の着眼点の重要性を実証する具体例となりました。

＊4　汎用衝突攻撃：誕生日攻撃のように、どれだけ安全なハッシュ関数にも適用できる衝突攻撃。

ただし、AES-MMOやWhirlpoolといったハッシュ関数は、SHA-2と比べるとマイナーで、利用シーンもかなり限られています。そこで、現在もっとも広く使われているハッシュ関数であるSHA-2でも攻撃可能段数が伸びるのか、という疑問が自然と出てきます。これが今回の最大のテーマです。
そして実際に検討を重ねたところ、やはり段数が伸びるという結果が得られたのです。「SHA-2」は実は総称で、出力長が違ういくつかの関数が含まれているのですが、このうちのSHA-256やSHA-512について、古典的には有効でないが量子計算機のある世界では有効と判定される攻撃を見つけました^（4）。
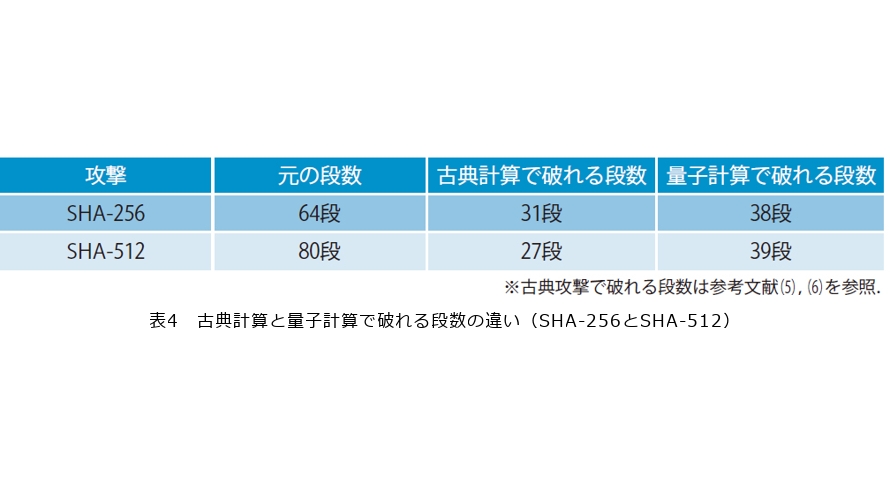
SHA-256は64段の処理を行っていますが、古典計算機を用いた場合、衝突耐性としては31段まで減らして弱めれば破られることが知られています。つまり、32回以上の処理が行われた際に衝突耐性を破るような攻撃は見つかっていませんでした。ところが、量子計算機が利用可能な世界では、38回程度でも衝突耐性が破れてしまうことが分かったのです。つまり、量子計算機はSHA-2の安全性に影響を及ぼすといえるわけです。SHA-512についての結果も、基本的には同様です（表4）。
もちろん、この結果から直ちにSHA-2の衝突耐性が破られた、ということにはなりません。まだまだSHA-2は安全に使えます。しかしこの結果は、量子計算機はSHA-2の安全性にさほど影響を及ぼさないのではないかという従来の大雑把な見方は改めるべきだ、ということをはっきりと示しています。

ほんのわずかな期間で情報通信技術は急速な進化を遂げ、それに伴い、セキュリティの要となる暗号技術もしっかりと整備されてきました。その結果、誰もが利用できる世界中で共通の国際標準の暗号技術が打ち立てられています＊5。これまでも何度となく、それまで用いられていた暗号技術の脆弱性が指摘され、早い段階でより強固な暗号を開発してきた歴史がありますが、量子計算機を想定した攻撃の研究については、まだまだ研究すべきことがたくさんあります。
社会で極めて重要な役割を果たしているSHA-2の安全性についてさえ、これまでよく分かっていなかったのですが、量子計算機が利用可能な世界では破れる段数が伸びると結論付けざるを得ないことが今回示されました。
今後も、未知の攻撃がないか探究を続けていく必要があります。こうした攻撃の研究で得た知見がフィードバックされれば、今後、より安全なハッシュ関数が設計されることになるでしょう。また、こうした攻撃の研究を公にすること自体が、もっと世の中の安全性を高めてゆくことにつながっていると思います。攻撃側もすでにこっそりと同じような研究をしているかもしれませんので、さらにその先を見越して、量子計算機による攻撃を想定し、それに十分耐えられる暗号をつくることがめざされます。どうしても日常生活の感覚とは異なる次元の問題ですから、なかなか実感がつかみにくいかもしれませんが、量子計算機が実用化される中では、こうした問題を攻撃者に先立って検討することが要請されます。
各暗号技術をターゲットとする専用の攻撃自体は、その暗号技術の内部構造をフルに利用しているため、他の研究への応用はあまり考えられません。しかし暗号技術の安全性は私たちの日常の暮らしと密接に関連していることから、広範に興味を持ってもらえるのではないかと期待しています。

＊5　近年の量子計算機の急速な発展状況を受けて、NISTは耐量子暗号技術、特に公開鍵暗号（およびKEM）や電子署名の標準化作業に取り組んでおり、世界中から幅広い方式が集まっています。2023年1月の時点で選考はすでに一部が終わり、標準化されることが決定したものもあります。

■参考文献
（1）　F. Mendel, T. Nad, and M. Schläffer:“Finding SHA-2 Characteristics: Searching through a Minefield of Contradictions，”ASIACRYPT 2011,Proc. of LNCS, Vol. 7073, pp. 288-307，2011.
（2）　A. Hosoyamada and Y. Sasaki:“Finding Hash Collisions with Quantum Computers by Using Differential Trails with Smaller Probability than Birthday Bound，”EUROCRYPT 2020, Proc. of, Part II. LNCS, Vol. 12106, pp. 249-279，May　2020.
（3）　M. Kaplan, G. Leurent, A. Leverrier, and　M. N. Plasencia:“Quantum differential and linear cryptanalysis，” IACR Trans. Symmetric Cryptol. 2016（1）, pp. 71–94，2016.
（4）　A. Hosoyamada and Y. Sasaki:“Quantum Collision Attacks on Reduced SHA-256 and SHA-512，”CRYPTO 2021, Proc. of, Part I. LNCS, Vol. 12825, pp. 616–646， 2021.
（5）　F. Mendel, T. Nad, and M. Schläffer:“Improving Local Collisions: New Attacks on Reduced SHA-256，”EUROCRYPT 2013, Proc.of LNCS, Vol. 7881, pp. 262-278，2013.
（6）　C. Dobraunig, M. Eichlseder, and F. Mendel:“Analysis of SHA-512/224 and SHA-512/256，”ASIACRYPT 2015, Proc.of Part II. LNCS , Vol. 9453, pp.612-630，2015.