多くの物理現象のダイナミクスは、ニュートンの運動方程式のような「微分方程式」を用いて記述されます。これまでの歴史では、各分野の専門家たちが現象の観察や理論的検討を通じて、現象を再現するために適切な方程式を導き出してきました（図1上）。これらの方程式を解くことで物理現象のシミュレーションが可能となり、実際に物理実験をすることなく、計算機上で、さまざまな条件における現象を再現することができます。物理シミュレーションは、気象予測や航空機設計など、実世界におけるさまざまな場面で活用されています。しかし、方程式の設計には多大なコストがかかることや、実世界における気象現象など、複雑な現象のモデル化には限界があるという問題がありました。
一方、昨今の情報通信技術の進展により、データ駆動型アプローチが注目を集めています。特に、機械学習技術の発展により、実世界におけるさまざまな問題が、大規模なデータを活用することによって非常に高い精度で解けることが明らかになっています。では、機械学習技術を用いて物理現象のシミュレーションをすることも可能でしょうか。このような課題に対して、私たちは、観測データから物理現象を正確に再現するための機械学習技術について研究を進めています。上述した従来のアプローチと異なり、現象に合わせて方程式を設計することなく、データから高精度なシミュレータを自動構築できる技術の研究に取り組んでいます（図1下）。

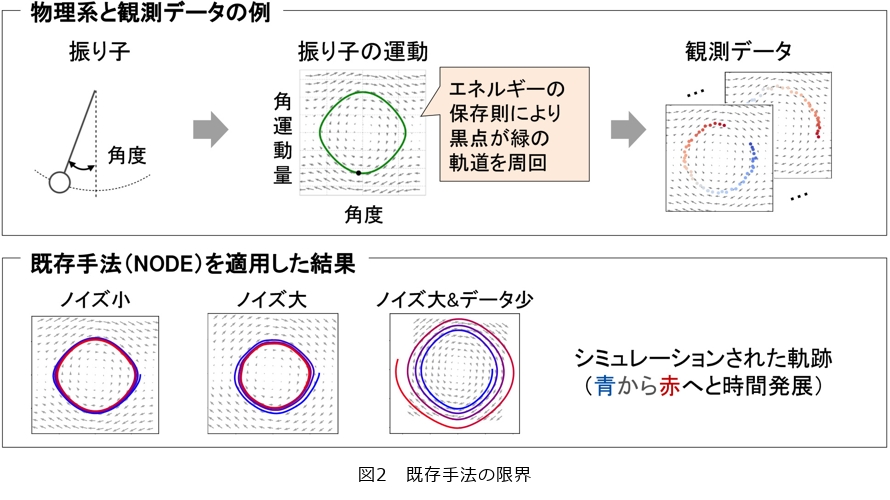
前述のような研究の流行の背景には、ある技術的なブレークスルーがありました。2018年に発表されたニューラル常微分方程式（NODE：Neural Ordinary Differential Equation）^（1）です。NODEでは、方程式をニューラルネットワークにより代替（図1内オレンジ色の枠「機械学習モデル」を参照）し、観測データを用いてニューラルネットワークのパラメータを学習することにより、方程式を設計することなく現象を表現します。では、物理現象を観測したデータにNODEを適用すれば、十分な精度のシミュレーションができるでしょうか。実は、それだけでは高精度なシミュレーションは難しいことが分かっています。図2では、単純な物理系として振り子を例とした実験結果を紹介します。振り子は、角度を横軸、角運動量を縦軸にとると、図2の真ん中上に示すような運動として描くことができます。エネルギー保存則が成り立つため、黒い点が緑の軌道上を周回し続けます。このような運動を観測したデータ（図2右上）が与えられたとしたとき、NODEを用いてシミュレーションを行った結果を図2下に示しています。シミュレーションされた軌跡が、緑で表す正解の軌道から離れていってしまう様子が分かります。特に、観測データに含まれるノイズが大きく、かつ、データが少ない状況においては、シミュレーションの精度が著しく低下してしまうことが分かります。

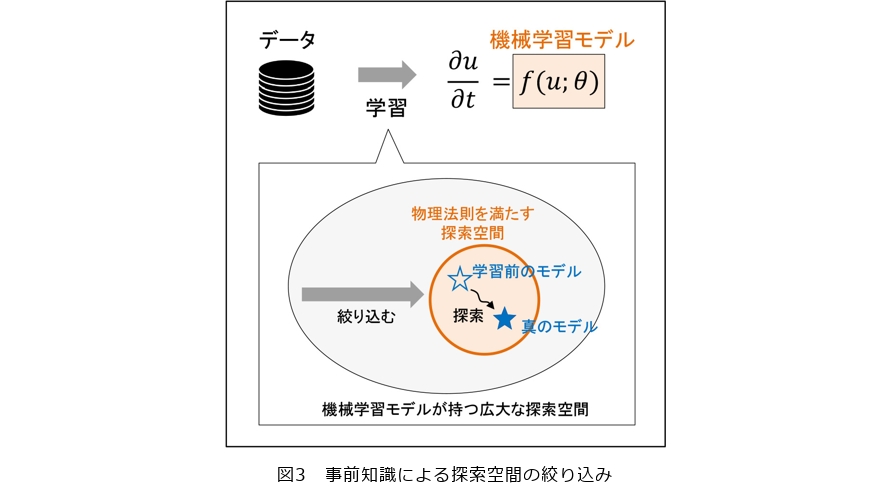
では、なぜこのような結果となってしまうのでしょうか。機械学習モデルは非常に高い表現力を持つことが知られ、大規模かつ複雑な物理現象を適切にモデル化できる可能性を秘めています。しかし、高い表現力を持つがゆえに、「機械学習モデルが持つ広大な探索空間」（図3の灰色の領域）から物理現象を正確に再現するモデルを推定するのは簡単なことではありません。特に、少量のデータしか与えられない場合や、データにノイズや欠損が多く含まれるような場合には、学習はより一層難しくなります。

データが少なく、かつ、データにノイズや欠損が多く含まれる場合には、適切な学習を導くためのヒントとなるような「事前知識」の導入が有効です。物理学に由来する事前知識を学習に活用することを目的とした研究分野は、Physics-Informed Machine Learning^（2）と呼ばれており、近年研究が活発になり始めています。これにより、探索空間を絞り込み、物理現象を正確に再現するモデルを効果的に推定できることが期待されます（図3のオレンジ色の領域）。事前知識を導入するためのもっとも素朴な方法は、図1の従来のアプローチに記載したような方程式を仮定し、方程式に含まれる物理パラメータ（図1のαやβ）をデータから学習することが考えられます。しかし、この方法では、探索空間を絞り込みすぎてしまい、機械学習モデルの持つ高い表現力を活かせず、既知の方程式では表しきれないような複雑な現象には適用することが困難です。そこで、私たちは、物理現象であれば満たすべき「物理法則」を事前知識として組み込むという方法に着目しました。これにより、機械学習モデルの表現力を維持しつつ、探索空間を適切に絞り込んだうえで学習を行うことができます。

これまでの歴史において、エネルギー保存則や質量保存則、運動量保存則などさまざまな物理法則が発見されてきました。本稿では、力学系において広く成立するエネルギー保存則を機械学習モデルに組み込んだ研究事例について紹介します。エネルギー保存則に従う物理現象を表現するには、「ハミルトン力学」の理論を用いるのが便利です。ハミルトン力学では、物理現象を表す方程式を設計するのではなく、物理系が持つエネルギー関数を設計します。エネルギー関数を決めることができれば、「ハミルトンの運動方程式」に従って、物理ダイナミクスは機械的に導出することができます。ここで重要なことは、ハミルトンの運動方程式に従って導出されたダイナミクスは、常にエネルギー保存則に従うことを保証できる、ということです。従来手法のハミルトニアンニューラルネットワーク（HNN：Hamiltonian Neural Network^（3））は、物理現象ごとに設計が必要であったエネルギー関数をニューラルネットワークに置き換えることで、エネルギー保存則に従う物理現象をデータから推定する方法を提案しました。しかし、ニューラルネットワークに基づく手法は、十分な質と量のデータが使えることを暗に仮定しており、そのようなデータが得られない状況においては過学習＊1を起こし、精度が低下してしまうという問題がありました。
そこで、私たちは、ノイズを含み、かつ、少ないデータからの学習に有利な機械学習モデルである、ガウス過程＊2を基礎として、ハミルトン力学の理論を組み込んだ新たな手法を提案しました^（4）〜^（6）。提案手法の模式図を図4に示します。提案手法は3つの特徴を持ちます。1番目は、エネルギー関数をニューラルネットワークではなく、ガウス過程により推定します。これにより、学習に用いるデータが少ない状況においても過学習を避けてエネルギー関数を推定することが期待できます。2番目は、ハミルトンの運動方程式によりダイナミクスを導出します。ガウス過程に従うダイナミクスが、常にエネルギー保存則を満たすことを保証することができます。3番目は、データにノイズを含むことを仮定した観測モデルを導入します。これにより、ノイズが大きいデータからでも頑健な学習が期待できます。提案手法を用いることにより、十分な質と量のデータが得られない場合でも、エネルギー保存則に従う物理現象を効果的に学習可能とし、高精度なシミュレーションを行うことができます。
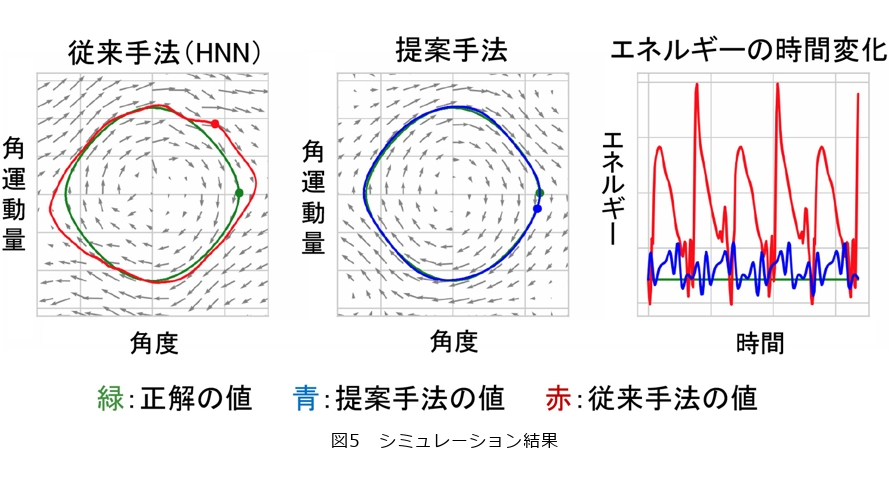
図5は従来手法（HNN）と提案手法を用いて、振り子の運動をシミュレーションした結果です。図5の左と中央を比較すると、緑で表される正解の軌跡に対して、提案手法は、より正確にシミュレーションができていることが分かります。図5の右は、エネルギーの時間変化をプロットしたものです。緑で表される正解の値は、エネルギー保存則により、一定の値を取ります。赤で表される従来手法の推定値に比べ、青で表される提案手法の推定値は、より正確にエネルギーの値をとらえられていることが分かります。このような結果から、提案手法はエネルギー保存則をうまくとらえつつ高精度なシミュレーションに成功していることが分かります。

＊1 過学習：機械学習モデルが、与えられたデータに対して過剰に適合してしまうこと。これにより、未知のデータが与えられた際の予測精度が低下してしまいます。
＊2 ガウス過程：任意の連続関数を近似可能な確率モデル。予測に対する不確実性を扱うことができ、データに含まれるノイズや欠損の悪影響を低減してモデルを学習することが可能。

現時点では、学習に必要な入力データや、表現可能な物理現象の種類に、まだまだ制限があります。今後は、実世界への適用を想定し、より現実的な観測から、より複雑な現象の再現をめざしていきます。今回紹介した研究では、振り子の角度のような物理変数が観測できることを仮定しました。しかし、物理系が複雑になると、そのような変数を直接観測することは難しい状況が容易に想定されます。一方で、物理現象に関連するセンサの値や、画像や動画であれば、比較的観測がしやすいことが考えられます。そのようなさまざまな形式の入力が与えられたときでも、物理現象を再現できるような技術が必要だと考えています。また、気象現象など、実世界の複雑な現象は、「偏微分方程式」と呼ばれる種類の方程式で表されることが多く、そのような方程式への技術の拡張が望まれます。
本研究分野が発展すれば、さまざまな応用が期待できます。例えば、気象予測を行うことにより、気候変動のような環境問題への対処や、台風や津波のような現象を再現し、防災に役立てることもできます。具体的な方程式で表しきれない複雑な気象現象をより正確にシミュレーションすることで、高精度な予測結果を得ることが期待できます。また、航空機や自動車、半導体デバイスなどは、現在も物理シミュレーションを活用して製品設計が行われています。観測データから物理シミュレータを自動的に獲得することができれば、新しい製品をつくる際のシミュレータの高精度化や効率化を行うことができます。さらに、ロボットによるシーン理解や推論といった、AI（人工知能）分野への展開も考えられます。例えば、人間は乱雑に積まれた荷物の画像を見ると、もしかしたら崩れるかも、といった推論を行いますが、このように推論できるのは、人間が過去の経験に基づいて、無意識のうちに、物理現象を学んでいるから、とも考えられます。今回の研究のアイデアを用いて、ロボットが物理現象を学習するようになれば、上記のような状況におけるリスク回避を行うことも可能ではないかと考えています。

本研究は、JST、ACT-X、JPMJAX210Dの支援を受けたものです。

（1）　R. T. Q. Chen, Y. Rubanova, J. Bettencourt, and D. K. Duvenaud：“Neural ordinary differential equations,” NeurIPS 2018, Vol. 31, Dec．2018.
（2）　G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, and L. Yang：“Physics-informed machine learning,” Nature Reviews Physics, Vol. 3, No. 6, pp. 422-440, 2021.
（3）　S. Greydanus, M. Dzamba,and J. Yosinski：“Hamiltonian neural networks,”NeurIPS, Vol. 32, 2019.
（4）　Y. Tanaka, T. Iwata, and N. Ueda：“Symplectic spectrum Gaussian processes: Learning Hamiltonians from noisy and sparse data,” NeurIPS 2022, Nov．2022.
（5）　田中・岩田・上田：“エネルギーの保存・散逸則を満たすガウス過程モデル，”第25回情報論的学習理論ワークショップ，2022．
（6）　田中：“ガウス過程と物理現象のモデル化（特集「AIとシミュレーション」），”人工知能学会誌，Vol. 38，No. 3，pp.318-325，2023．