1994年に、当時ベル研究所に所属していたピーター・ショア氏が量子コンピュータで素因数分解を高速に行うためのアルゴリズムを発見しました。素因数分解の困難性は現代暗号の安全性の根拠になっており、現在のコンピュータ（古典コンピュータ）では解くのが困難だと考えられています。ショアのアルゴリズムは量子コンピュータの計算能力の高さを表す有名な例であり、この発見以降、量子コンピュータは世界中で研究されてきました。現在では、物性・化学シミュレーションや、数学の問題であるジョーンズ多項式の近似など、さまざまな問題において、量子コンピュータは古典コンピュータ（の既知の最良のアルゴリズム）よりも高速な計算が可能だということが分かっています。しかし、このような長所がある一方で、量子コンピュータにはノイズの影響によってエラーが発生しやすいという実装上の課題もあります。
量子コンピュータの情報の基本単位である量子ビットを実現する方法にはさまざまなものがありますが、例えば超伝導回路を用いる場合、共鳴周波数の時間的な揺らぎなどによりエラーが発生してしまいます。素因数分解を行う場合、このようなエラーが発生したとしてもあまり問題にはなりません。なぜならば、素因数分解は答えの正否を古典コンピュータで掛け算を行うことでチェックできるため、量子コンピュータの計算途中にエラーが発生して間違った答えを出力してしまっているかどうかが簡単に分かるからです。しかし、上記のとおり、量子コンピュータは素因数分解以外の問題にも応用することが可能です。例えば、ジョーンズ多項式の近似を行うために量子コンピュータを使った場合、出力された数字が正しい近似になっているのか、それとも間違った答えになっているのかを古典コンピュータで高速にチェックする方法は知られていません。言い換えれば、量子コンピュータの高速計算を可能にしている量子重ね合わせによって答えの正否チェックが困難になるというジレンマがあるのです。量子コンピュータの高い計算能力を活用するためには、エラーの影響に対処し、このジレンマを解消するための技術が必要になります。

量子コンピュータの計算途中に発生するエラーの影響を緩和する技術として、本章では「量子エラー訂正・抑制」と「量子計算の検証」について説明します。量子エラー訂正は名前のとおり、発生したエラーを検知し訂正する技術です。そのために、複数の量子ビットで1量子ビット分の情報を保存するということを行います。現在の技術では量子ビットを（高精度に）大量に準備することは困難であるため、量子エラー訂正の実現は小規模での実験にとどまっています。この欠点を解決するのが量子エラー抑制であり、量子ビットの数を増やす代わりに、計算の繰り返し回数を増やすことでエラーの影響を抑制することができます。しかし、期待値の計算など限られた用途にしか使用できない、一般には指数回繰り返す必要があるなどの欠点もあります。また、量子エラー訂正・抑制を適用するためには、どのようなエラーが発生しているかある程度知っている必要があります。特に、量子エラー訂正や一部の量子エラー抑制手法はエラーの発生確率が十分小さくなければ使用することができません。
一方で、量子計算の検証はエラーが大きい場合でも使用することができます。その代わり、エラーを訂正したり抑制したりすることはできず、エラーが発生しているかどうかを検知することしかできません。しかし、量子コンピュータに複数回同じ問題を解かせて各々の答えを検証することで、その中からエラーの影響を受けていない正しい答えを抽出することができるため、検証技術も立派なエラー対策技術だということができます。
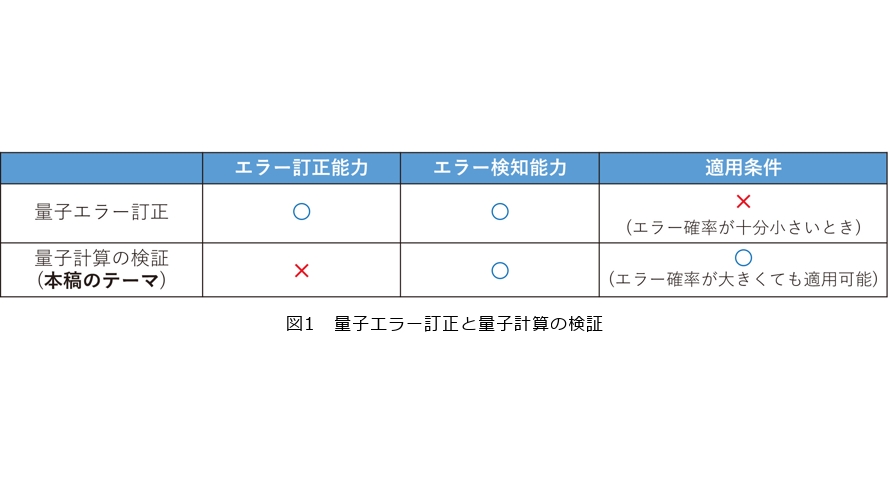
この章の話をまとめると、量子エラー訂正はエラーを訂正できますが、エラー確率が小さいときにしか使えません。一方で、量子計算の検証はエラー確率が大きくても使えますが、エラーを検知することしかできません。このように、これら2つの技術はお互いの欠点を補い合う相補的な関係にあり、信頼性が高い大規模な量子コンピュータの実現をめざすうえで、どちらも大切な技術だといえます（図1）。以降では、量子計算の検証に関する私たちの研究をいくつか紹介します。

量子コンピュータを実現するための方法は数多く提案されており、測定型量子計算はその一種です。通常の方法（量子回路方式）では、最初に初期化した量子ビットを準備し、それらを量子ゲートで操作した後測定することで計算を行います。測定型量子計算では、最初にグラフ状態と呼ばれるエンタングル状態＊さえ準備してしまえば、後はそれを1量子ビットずつ測定するだけで任意の量子計算を行うことができます。さらに、グラフ状態は解きたい問題に依存しないため、計算を開始する前にあらかじめ準備しておくことが可能です。光（厳密には、光子）を用いて量子ビットを実現し、量子ゲートを線形光学素子で実現する場合、1量子ビットに対する操作や測定は比較的簡単に行うことができますが、2量子ビットに対する量子ゲートは実現が難しく確率的にしか行うことができません。測定型量子計算では、2量子ビット操作を行うのはグラフ状態を準備するときだけでよいため、難しい操作は計算開始前に行い、計算開始後は測定という簡単な操作のみでよいという利点があります。このような量子回路方式との違いから、量子暗号や量子通信など、さまざまな量子情報処理に応用されています。
測定型量子計算を用いて量子コンピュータを実現する場合、エラーが一番発生しやすいのがグラフ状態を準備するステップです。そのため、グラフ状態が正しくつくられているかを検証する手法がこれまで数多く提案されてきました。私たちは2019年に、当時の従来手法よりも効率的な検証手法を提案することに成功しました^（1）。このような効率化を行うため、量子暗号の一種である量子鍵配送に使用されていた数学的テクニックを、世界で初めて検証技術に応用しました。その後、私たちの検証技術を量子計測に応用し^（2）、それが中国科学技術大学のグループに小規模ながらも光学実験で実現される^（3）など、本研究は大きな広がりをみせています。

＊　エンタングル状態：量子的な相関がある状態。2個以上の量子ビットを用いて生成することができ、さまざまな量子情報処理に応用されています。

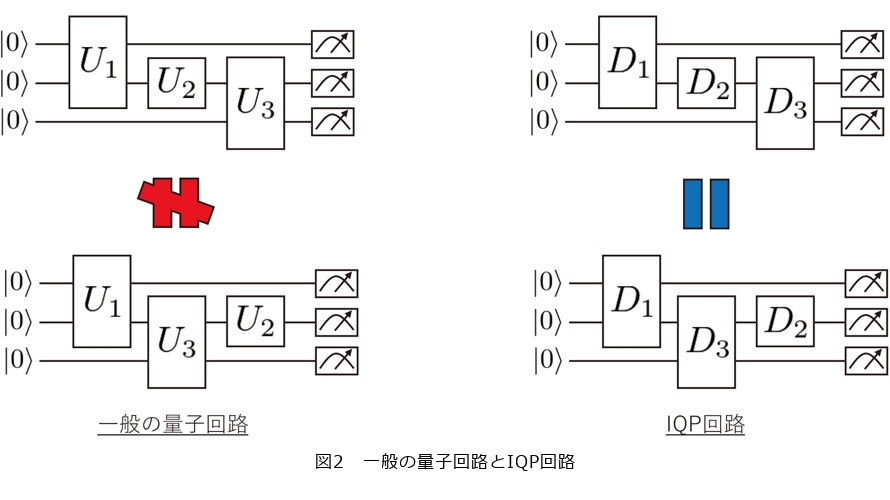
前述したグラフ状態の検証を、重み付きグラフ状態と呼ばれるより複雑な量子状態に拡張することにも成功しています。このような拡張を行うことにより、IQP（Instantaneous Quantum Polynomial time）回路と呼ばれる特別な量子回路が正しく動作しているかの検証が可能となります。通常の量子回路では、量子ゲート操作の順番を入れ替えると異なる計算になってしまいますが、IQP回路では量子ゲート操作を入れ替えても同じ計算になるような限られた計算しか行うことができません（図2）。そのため、計算能力は理想的なフルスペックの量子コンピュータよりも弱いですが、実現はその分簡単だと考えられています。IQP回路を用いることによって、古典コンピュータではつくることが困難な乱数をつくることができます。しかし、これは理想的なIQP回路が実現できた場合の話であり、実際には正しい乱数をつくれているのか、エラーによって古典コンピュータでも簡単につくれる乱数になってしまっているのかを判定することは容易ではありません。2019年、私たちはIQP回路の検証を行うことで、そのような乱数の生成が正しくできているかを高速にチェックすることを可能にしました^（4）。

IQP回路のようにフルスペックの量子コンピュータよりも計算能力が弱い量子コンピュータは、非万能量子コンピュータと呼ばれています。その中でも、特に現在および近未来に実現すると考えられている量子コンピュータは、NISQコンピュータと呼ばれています。NISQとはNoisy Intermediate-Scale Quantumの頭文字で「ニスク」と読み、ノイズがある小・中規模の量子コンピュータを意味しています。本誌 2023年4月号記事『量子コンピュータの能力を引き出すアルゴリズムとその検証技術』^（5）に掲載されているとおり、私たちは2022年にNISQコンピュータ用の検証手法を提案することに成功しました^（6）。

これまで紹介してきた検証手法には、検証するために小規模な量子測定器（読み出し機能のみの量子コンピュータ）が必要だという短所があります。つまり、測定型量子コンピュータ、IQP回路、NISQコンピュータなどさまざまな量子コンピュータの出力が正しいかを、それよりも小規模な別の量子コンピュータで検証する手法になっています。量子計算の検証をより実用的な技術にするためには、量子コンピュータを古典コンピュータのみで高速に検証できることが好ましいといえます。2018年にカリフォルニア大学バークレー校（当時）のウルミラ・マハデフ氏が、そのような古典検証の手法を、耐量子計算機暗号という量子コンピュータでも破ることができない暗号を用いて提案しました。同氏の研究成果は分野の大きなブレークスルーであり、その後多くの研究者によって拡張されました。私たちも、2022年に、同氏の手法を応用することで、マジック状態という特殊な量子状態を正しく準備・測定できているかを検証する手法を提案しました^（7）。マジック状態を用いない量子計算（専門的には、クリフォードユニタリ操作のみの量子計算）は古典コンピュータでシミュレート可能であるため、マジック状態は量子コンピュータを量子コンピュータたらしめている、量子性の証拠といえます。そのため、マジック状態の検証は、量子コンピュータに欠かせない量子性の有無をチェックするために使用することができます。

前述のとおり、私たちはこれまでさまざまな検証手法を提案してきました。これらにより、さまざまな量子コンピュータの検証が可能になりましたが、実用化のためにはさらなる改善が必要です。今後は改善を行うとともに、量子計算の検証をクラウド量子計算システムに応用することもめざしています。現在、IBMやAmazonなどがクラウド量子計算システムを提供していますが、これらには、ユーザが受け取った答えの正否をチェックするための検証機能がありません。既存システムに検証機能を組み込むことで、ユーザ自身で答えの正否をチェックできるようになるだけではなく、システムを提供している企業側も量子コンピュータの性能が高いことを公平なかたちで公表することが可能となります。世界中の誰もが、どこでも量子コンピュータの恩恵を安心して受けられる社会の実現をめざして、今後も量子計算の基礎技術構築に取り組んでいきます。

（1）　Y. Takeuchi, A. Mantri, T. Morimae, A. Mizutani, and J. F. Fitzsimons: “Resource-efficient verification of quantum computing using Serfling’s bound,” npj Quantum Information，Vol．5, No．27，2019.
（2）　Y. Takeuchi, Y. Matsuzaki, K. Miyanishi, T. Sugiyama, and W. J. Munro: “Quantum remote sensing with asymmetric information gain,” Phys. Rev. A, Vol. 99，No. 2，022325，Feb. 2019.
（3）　P. Yin, Y. Takeuchi, W.-H. Zhang, Z.-Q. Yin, Y. Matsuzaki, X.-X. Peng, X.-Y. Xu, J.-S. Xu, J.-S. Tang, Z.-Q. Zhou, G. Chen, C.-F. Li, and G.-C. Guo: “Experimental Demonstration of Secure Quantum Remote Sensing,” Phys. Rev. Appl., Vol, 14, No. 1，014065，July 2020．
（4）　M. Hayashi and Y. Takeuchi: “Verifying commuting quantum computers via fidelity estimation of weighted graph states,” New J. Phys.，Vol. 21, 093060，2019.
（5）　谷・秋笛・竹内： “量子コンピュータの能力を引き出すアルゴリズムとその検証技術，”NTT技術ジャーナル，Vol. 35，No. 4，pp. 29-32，2023．
（6）　Y. Takeuchi, Y. Takahashi, T. Morimae, and S. Tani: “Divide-and-conquer verification method for noisy intermediate-scale quantum computation,” Quantum，Vol. 6, p．758，2022.
（7）　A. Mizutani, Y. Takeuchi, R. Hiromasa, Y. Aikawa, and S. Tani: “Computational self-testing for entangled magic states,” Phys. Rev. A，Vol. 106, No. 1，L010601，July 2022.