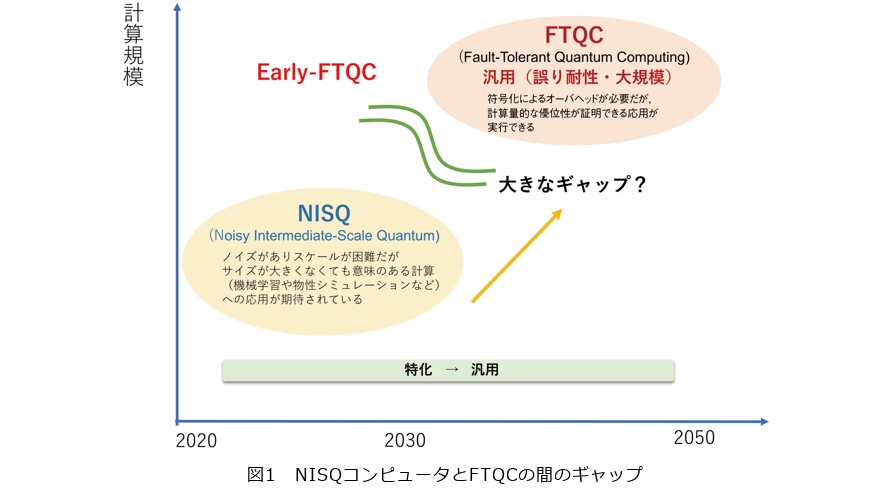
符号を用いたエラー訂正を行わないNISQ （Noisy Intermediate-Scale Quantum）コンピュータは、符号化のオーバヘッドは不要ですが、エラーがどうしても積もっていくため、計算サイズに限界があります。一方で、エラー訂正可能な誤り耐性量子コンピュータ（FTQC： Fault-Tolerant Quantum Computer）には符号化したまま計算するためのオーバヘッドがあるため、ある程度大きなサイズの量子コンピュータが必要となります。そうすると、図1のようにNISQコンピュータとFTQCの間にそのオーバヘッド量に対応するギャップが生じることになってしまいます。このギャップはどうしようもないのでしょうか。一昔前はここのギャップは仕方がないという意見も多かったのですが、最近私たちのチームは、このギャップを克服していくためのこれまでにない新しい方法を提示しました。このような動機に基づいた研究の流れは、世界的にも同時期に始まり、現在は早期誤り耐性量子計算（Early-FTQC）のように呼ばれ世界的な研究のムーブメントになっています。本稿では、誤り耐性量子コンピュータの早期実現に向けた効率化や新しい手法の取り組みを紹介します。

本特集記事『超伝導量子コンピュータのシステムの設計と開発』において、現在クラウドサービスとして動いている超伝導量子コンピュータについて紹介しました。この規模の量子コンピュータでどの程度のことが可能でしょうか。チップに載っている量子ビット数は64ビットであり、理想的な状況であれば既存の古典コンピュータによる大規模計算を持ってしてもできない計算ができるといわれています。実際にGoogleは、2019年に53量子ビットを用いて古典的にシミュレーションをすることが困難な量子的な統計効果が現れる計算を発表しました^（1）（ただし、この計算は実際に何かの役に立つ計算とは言いづらいものであり、かつ古典計算でも思っていたよりは速く計算ができるという指摘もその後複数出ました）。また、変分量子計算というNISQ時代の効率性を重視したヒューリスティックな量子計算手法により、古典コンピュータにはない量子的な状態変化が計算にうまく活かされたうえでの、高速で役に立つ計算ができる可能性があります。ただし、ここにも注意しないといけない点があり、ヒューリスティックな手法であるがゆえに、計算量的に高速になる根拠を示すことが難しい点、そして理想的でない場合の現実的なノイズやエラーの問題があります。現状の量子コンピュータが1回のゲート操作をするときに起こるエラーは0.1〜1％程度であるとされており、大まかにいうとゲート数の分だけエラーが加算されていくといえるので、エラーへの対処が何もなければ1000回のゲートを行うのもなかなか厳しい状況です。この状況でエラーへの対抗手段として現在でも用いることが可能な方法が、本特集記事『量子エラー抑制とその進展』で紹介した量子誤り抑制です。量子誤り抑制を用いると、上記のような計算がエラーに埋もれてしまうような状況に対して、量子計算を何度も実行して得られた複数の結果から、エラーを統計的に推定し、計算中に起きたエラーを修正することにより正しい計算結果を得ることができます。ただし、これはエラーが多ければ多いほど推定が困難になるため、量子計算を繰り返し実行し測定を行うコストが大きくなります。実際に、エラー数に対して指数関数的に推定が困難となっていきますので、現実的には誤り抑制できる計算規模には限界があります。ただし、2023年6月にIBMから、量子誤り抑制も巧妙に活用することで、127量子ビットの超伝導量子コンピュータを用いて古典計算でも解くのが困難な物性物理の問題を解いたという結果も発表されたように^（2）、NISQ領域において古典計算を超える有用な計算が行える可能性も引き続き追求されています（こちらについてもやはり古典的にもっと早く計算できるのではという議論も進んでいます）。

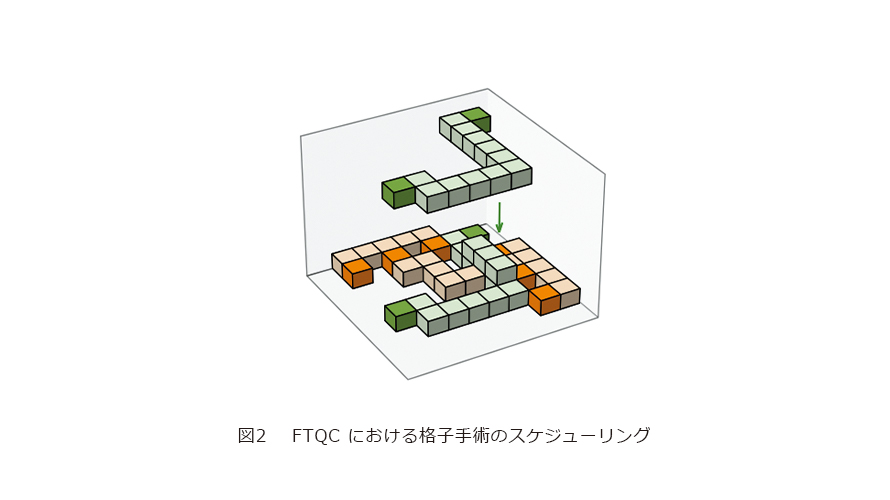
さて、それでは量子コンピュータはこのノイズやエラーを克服できず、これ以上大きくスケールすることはできないのでしょうか。これについては、量子コンピュータにも符号を用いたエラー訂正が可能であることが知られており、符号化したまま量子計算を行い続ける誤り耐性量子計算（FTQC）という手法があることが分かっています。これには符号化したまま量子計算を行うためのオーバヘッドが必要であり、必要な量子ビット数は符号化しない場合の1000〜10000倍程度ともいわれています。ただし誤り耐性量子コンピュータのアーキテクチャを考慮した符号化や復号の効率化、コンパイラの研究開発はまだ始まったばかりともいえ、今後の効率化には非常に期待がかかります。私たちはこのような効率化の研究をこれまでに複数行っており、ここではそのうち2つを紹介します。1番目は符号の処理の効率化についてです。現在、量子計算の標準的な符号は表面符号と呼ばれるもので、2次元格子状に配置した量子ビット間の近接相互作用において比較的効率的に動作し、エラー耐性しきい値も良い値が出る符号です。この符号を用いて符号化したまま量子計算を行う手法の有望なものが格子手術という手法です。これの効率化は、図2のように計算の時間軸も考慮した3次元における計算パスのスケジューリング問題になることを示し、いくつかの有望な効率化を行いました^（3）。2番目は量子アルゴリズムの回路効率化についてです。量子化学や物性物理のハミルトニアンの固有エネルギーを主要な量子アルゴリズムである量子位相推定で求めるタスクは、FTQCで実用的な問題に対し量子優位性を示す代表的なアプローチです。Qubitization^{（4）（5）}は過去の手法と比較して少ないリソースでハミルトニアンを量子位相推定可能なかたちに変換する手法です。初期のFTQCにおいて優位性のある計算の実現を早めるためには、このQubitization中の回路要素数を最適化する必要があります。本研究では、ハミルトニアンの構造を利用してFTQCにおいてコストのかかる操作であるTゲート操作の数を削減することができました。具体的にはSchwinger模型に対する回路に対して2次多項式的なTゲート数の削減に成功しました^（6）。

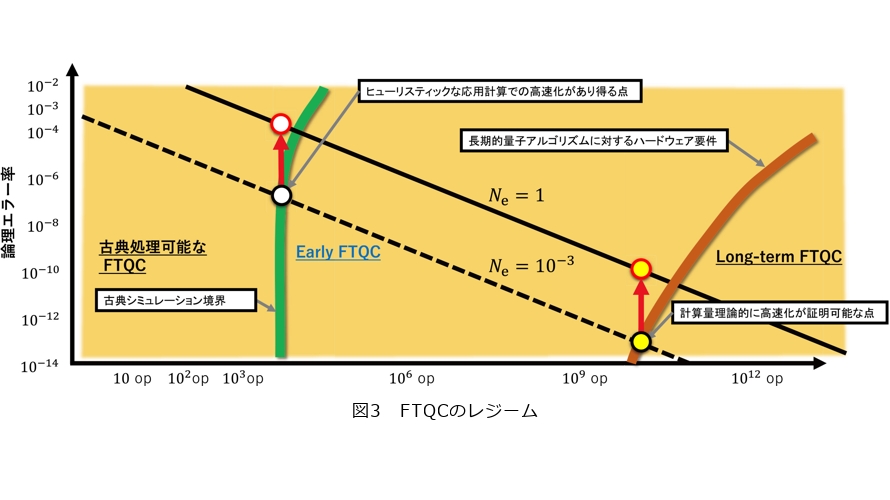
前節で、FTQCとその効率化について紹介しましたが、FTQCそのものの計算の効率化にもどこかでは限界があり、どうしてもオーバヘッドがかかることは否めません。ではどの程度から有用なFTQCは行えるようになるでしょうか。図3にFTQCのレジームを表しました。横軸は符号化された量子状態に対して行う論理的な演算回数です。符号化されたまま演算するオーバヘッド込みで1回と数えます。縦軸はその論理演算のエラー率、つまり符号化をしたにもかかわらず直しきれないエラーが論理演算ごとに起こる確率です。論理演算数が大きく、論理エラー率が小さいほど大きなFTQCを実行できます。この図の緑の線から左の領域は計算サイズが小さすぎて古典シミュレーションが可能な領域です。エラー率が大きいとさらにシミュレーションしやすくなるので上部のほうで線が曲がっています。茶色の線の右側がLong-term FTQC、ここは意味のある応用に対して量子計算の計算量的な優位性が証明できるアルゴリズムが実行できる領域で、長期的にめざすFTQC領域を指します。そして、その間が論理的な量子超越性を満たす境界からLong-term FTQCの境界までの領域であり、私たちは論文^（7）において、この領域をEarly-FTQCと呼んでいます。ここにはヒューリスティックに意義のある量子計算が存在していると考えられ、誤り耐性量子計算のもっとも初期に行われるものがこの領域に当たると考えられます。このEarly-FTQCの初めの時期に行われる量子アルゴリズムはNISQアルゴリズムと共通するようなものも多いかもしれませんが、NISQとの大きな違いは、すでに誤り耐性を獲得しているので、その後の量子コンピュータのスケールアップに応じて大きな計算が引き続き行い続けられる、つまり計算サイズが大きくなるにつれてより良い計算ができる可能性が広がっていくという点です。
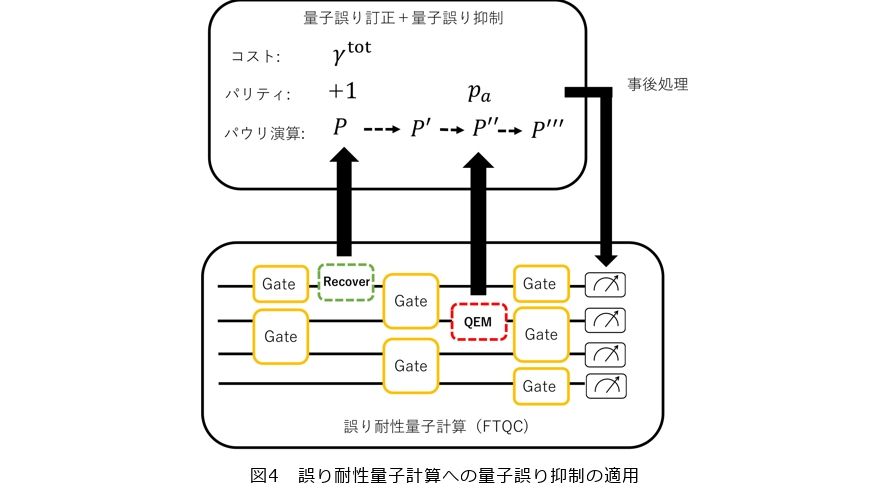
さて、この初期の誤り耐性量子計算 Early-FTQCの実現をさらに早める方法はないでしょうか。前節で説明したような効率化の手法はもちろん重要であり効果的です。ほかにも、古典計算の事後処理を追加することで量子ビット数を減らせるようにアルゴリズムの回路を書き換えるというような提案もされています^（8）。さらに私たちは、最近全く新しい手法として、これまでNISQ向けの技術だと思われてきた量子誤り抑制をFTQCに用いることが可能であることを示し、Early-FTQCの実現をさらに早められることを示しましたので、これについてここで紹介します^（7）。私たちは前述した量子誤り抑制の1つである擬確率法をFTQCに適応する方法を考案しました。NISQのときと異なり、ここでは物理エラーではなく、論理エラーの誤り抑制を行います。図4のように、FTQCにおいてはエラー訂正のためのリカバリー処理をパウリ演算という基本的な量子演算を用いて行いますが、これはシンプルな演算なため、最後の古典事後処理として一括にまとめて効率的に行えることが分かっています。擬確率法による量子誤り抑制の処理も多くの場合は同様にこのパウリ演算で行えるので、この古典事後処理に組み込むことが可能となります（パウリ演算で行えない場合もあるのですが、この場合は物理的に処理を行います。詳細は参考文献^（7）を参照）。ここで重要となってくるのは量子誤り抑制にかかるコストです。誤りの量に応じて結果の分散が広がるので、統計的に正しい結果を見積もるために計算を繰り返し行うコストがかかります。NISQコンピュータにおいては誤り訂正機能がないため、計算サイズが大きくなるにつれ誤りの量が大きくなります。量子誤り抑制にかかるコストは指数関数的に大きくなっていくので、量子誤り抑制を使えるサイズには現実的に限界が来てしまいます。FTQCにおいては、誤り訂正機能があるので、計算サイズが大きくなっても適度なパラメータにおいて常に量子誤り抑制が使える領域が存在することになります。通常FTQCにおいては、正しい結果を得るために計算結果に残るエラーの数を1より十分小さくなるように符号距離、オーバヘッドを設定しますが（図3のN_e＝10⁻³のライン）、量子誤り抑制が使えるのならば、FTQCの計算結果のエラー数を1程度にまで緩めて（図3のN_e＝1のライン）、符号距離を短く、誤り訂正のために必要なオーバヘッドを小さくすることが可能となります。図3において赤い矢印がこのことを示しており、これによりEarly-FTQCの領域が拡大していることが分かります（Long-term FTQCの領域も同様に拡大しています）。実際に量子誤り抑制を用いることでFTQCに必要な量子ビット数を80％程度削減できる場合があることを私たちは示しました。別の見方をすると、同じ量子ビット数を使うならば、誤り抑制の効果により量子演算の回数をさらに1000倍増やした大きな計算ができることを示しました。

Early-FTQCの研究はその後もさらにさまざまな意味を伴いながら進展しています。最近はさらに大きな意味合いでのEarly-FTQCも検討されています。先ほどは初期のFTQCおよびさらにその実現を早めるという意味でのEarly-FTQCでしたが、最近はまさにNISQとFTQCの間といえるような「部分的な」FTQCという意味でのEarly-FTQCの概念も登場しています。例えば、量子計算における符号化のオーバヘッドが大きいことが知られている回転ゲート部分は誤り訂正をせずに、符号化のオーバヘッドが小さいクリフォードゲートと呼ばれる回路部分を誤り訂正する部分的なFTQCが提案されています^（9）。この場合、回転ゲート部分に載るエラーが積み重なるので、これにより計算サイズの限界が決定しますが、NISQコンピュータに比べて大きな量子計算が可能になる可能性があります。私たちからも量子誤り抑制と量子誤り訂正の中間的な処理をめざすような擬似量子誤り検出という提案も行っています^（10）。これらのようにNISQとFTQCの間をつないでいくような研究開発が近年スタートしています。この間を自由に適度な誤り訂正能力を選択し、つないでいくことが可能となれば量子コンピュータのサイズが大きくなるにつれて、符号化に伴うギャップが起こることなく、常に以前より良い計算が可能となる量子コンピュータの開発を続けていくことが可能となります。そのような時代が後もう少しでやってくるのかもしれません。

■参考文献
（1） F. Arute, K. Arya, R. Babbush, D. Bacon, J. C. Bardin, R. Barends, R. Biswas, S. Boixo, F. G. S. L. Brandao, D. A. Buell, B. Burkett. Y. Chen, Z. Chen, B. Chiaro, R. Collins, W. Courtney, A. Dunsworth, E. Farhi, B. Foxen, A. Fowler, C. Gidney, M. Giustina, R. Graff, K. Guerin, S. Habegger, M. P. Harrigan, M. J. Hartmann, A. Ho, M. Hoffmann, T. Huang, T. S. Humble, S. V. Isakov, E. Jeffrey, Z. Jiang, D. Kafri, K. Kechedzhi, J. Kelly, P. V. Klimov, S. Knysh, A. Korotkov, F. Kostritsa, D. Landhuis, M. Lindmark, E. Lucero, D. Lyakh, S. Mandrà , J. R. McClean, M. McEwen, A. Megrant, X. Mi, K. Michielsen, M. Mohseni, J. Mutus, O. Naaman, M. Neeley, C. Neill, M. Y. Niu, E. Ostby, A. Petukhov, J. C. Platt, C. Quintana, E. G. Rieffel, P. Roushan, N. C. Rubin, D. Sank, K. J. Satzinger, V. Smelyanskiy, K. J. Sung, M. D. Trevithick, A. Vainsencher, B. Villalonga, T. White, Z. J. Yao, P. Yeh, A. Zalcman, H. Neven, and J. M. Martinis：“Quantum supremacy using a programmable superconducting processor, ”Nature, Vol. 574, pp.505–510, Oct. 2019.
（2）　Y. Kim, A. Eddins, S. Anand, K. X. Wei, E. van den Berg, S. Rosenblatt, H. Nayfeh, Y. Wu, M. Zaletel, K. Temme, and A. Kandala：“Evidence for the utility of quantum computing before fault tolerance, ”Nature, Vol. 618, pp.500–505, June 2023.
（3）　浜田・鈴木・徳永：“時間軸方向を活用した効率的な格子手術のスケジューリング, ”第8回 量子ソフトウェア研究会, 2023.
（4）　R. Babbush, C. Gidney, D. W. Berry, N. Wiebe, J. McClean, A. Paler, A. Fowler, and H. Neven：“Encoding electronic spectra in quantum circuits with linear t complexity,” Phys. Rev. X, Vol. 8, No. 4, 041015, 2018.
（5） G. H. Low and I. L. Chuang：“Hamiltonian simulation by qubitization,” Quantum, Vol. 3, p. 163, 2019.
（6）　小泉・鈴木・徳永：“Pauli積集合による量子位相推定回路の効率化,”第48回 量子情報技術研究会, 2023.
（7） Y. Suzuki, S. Endo, K. Fujii, and Y. Tokunaga：“Quantum Error Mitigation as a Universal Error Reduction Technique: Applications from the NISQ to the Fault-Tolerant Quantum Computing Eras,”PRX Quantum, Vol. 3, No. 1, 010345, March 2022.
（8）　L. Lin and Y. Tong：“Heisenberg-Limited Ground-State Energy Estimation for Early Fault-Tolerant Quantum Computers”, PRX Quantum, Vol. 3, No. 1, 010318, Feb. 2022.
（9）　Y. Akahoshi, K. Maruyama, H. Oshima, S. Sato, and K. Fujii：“Partially Fault-tolerant Quantum Computing Architecture with Error-corrected Clifford Gates and Space-time Efficient Analog Rotations,” arXiv:2303.13181.
（10） K. Tsubouchi, Y. Suzuki, Y. Tokunaga, N. Yoshioka, and S. Endo：“Virtual quantum error detection, ”arXiv:2302.02626.