2019年10月号
Physics & Informatics Laboratoriesの取り組み
Physics & Informatics Laboratories(NTT PHI Labs)は、量子と脳の境界領域に将来の情報処理技術に変革をもたらす新原理が存在すると考え、ここに研究領域を設定しました。特に、量子─古典クロスオーバーの物理とニューラルネットワークにおける臨界現象に着目しています。この量子と脳の境界領域で動作するコンピュータをシンプルにエレガントにそして実用的に実装する手段として、光技術、特に室温で量子効果を実現できる光パラメトリック発振器にフォーカスします。本稿では、NTT PHI Labsの研究領域を構成する概念、技術、応用先について紹介します。
山本 喜久(やまもと よしひさ)
NTT Research, Inc. NTT PHI Labs 所長
光パラメトリック発振器を用いた量子ニューラルネットワーク
コヒーレントな電磁波を発生する発振器の開発とその応用分野の開拓は、2つの異なる原理に基づく発振器の競合の歴史でもあります。2つの発振器とは、電気工学の言葉を使えば、ポンプ源のコヒーレンスを必要としない負性抵抗発振器と、コヒーレントなポンプ波を必要とする非線形リアクタンス発振器のことを指します。どの周波数帯の発振器の開発も、まず実現しやすい負性抵抗発振器が登場し、その後より雑音の少ない非線形リアクタンス発振器が開発されるという歴史をたどってきました。紫外から赤外に至る広い波長域をカバーする光の発振器の開発の歴史もまた例外ではありません。光の負性抵抗発振器であるレーザは、ヒューズ研究所のTheodore Maimanの手により1960年に実現されました(1)。一方、光の非線形リアクタンス発振器である光パラメトリック発振器(特に実用上重要な連続波を発生するもの)は、スタンフォード大学のStephen HarrisとRobert Byerにより1968年に実現されました(2)。
20世紀に花開いた光通信技術はレーザにより支えられてきましたが、21世紀の光情報処理技術は光パラメトリック発振器により支えられるであろう、というのが私たちの将来ビジョンです。光パラメトリック発振器は、発振しきい値以下のポンプ領域では量子性の強いアナログ素子として振舞い、発振しきい値以上のポンプ領域では、古典性の強いデジタル素子として振舞います。後述するように、将来の情報処理技術は、量子計算リソースと古典計算リソースの両方を同時に必要としますが、光パラメトリック発振器は室温でこの量子-古典の二面性を同時に実現しているほとんど唯一の素子です。
私たちは、光パラメトリック発振器をニューロンとするニューラルネットワークを構成し、これを用いて、現代コンピュータが不得意な組合せ最適化問題や量子多体問題を解こうとしています(3)(図1)。ニューラルネットワークを構成するもう1つの要素(シナプス結合)に関しては、特にすべてのニューロン間にシナプス結合をはる全結合型ニューラルネットワークを実現するための2つの実装方式があります(図2)。N個のニューロンにはN個の光パラメトリック発振器を使うのではなく、長さ1~10 kmの光ファイバリング共振器中を周回するN個のパラメトリック発振光パルスを用います。この方法により、欠陥のない均一なN個のニューロンが1つの共振器中に同時に実現されることになります(4),(5),(6)。
光遅延線結合方式では、(N-1)本の光遅延線と同数の光変調器でN(N-1)個のシナプス結合係数[Jij]を実装できます(4)。この方式では、各時刻に、1つのターゲットパルスiに対して(N-1)個の入力パルスjが結合係数Jijを介して同時に結合されるので、N個のターゲットパルスすべてにこのことが実現される1周回ごとにN(N-1)個のJijが実装されることになります。また、方向性を持ったシナプス結合(Jij≠Jji)が簡単に実装できるメリットを有します。
一方、測定フィードバック方式では、たった1つの測定フィードバック回路でN(N-1)個の全シナプス結合を実現できます(5),(6)。前者は大規模、高速、疎結合のニューラルネットワークの実装と量子多体問題への応用に適し、後者は中規模、高次非線形、密結合のニューラルネットワークの実装と組合せ最適化問題への応用に適すると考えています。
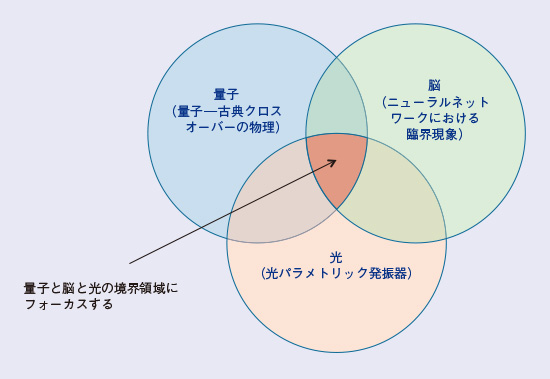
図1 NTT PHI Labsの研究領域
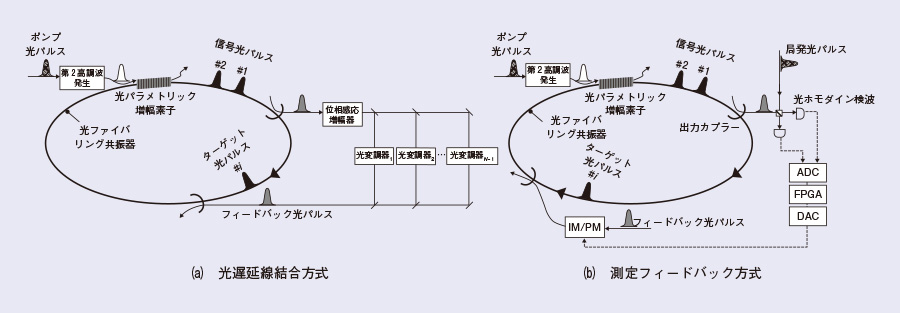
図2 光パラメトリック発振器による量子ニューラルネットワークの構成
応用分野
次に、この光パラメトリック発振器を用いた量子ニューラルネットワークの期待される応用分野について紹介します。
組合せ最適化問題
組合せ最適化問題の代表格に、イジングモデルがあります。信号光とアイドラー光の周波数が等しい縮退型光パラメトリック発振器により実装されます(3)。最近の縮退型光パラメトリック発振器ネットワークのハードウェア技術の向上とアルゴリズムの進化によって、量子ニューラルネットワークの1つであるコヒーレントイジングマシンは大幅に高性能化し、組合せ最適化問題に特化した量子コンピュータの1つである量子アニーリングマシンや最先端アルゴリズム(BLS: Breakout Local Search)を実装したノイマン型コンピュータに対して優位性を持つまでに至っています(7),(8)。さまざまな組合せ最適化問題をイジングモデルにマップして、この汎用最適化ソルバーを用いて解く時代がいずれ来ることが期待されています。具体的な問題として、創薬や生体触媒開発のためのリード最適化、無線通信ネットワークのリソース配分、圧縮センシングにおけるスパース推定、などへの応用アルゴリズム開発が行われています。
一方、連続量変数の最適化問題の代表格としてXYモデルがあります。これを解くコヒーレントXYマシンは、信号光とアイドラー光の周波数が異なる非縮退型光パラメトリック発振器ネットワークにより実装されます(9)。コヒーレントXYマシンで解ける具体的な最適化問題として、ソーシャルネットワークの診断(コミュニティ検出)やFintechにおけるポートフォリオ最適化などへの応用アルゴリズム開発が行われています 。
もう1つの組合せ最適化問題の代表格に、充足可能性(SAT: Satisfiability problem)問題があります。この問題を効率良く解くコヒーレントSATソルバーは、縮退型光パラメトリック発振器で再帰(リカレント)型ニューラルネットワークを構成することにより実現できます(10)。コヒーレントSATソルバーで解ける具体的な問題の1つに、ハードウェア検証とソフトウェア検証があります。
組合せ最適化問題をターゲットとするソルバーとして、パラメトリック発振器ネットワークによる計算に触発されて考案されたデジタル計算機が最近注目を集めています。光(あるいは超伝導)パラメトリック発振器ネットワークを実際に実現する代わりに、この系を記述する量子力学的運動方程式をFPGA(Field Programmable Gate Array)などのデジタル回路にアルゴリズムとしてプログラムし、一種の数値シミュレーションにより最適解を得る手法です(8),(11)。
量子多体問題
固体中の電子の振舞い、特に電子間に強い相互作用がある強相関電子系を精度良く効率的に数値シミュレーションするツールを開発することは、新材料の探索(Material Informatics)や新現象の発見(Topological Physics)に欠かせないものとなっています。特に、電子が2次元ポテンシャルに閉じ込められた2次元系には、通常の3次元系には存在しない新奇な量子現象が出現します。しかし、3次元系と異なり、2次元系では平均場近似に基づく数値シミュレーションが破綻するうえ、1次元系のような厳密解を得ることも困難です。そこで、対象とする2次元系の電子に対するハミルトニアンを制御しやすい別の量子系に人工的に実装し、この人工2次元量子系の振舞いを観測することを通して、対象である2次元電子系の物性を知ることが考えられてきました。いわゆる量子シミュレーションの概念です(12)。現在では、冷却原子、トラップイオン、超伝導回路などのさまざまな物理系を用いて固体中の電子物性をシミュレートする研究がさかんに行われています。
このような量子シミュレータの開発は、現在はまだ基礎研究の段階ですが、将来は、最先端デジタルコンピュータ(HPC: High Performance Computing)にさまざまな近似数値計算手法(動的あるいはクラスター平均場理論、量子モンテカルロ法、テンソルネットワーク法など)をアルゴリズムとして実装する物性物理学や量子化学の伝統的な手法との競争にさらされることになります。特に、シミュレーション精度、速度、装置の大きさ、価格、保守の容易さなどの多面的な要素が、将来技術としての生き残りを決定することになります。
私たちは伝統的な手法に対して競争力のある量子シミュレータの将来像として“光を使って電子をシミュレートする”装置を思い描いています(13)。
量子─古典クロスオーバーの物理
ミクロな世界を記述することに成功した量子論が、いつどのようにしてマクロな世界を支配する古典論に取って変わられるのか、という量子-古典クロスオーバーの問題は、量子物理学者にとってもっとも根源的なテーマです。この問題を分かりやすく理解する1つの理論モデルは、少数自由度を持つシステムが多数の(あるいは無限の)自由度を持つ環境系と結合している開放系を設定することです(14)。図3に示すように、システム内のコヒーレントな相互結合の強さに比べて、システム-環境間の散逸結合(デコヒーレンス)が小さくなるにつれて、線形重ね合わせ状態と量子相関を利用した量子並列探索や量子干渉による古典カオスの抑圧 といった量子計算リソースはその有効性を増していきます。このため、量子コンピュータは、環境への散逸結合をできるだけ小さくした領域で実現されるべきものと、従来は思われてきました。量子誤り訂正コードやトポロジカル量子コンピュータといったコンセプトは、こうした思想に沿って登場してきたものです。一方、環境への散逸結合が大きくなるにつれて、自発的対称性の破れによる最終解の非可逆的決定であるとか、選択された最終解の振幅を指数増幅して安定な古典情報として出力する、といった古典計算リソースはその有効性を増していきます。このため、人間の神経細胞の働きと仕組みを模倣する、あるいは人間の脳の思考方法から着想を得たニューロモルフィックコンピュータは、環境への散逸結合をできるだけ大きくして、システムの量子コヒーレンスを完全に除去した頑強な古典領域で実現されるべきものと、従来は思われてきました。
私たちは、量子・古典という2つの計算リソースが同時に利用できる量子-古典クロスオーバーの領域にこそ、将来のコンピュータが実現されるべきだと考えています。光パラメトリック発振器ネットワークは、ポンプレートを調整することにより、この量子-古典クロスオーバー領域を自由に行き来できるユニークなハードウェア・ソリューションです。このような考え方は、“人間の脳における高度な情報処理(意識、認知、決断といった)機能は巨大なニューラルネットワークにおける一種の相転移臨界現象に基づいている”とする最近の神経科学者の考え方(Computing at Criticality)と相通じるところがあります(15)。
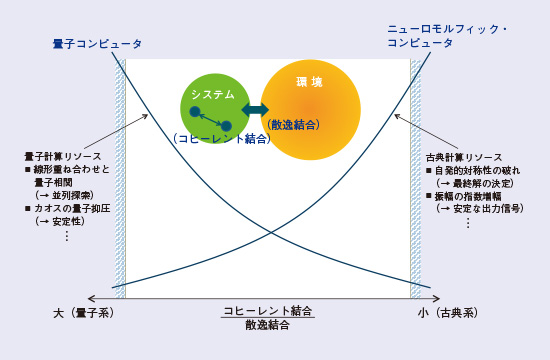
図3 量子-古典クロスオーバー領域での量子・古典計算リソース
なぜ、古典計算リソースも必要なのか?
組合せ最適化問題を量子コンピュータだけを使って解く方法を図4(a)に示します。まず、与えられた問題の解の(2N個ある)全候補を同じ確率振幅(1/√2N )を持つ線形重ね合わせ状態として表わし、次に、何らかの方法により最適解を同定し、この状態の振幅を1/√2Nから1へ増幅し、他のすべての状態の振幅を1/√2Nから0へ減衰させます。その後、N個の量子ビットに対して、0か1かの射影測定を行えば100%に近い確率で最適解が求められます。この手法のボトルネックは、最適解の振幅をどうやって増幅し、最適解でない他のすべての状態の振幅をどうやって減衰させるか、にあります。量子コンピュータを用いてこれを実現する最適な方法はGroverにより発見されています(16)。Grover iterationというこのルーチンを合計で √2N回繰り返すと、上記終状態が得られます。このことは、量子コンピュータを使って組合せ最適化問題を解こうとすると、指数時間を費やさなければならないことを意味しています。例えば、この仮想的な量子コンピュータにはデコヒーレンスもゲートエラーも全くなく、したがって量子誤り訂正をかける必要もなく、ビット間に全結合が実装され、非局在の2ビットゲートが1 nsという高速で自由に実装できると仮定し、さらに与えられた問題の最適解を何らかの方法で瞬時に同定できるとします。この理想的な量子コンピュータを用いても、最適解の確率振幅を1/√2Nから1へ増幅するためには、例えばN = 150ビットという比較的小さな問題に対しても、~200億年という長時間がかかることが示されます。
同じ問題を量子ニューラルネットワークに解かせた場合の計算時間はどの程度でしょうか。図4(b)に示すように、発振しきい値以下のN個のパラメトリック発振光パルスは0相とπ相の線形重ね合わせ状態にあるので、量子コンピュータの場合と同様、解の全候補は同じ確率振幅(1/√2N )を持つ線形重ね合わせ状態として表わすことができます。このとき、ポンプレートを発振しきい値まで上げていくと、最小のネットワーク損失を有する最適解が単一モード発振を起こし、その振幅はたかだか光子寿命(μs~msのオーダー)で初期値1/√2Nから最終値1に指数増幅されます(3)。この指数増幅は古典系(開放系)に特有な現象で、量子系では実現できません。コヒーレントイジングマシンで組合せ最適化問題の最適解を得るのにかかった計算時間(実験値)では、問題サイズN = 150ビットに対して計算時間はわずか54 msでした(7)。
この例が示していることは、隠れた周期性を持つような特殊な問題(因数分解や離散対数など)を別として、一般的な組合せ最適化問題を高速に解くための将来のコンピュータには、線形重ね合わせ状態のような量子計算リソースだけでなく、振幅の指数増幅のような古典計算リソースも欠かせない、ということです。ただし、前述のGroverの方法は必ず特定の解を増幅することが理論的に保証されていますが、量子ニューラルネットワークではその理論保証はまだ確立していません(ヒューリスティック計算機)。そのため、単純な比較はできないことに注意する必要があります。

図4 組合せ最適化問題を解く2つの方法
研究体制
NTT PHI Labsは量子力学を用いた情報処理に関する新概念・新原理の探索を行うことを目標に、外部研究機関との共同研究を積極的に進めていきます(図5)。
図5の体制図の左側に、主として実験グループをまとめました。スタンフォード大学チーム(Hideo Mabuchi教授、Martin Fejer教授、Benjamin Lev准教授、Surya Ganguli准教授、Amir Safavi-Naeini助教授)とは、光もしくは超伝導パラメトリック発振器ネットワークをベースとするコヒーレントイジングマシンやニューラルネットワーク臨界現象の研究を進めています。コーネル大学チーム(Peter McMahon助教授)とは、再帰(リカレント)型光パラメトリック発振器ネットワークをベースとするコヒーレントSATソルバーの研究を進めています。カリフォルニア工科大学チーム(Alireza Marandi助教授)とは、非縮退型光パラメトリック発振器ネットワークをベースとするコヒーレントXYマシンの研究を進めています。マサチューセッツ工科大学チーム(Dirk Englund准教授、William Oliver教授)とは、光ホモダインミキサーをベースとするコヒーレントアクセラレータ(ディープラーニングをターゲットとする)の研究を進めています。
図5の体制図の右側に、主として理論グループをまとめました。NASA Ames研究センターチーム(Eleanor Rieffel QAIL所長)とは、通信ネットワーク、スケジューリングなどの最適化応用アルゴリズムの研究を進めています。1QBitチーム(Pooya Ronaghグループ長)とは、機械学習向けの応用アルゴリズムの研究を進めています。スインバーン工科大学チーム(Peter Drummond教授、Margaret Reid教授)とは、位相空間法による量子確率微分方程式の研究を進めています。ミシガン大学(Franco Nori教授)とは、非アーベル型エニオンやトポロジカル物性の光パラメトリック発振器ネットワークによる量子シミュレーションの研究を進めています。
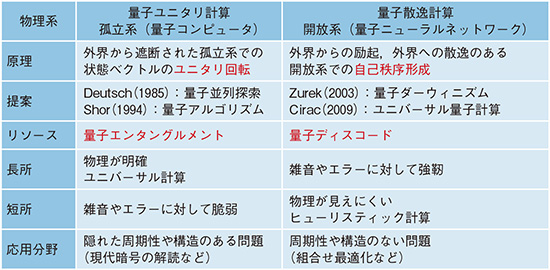
最後に、従来の量子コンピュータと私たちが研究する量子ニューラルネットワークの違いを表に示します。
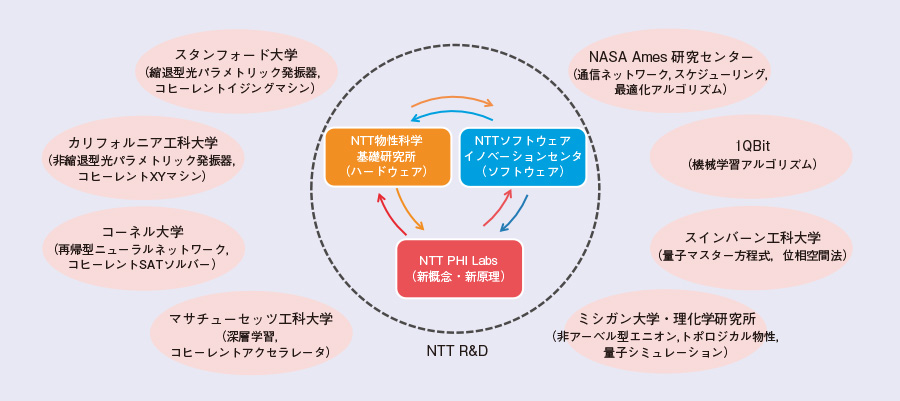
図5 NTT PHI Labsの外部共同研究機関とテーマ
表 2つの量子計算モデル
まとめ
30年以上も前のことですが、当時AT&T-NTT幹部会合なるものが両社の研究所間で毎年開催されていました。北原副社長に率いられたNTT研究所メンバの1人として、ニュージャージー州のベル研究所を訪問したときのことを思い出します。紹介されたベル研究所トップ(社長)は英国人、基礎研究担当の副社長はドイツ人、物理部門を統括するエグゼクティブディレクターはインド人でした。そして、理論物理を担当する(通称Physics 001と呼ばれていた)ディレクターは米国人でした。この方がAT&T-NTT幹部会合で基調講演を行ったときに基礎研究担当のArno Penzias副社長(1978年ノーベル物理学賞)が「そんなに早くしゃべったら、君はこの部屋の聴衆の半分を失うことになるぞ」と厳しく叱責したことが忘れられません。いつか、このようなNTT研究所をつくりたい、というのが私の夢になりました。私たちはスタートラインに立ったのです。
■参考文献
(1) T. Maiman:“Stimulated Optical Radiation in Ruby,”Nature, Vol.187, pp.493-494, August 1960.
(2) R. L. Byer, M. K. Oshman, J. F. Young, and S. E. Harris:“VISIBLE CW PARAMETRIC OSCILLATOR,”Appl. Phys. Lett., Vol.13, No.3, p.109 August 1968.
(3) Z. Wang, A. Marandi, K. Wen, R. L. Byer, and Y. Yamamoto:“Coherent Ising machine based on degenerate optical parametric oscillators,”Phys. Rev. A, Vol.88, No.6, 063853, Dec. 2013.
(4) A. Marandi, Z. Wang, K. Takata, R. L. Byer, and Y. Yamamoto:“Network of time-multiplexed optical parametric oscillators as a coherent Ising machine,”Nature Photonics, Vol.8, p.937, Oct. 2014.
(5) T. Inagaki, Y. Haribara, K. Igarashi, T. Sonobe, S. Tamate, T. Honjo, A. Marandi, P. L. McMahon, T. Umeki, K. Enbutsu, O. Tadanaga, H. Takenouchi, K. Aihara, K. Kawarabayashi, K. Inoue, S. Utsunomiya, and H. Takesue:“A coherent Ising machine for 2000-node optimization problems,”Science, Vol.354, No.6312, pp.603-606, Nov. 2016.
(6) P. L. McMahon, A. Marandi, Y. Haribara, R. Hamerly, C. Langrock, S. Tamate, T. Inagaki, H. Takesue, S. Utsunomiya, K. Aihara, R. L. Byer, M. M. Fejer, H. Mabuchi, and Y. Yamamoto:“A fully programmable 100-spin coherent Ising machine with all-to-all connections,”Science, Vol.354, No.6312, pp.614-617, Nov. 2016.
(7) R. Hamerly, T. Inagaki, P. L. McMahon, D. Venturelli, A. Marandi, T. Onodera, E. Ng, C. Langrock, K. Inaba, T. Honjo, K. Enbutsu, T. Umeki, R. Kasahara, S. Utsunomiya, S. Kako, K. Kawarabayashi, R. L. Byer, M. M. Fejer, H. Mabuchi, D. Englund, E. Rieffel, H. Takesue, and Y. Yamamoto:“Experimental investigation of performance differences between coherent Ising machines and a quantum annealer,”Science Advances, Vol.5, No.5, eaau0823, May 2019.
(8) T. Leleu, Y. Yamamoto, P. L. McMahon, and K. Aihara:“Destabilization of Local Minima in Analog Spin Systems by Correction of Amplitude Heterogeneity,”Phys. Rev. Lett., Vol.122, No.4, 040607, Feb. 2019.
(9) Y. Takeda, S. Tamate, Y. Yamamoto, H. Takesue, T. Inagaki, and S. Utsunomiya:“Boltzmann sampling for an XY model using a non-degenerate optical parametric oscillator network,”Quantum Sci.Technol., Vol.3, No.1, 014004, Nov. 2017.
(10) M. Ercsey-Ravasz and Z. Toroczkai:“Optimization hardness as transient chaos in an analog approach to constraint satisfaction,”Nature Physics, Vol.7, pp.966-970, Oct. 2011.
(11) H. Goto, K. Tatsumura, and A.R.Dixon:“Combinatorial optimization by simulating adiabatic bifurcations in nonlinear Hamiltonian systems,”Science Advances, Vol.5, eaav2372, April 2019.
(12) R. P. Feynman:“Simulating physics with computers,”Int. J. Theoretical Physics, Vol.21, pp.467-488, June 1982.
(13) M. D. Fraser S. Höfling, and Y. Yamamoto:“Physics and applications of exciton-polariton lasers,”Nature Materials, Vol.15, pp.1049-1052, Sept. 2016.
(14) W. H. Zurek:“Decoherence, einselection, and the quantum origins of the classical,”Rev. Mod. Phys., Vol.75, No.3, pp.715-775, July 2003.
(15) J. Beggs:“Editorial: Can There Be a Physics of the Brain?,”Phys. Rev. Lett., Vol.114, 220001, June 2015.
(16) L. K. Grover:“A fast quantum mechanical algorithm for database search,”Proc.of 28th Annual ACM Symposium on the Theory of Computing, pp.212-219, 1996.

山本 喜久
問い合わせ先
NTT Research, Inc.
NTT PHI Labs
E-mail info@ntt-research.com





レーザのコヒーレンスを通信に応用するコヒーレント光通信の研究がNTT基礎研究所で始まったのは1979年のことでした。40年の歳月を経て、光パラメトリック発振器のコヒーレンスを情報処理へ応用する量子ニューラルネットワークの研究をスタートできるまで、光技術は進歩をとげてきました。