2019年11月号
イジング型計算機による組合せ最適化のためのハイブリッド計算基盤
- LASOLV®
- 組合せ最適化
- 組合せ最適化非ノイマン型計算機
LASOLV®はNTTが研究開発に取り組む、新しい原理に基づいた計算装置です。LASOLV®は組合せ最適化問題を極めて高速に解くことが可能であるため、これまでは解くことができなかった課題の解決が期待されています。一方で実世界の問題をLASOLV®で解くためには、LASOLV®が受け付ける形式への問題変換や、従来からあるデジタル計算機との連携などの課題があります。本稿では、このような課題の解決手段を幅広いユーザに提供し、LASOLV®の効果的な利用を可能にするLASOLV®計算システムを紹介します。
新井 淳也(あらい じゅんや)/ 八木 哲志(やぎ さとし)/ 内山 寛之(うちやま ひろゆき)/ 富田 均也(とみた きんや)/ 宮原 和大(みやはら かずひろ)/ 巴 徳瑪(ともえ とくま)/ 堀川 桂太郎(ほりかわ けいたろう)
NTTソフトウェアイノベーションセンタ
イジング型計算機の利用における課題
イジング型計算機の利用における課題
ムーアの法則の終焉に伴い、計算機の性能を飛躍的に向上させるのは困難になりつつあります。一方で、私たちは今日のデジタル計算機を圧倒するような複雑な問題に依然として直面しています。組合せ最適化問題はそのような問題の1つです。基礎的な組合せ最適化問題としては、指定された複数の都市をもっとも効率的にめぐる訪問順を求める問題(巡回セールスマン問題)や、限られた色数で隣り合う領域が異なる色になるように塗り分ける問題(グラフ彩色問題)が有名です。
これらの応用の一例としては無線通信の品質改善があります。複数の無線アクセスポイントをイベント会場に配置する際、近傍のアクセスポイントが互いに同じ周波数帯を使用していると、電波の干渉により通信が不安定になります。ここでグラフ彩色問題を応用することで、近傍のアクセスポイントがそれぞれ異なる周波数帯となるような割り当て方を求めることができます。このように、組合せ最適化問題は実世界の課題に広く内包されています。
組合せ最適化のさまざまな問題は、イジングモデルの基底状態探索(イジング最適化)問題に変換可能であることが知られています。イジングモデルとはスピンのネットワークを表現した統計力学のモデルです(図1)。スピンσiはアップ(+1)またはダウン(-1)のいずれかの状態をとります。Jijとhiがそれぞれスピン間相互作用と磁場の強さを表すとすると、基底状態とは次式で定義されるイジングハミルトニアンHが最小化された状態を指します。基底状態を満たすスピンの組合せが、基底状態探索問題の解となります。
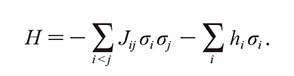
イジング最適化問題、ひいては組合せ最適化問題を効率的に解くため、D-Wave Systemsの量子アニーリングマシンや富士通のデジタルアニーラのようにイジング最適化に特化した計算機が開発されています。本稿ではそのような計算機をイジング型計算機と呼称します。NTTもまたNTT物性科学基礎研究所において光を用いたイジング型計算機であるLASOLV®の研究開発を行っています(図2)。これらの計算機の機能は限られた規模のイジング最適化問題を解くことのみですが、イジング型計算機とデジタル計算機を協調的に利用するハイブリッドアルゴリズムの使用により複雑な問題も解くことができます。例えば、大規模なイジング最適化問題を解くため、デジタル計算機上で小規模な部分問題に分解したうえで、個々の部分問題をイジング型計算機で解くという処理を繰り返す発見的手法が存在します。そのため、イジング型計算機は実世界の問題に幅広く適用可能です。
しかし、イジング型計算機の利用にあたってはいくつかの課題があります。例えば、コストや設置場所の問題で多数のイジング型計算機を用意することは困難であるため、複数人で少数のイジング型計算機を共用する仕組みが必要です。そこでいくつかの企業は、クラウドプラットフォーム上のリモートな計算資源としてイジング型計算機を提供しています(1)、(2)。プラットフォームの利用者は手元のデジタル計算機でプログラムを実行し、そのプログラムからWeb API(Application Programming Interface)リクエストを発行することでイジング最適化をそのプラットフォームに任せる(オフロードする)ことができます。ところが、イジング型計算機は1ミリ秒オーダーの時間で問題を解くため、相対的にインターネット経由の通信はあまりにも低速です。特に、ハイブリッドアルゴリズムはイジング型計算機とデジタル計算機の間で頻繁に情報をやり取りするため、通信コストによる性能低下が顕著になります。このように、イジング型計算機の利用には依然として課題があります。
これらの課題を解決すべく、NTTソフトウェアイノベーションセンタでは、LASOLV®を簡単かつ効率的に利用するためのプラットフォームの研究開発に取り組んでいます。本稿ではまず、イジング計算プラットフォームに求められる設計上のポイントを整理し、さらにそれらの要求に対する回答として私たちのプラットフォームであるLCS(LASOLV® Computing System:LASOLV®計算システム)を紹介します。LCSの大きな特徴は、利用者によって定義されたハイブリッドアルゴリズムをLASOLV®と併置されたデジタル計算機上で実行することです。これによりLASOLV®とデジタル計算機の間で効率的な通信が可能となります。さらに、LCSは幅広いユースケースにおいてイジング最適化問題への変換を容易にするライブラリを備えています。以降ではこれらについて詳しく説明します。
なお、LASOLV®は以前「量子ニューラルネットワーク」と呼ばれていました。紙面の都合でLASOLV®自体については説明しませんので、詳しくは過去の特集記事(3)を参照ください。
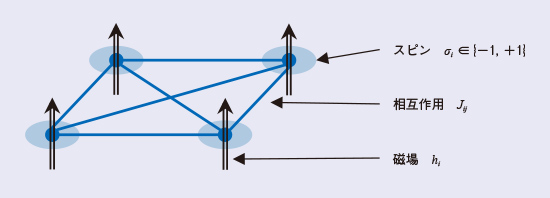
図1 イジングモデル

図2 LASOLV®外観
プラットフォーム設計における要求
次にイジング計算プラットフォームに求められる設計上の観点を3つ取り上げて説明します。
効率性
前述したように、インターネット経由の通信はイジング最適化と比較して桁違いに長い時間を要します。さらに、技術の進歩に伴いイジング型計算機が対応するスピン数は増加します。例えばLASOLV®は現状で最大2000スピンに対応していますが、NTT物性科学基礎研究所ではこれを10万スピンまで増加させることをめざしています。その結果、イジング最適化問題の規模、すなわちJijとhiのサイズはますます増大し、通信効率が性能により大きな影響を及ぼすようになります。したがって、プラットフォームは通信のオーバーヘッドが最小化されるように設計されなければなりません。
拡張性
イジング型計算機は進化の途上にあります。そのため、新しい世代のハードウェアは従来と異なる仕様を持つ可能性があり、必然的にプラットフォームはヘテロジニアス(異種混在)な計算資源を含むことになります。計算資源の使い分けは利用の複雑さを増加させるため、これらの資源を効果的かつ利用しやすい形態で提供する工夫が必要です。
生産性
各種の組合せ最適化問題をイジング最適化問題へ変換する作業は特殊な技能を要します。一方で、変換の方法はあまりにも多様であるため、それぞれの組合せ最適化問題に対応する変換アルゴリズムの提供は非現実的です。幅広い利用目的において高い生産性を実現する、利便性と汎用性を兼ね備えたプログラミングインタフェースが求められます。
LASOLV®計算システム
NTTソフトウェアイノベーションセンタでは、LASOLV®のための計算プラットフォームとしてLCSの開発に取り組んでいます。具体的には、LCSは独自のPythonライブラリ、およびジョブスケジューラなどのミドルウェアを備えた計算機クラスタです。前述した設計上の要求を満たすため、LCSは次の3つの特徴を持ちます。
LASOLV®とデジタル計算機の統合
LASOLV®とデジタル計算機の間の効率的な通信を可能にするため、LASOLV®とデジタル計算機はLCSにおいて1つのクラスタに統合されています(図3)。LASOLV®が含まれることを除けば、HPC(High-Performance Computing:高性能計算)分野において標準的なクラスタの構成です。利用者はSSH接続によるコマンド操作、またはブラウザ上のJupyter Notebookからプログラムの実行をジョブとして投入することができます*(図4)。ジョブスケジューラとライブラリの協調により、プログラムのうちデジタル計算機を使用する部分は計算ノードで実行され、イジング最適化はLASOLV®にオフロードされます(図5)。計算ノードとLASOLV®の間の通信はクラスタ内に閉じるため、インターネットに比べて広帯域・低遅延の通信が可能です。また、CPUコアおよびLASOLV®を複数のジョブが同時に使用することがないように実行されるため、複数ユーザの同時使用が可能です。
*現時点ではNotebook全体が一括でジョブ実行されます。今後の改良でインタラクティブな実行もサポートする予定です。
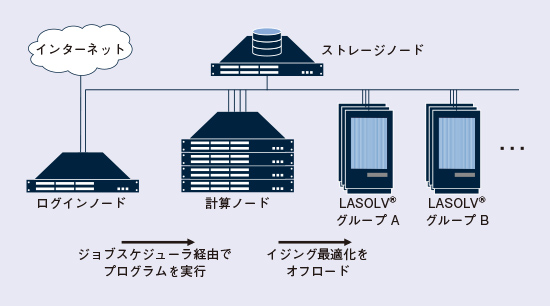
図3 LCSの構成
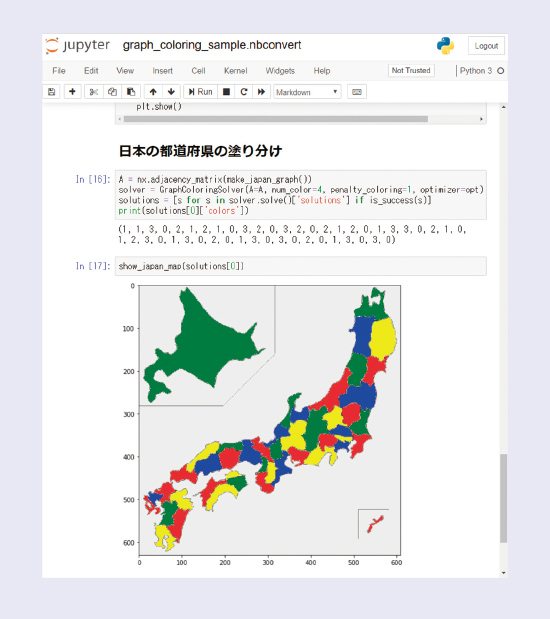
図4 Jupyter Notebookの利用イメージ
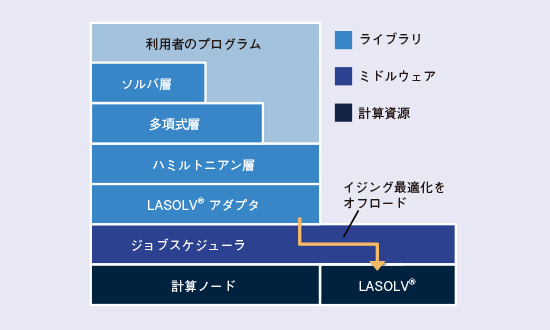
図5 LCSスタック
グループディスパッチ
LCSはスケールアウト可能な設計となっています。今後異なる仕様を持つLASOLV®が登場し得ることから、それらを管理しやすくするためLCSは互換性のあるLASOLV®をグループとして管理します。利用者はイジング最適化のオフロード先をグループ単位で指定することが可能です(図5)。ジョブスケジューラはそのグループ内で処理を振り分けることにより負荷を分散し、効果的にLASOLV®を使用します。なお、与えられたイジング最適化問題の性質(スピン数など)に基づいて必要な仕様を満たすグループを自動的に決定する機能も将来的に実装される予定です。
階層的な問題変換
利用者は次の3層からなるプログラミングインタフェースを用途に応じて使い分けることができます。
① ソルバ層:巡回セールスマン問題やグラフ彩色問題のような広く知られたNP困難問題を多項式、またはイジング最適化問題として表現された目的関数へ変換するアルゴリズム群
② 多項式層:多項式として表現された目的関数をイジング最適化問題へ変換するための内部DSL(domain-specific language:ドメイン特化言語)
③ ハミルトニアン層:イジング最適化問題(Jijとhi)を直接入力する生のインタフェース
この3段階は、手でイジング最適化問題へ変換する場合において一般的なプロセスに対応しています。すなわち、形式的な問題定義、多項式関数の最小化問題への変換、イジングハミルトニアンへの変形です。多項式層は解こうとする問題にソルバ層の実装が適さなかった場合や、手動でチューニングを行うための柔軟性が必要となる場合に有用です。例として、グラフGに含まれるn個の頂点を、隣接頂点がそれぞれ異なる色になるようにc色で塗り分けるグラフ彩色問題を考えます。AをGの隣接行列、pをハイパーパラメータとし、変数xv,i∈{0, 1}を用いると、グラフ彩色問題は次式の最小化問題に変換されます(4)。
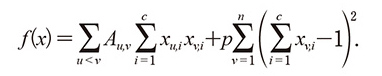
この式を展開すると変数xv,iに関する多項式が導出されますが、多項式層のDSLを用いるとPythonプログラマにとって直感的な記述でこの問題を解くことができます(図6)。
また、ハミルトニアン層はLASOLV®が対応するスピン数を超えて大規模なイジング最適化問題を解くためのハイブリッドアルゴリズムを搭載しています。これはいくつかの既存手法を基に新しく開発された発見的手法です。このような研究開発の成果を素早く利用者に届けるために私たちは独自のライブラリを開発しており、ユーザはこのライブラリで動作するプログラムを実装するだけで成果を利用可能です。
なお、他のイジング計算ライブラリ(5),(6),(7),(8)でイジング最適化問題へ変換し、LCSライブラリのハミルトニアン層に直接入力することで問題を解くという使い方も容易に実現できます。したがって利用者の自由を制限することはありません。また逆にLCSライブラリの機能の多くは汎用性があるので、イジング最適化問題への変換結果をLASOLV®以外のイジング型計算機の入力として使用することも可能です。

図6 多項式層のサンプルコード
今後の展開
本稿ではまずプラットフォームの設計における要求事項を整理し、さらにLCSがそれらをどのように達成したかを紹介しました。
現在、LCSは各種機能を兼務するハイエンドサーバ2台とLASOLV®1台を中心とするスモールスタートの構成で共同研究者に提供されています。LASOLV®を用いた研究開発を推進するため、私たちは利用状況とフィードバックに基づくLCSの評価と改良を継続的に実施していきます。
■参考文献
(1) https://cloud.dwavesys.com/leap/
(2) https://www.fujitsu.com/global/digitalannealer/services/
(3) 武居・稲垣・稲葉・本庄:“複雑な組合せ最適化問題を解く量子ニューラルネットワーク、”NTT技術ジャーナル、Vol.29, No.5, pp.11-14, 2017。
(4) A。Lucas:“Ising formulations of many NP problems、”Frontiers in Physics, Vol.2, No.5, pp.1-15, 2014。
(5) https://github.com/Blueqat/Wildqat/
(6) https://ocean.dwavesys.com/
(7) https://github.com/OpenJij/
(8) https://github.com/recruit-communications/pyqubo/

(後列左から)富田 均也/巴 徳瑪/新井 淳也/内山 寛之
(前列左から)八木 哲志/堀川 桂太郎/宮原 和大
問い合わせ先
NTTソフトウェアイノベーションセンタ
分散処理基盤技術プロジェクト
TEL 0422-59-6011
FAX 0422-59-3739
E-mail sic-lasolv-p-ml@hco.ntt.co.jp




CPUとGPUの併用と同じように、LASOLV®のような新原理に基づく計算機と従来型のデジタル計算機という視点でも適材適所の併用が重要になりつつあります。そのような研究の一助となるよう、引き続きLCSの改良に取り組みます。