2021年11月号
特集
最適化問題解決の未来:コヒーレントイジングマシン(CIM)
- コヒーレントイジングマシン
- 最適化問題
- 光パラメトリック発振器
本稿では、最適化問題の新しいソルバーとして注目されているコヒーレントイジングマシン(CIM)の動作原理とその性能評価について紹介します。レーザではなく光パラメトリック発振器を用いたCIMでは、単一光子対(2個の光子が対を成した状態)が全光パルスに同時に存在し、単一光子対レベルの微弱光で干渉計を構成します。このマシンは、誤り訂正機能を持たせることにより、既存のアルゴリズムに競合できる性能を獲得できます。
山本 喜久(やまもと よしひさ)
NTT Research, Inc. Physics and Informatics Lab 所長
はじめに
既存のコンピューティングの限界を克服するために、さまざまな新しいアプローチが模索されています。その1つに、アナログ、デジタル、あるいは古典、量子を組み合わせたハイブリッド型計算機が代替モデルとして研究されています。対象としている課題は一般にNP困難問題、NP完全問題に分類され、その1つに組合せ最適化問題があります。組合せ最適化問題を解くために、いくつかの新しいコンピューティングモデルが登場しています。例えば、量子断熱計算(または量子アニーリング)やコヒーレントイジングマシン(CIM)などです。これらの物理モデルに発想を得た新しいデジタルアルゴリズムも提案されています。NTT物性科学基礎研究所は大規模なCIMプロトタイプを開発しており、NTT Research, Inc. Physics and Informatics(PHI)Labは、このCIMの基本原理の解明に取り組んでいます。本稿では、PHI Labにおける、これまでの成果、今後の課題について解説します。
用語の定義
CIMアプローチを理解するために、いくつかの用語を定義しましょう。まずは「イジング」という用語、次に「コヒーレント」という用語を定義します。「エルンスト・イジング(Ernst Ising)」は、ドイツの物理学者で、1920年代に磁性体を説明するのために1つの数学モデルを提案した人物です。
イジングモデルは、N個の原子スピンの磁気モーメントを表す離散変数の1次元ベクトルで構成されており、それぞれ2つの状態(+1または−1)を取ります。エネルギーがもっとも低い状態である基底状態を明らかにすることと組合せ最適化問題の解を見つけることは等価です。スピン-スピン結合構成が単純ではない非プレーナグラフの場合、イジングモデルの基底状態を明らかにする作業は、計算量理論でいうところのNP困難問題に分類されます。
CIMの動作でもっとも重要な構成要素は、光パラメトリック発振器(OPO)です。インコヒーレント光(位相がランダムな雑音光)を種とするレーザの発明から5年後、1965年に初めて実現されたOPOは位相のそろったコヒーレント光を種とする発振器です。発振しきい値以下でスクイーズド状態と呼ばれる最小不確定状態を発するため、発振しきい値以下で熱雑音光を発生するレーザとは区別されます。CIMは、N × Nの結合マトリクスを通じて実世界の組合せ最適化問題にマッピングできます。その解は、エネルギーを最小化する基底状態に対応します。
このシステムは二重にコヒーレントです。つまり、2ωの周波数を持つポンプ光から1つの光子が消去されると、周波数ωの信号光で2つの光子からなる光子対が生成されます。CIMが2つのOPOで構成される場合は、1つの光子対が2つのOPOに線形重ね合わせ状態として同時に存在します。CIMがN個のOPOで構成される場合、1つの光子対がN個のOPOに線形重ね合わせ状態として同時に存在します。つまり、CIMの基本励起(単一光子対)は、N個のOPOで構成されるマシン全体にコヒーレントに広がっています。
また、それぞれのOPOパルスは、ゼロ光子(真空状態)と2光子の2つの状態にまたがって同時に存在します。このコヒーレントな重ね合わせの性質により、それぞれのOPOパルスはゼロ相(ダウンスピン)とπ相(アップスピン)の状態を同時に表現します。このように、2N個の直交状態の線形重ね合わせが、CIMでは自然に生成されます(1)(図1)。
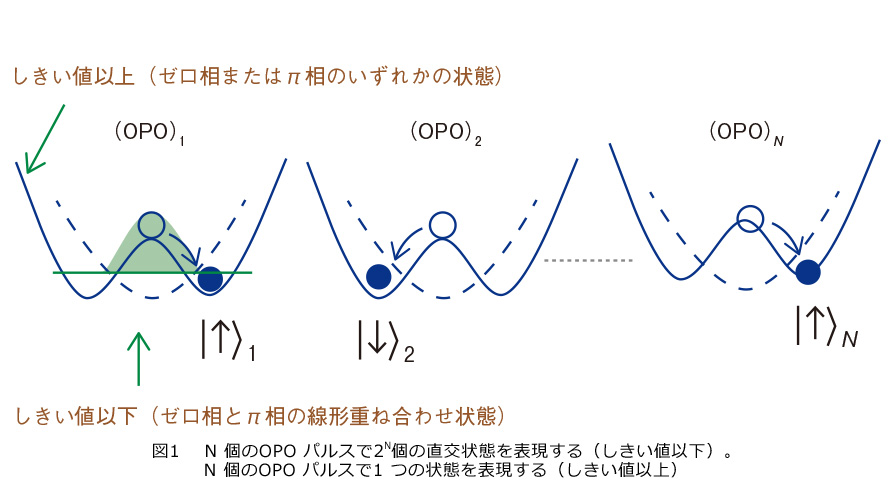
2つのCIMタイプ
実際には、2つのCIMタイプがあります。1つはエラー訂正機能を持つタイプ(closed-loop CIM)、もう1つはエラー訂正機能を持たないタイプ(open-loop CIM)です。前述したように、OPOはポンプ光から1つの光子を吸収し、2つの光子を同時にN個のパルスに放出します。それぞれのパルスで、ゼロ光子状態と2光子状態の間で干渉が起こり、量子ゆらぎが延伸されたスクイーズド真空状態になります。これがアップスピンとダウンスピンの線形重ね合わせ状態に相当します。ポンプ光がさらに大きくなると、延伸された量子ゆらぎが正の振幅と負の振幅を持ついずれかの状態に遷移します。
この分岐点が、量子系から古典系への転移点になります。しきい値未満の量子領域では、アップスピンとダウンスピンの線形重ね合わせ状態により量子並列探索が行われ、しきい値以上の古典領域では、アップスピンもしくはダウンスピンのいずれかが選択されます。この分岐点が、CIMを量子から古典へと変えるポイントであり、CIMの計算リソースの大半は、この量子-古典遷移に伴って出現します(2)。
closed-loop CIMの場合は、各OPOの振幅を一定に保つためのエラー訂正機能が付与されており、これによりマシンは局所最適解にトラップされることなく、イジングモデルの最適解を探索し続けます。マシンは1つの最適解に到達しても、そこで安定になるのではなく、別の最適解を求めて再び探索を始めます(3)。
Open-loop CIMでは、そのようなエラー訂正機能はなく、マシンは局所最適解にトラップされ、そこで安定になります。このため、短い時間で計算を切り上げ、何回も同じ問題をマシンに解かせる必要があります。
2つのマシンには、歴史やトレードオフによる違いがあります。CIMは、当初はopen-loop方式が一般的でしたが、最近はclosed-loop方式が主体になっています。closed-loopのほうが実装は困難ですが、既存のアルゴリズムを“凌駕”する性能が得られます。
CIMのパフォーマンス
CIMはこれまでどのようなパフォーマンスを発揮してきたのでしょうか。代表的な数値シミュレーションの結果を紹介します。
理想的な量子コンピュータ(QC)との比較では、closed-loop CIMはQCよりも優れた性能を発揮しています。このベンチマークでは、理想的なQCは、デコヒーレンス、エネルギー散逸、ゲートエラーは一切なく、全量子ビット間に1nsのゲート時間で遠隔結合が実現されていると仮定しています。これは現実にはあり得ない仮定ですが、それでも、(離散)断熱量子コンピューティング(dAQC)アルゴリズムやグローバー検索アルゴリズムという代表的な2種類のアルゴリズムを用いたQCの計算時間(Time to Solution: TTS)は、現実的なCIMのTTSに比べて何桁も大きな値になります。現時点でのシミュレーション結果によると、グローバーおよびdAQCアルゴリズムを用いたQCのTTSは、問題サイズnの指数に応じて増加しますが、CIMのTTSは、n½からn⅓の指数に応じて増加します。
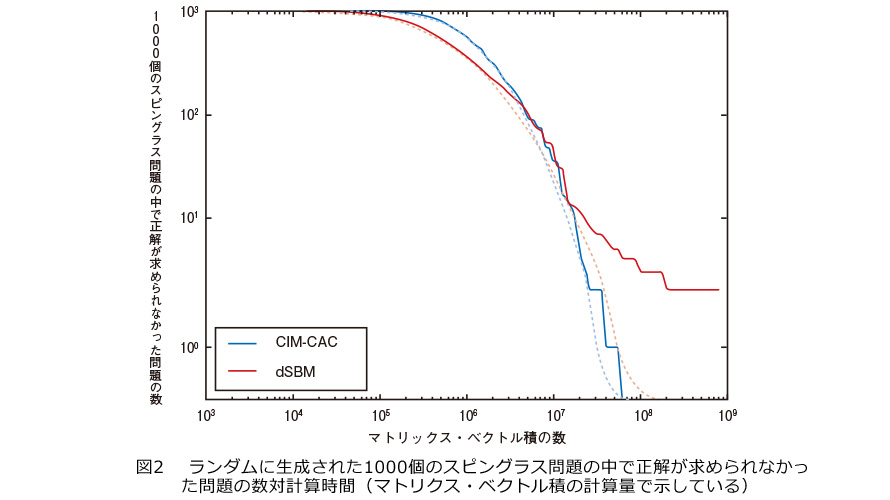
CIMはdiscrete Simulated Bifurcation Machine(dSBM)というデジタルアルゴリズムとの比較においてもある計算条件において優れた性能を示しました(図2)。dSBMは易しい問題に関しては、CIMよりも高速に解を求めることができますが、難しい問題に対しては、TTSが非常に長くなるという欠点を持ちます(4)。CIMは、またBreakout Local Search (BLS)という既存のアルゴリズムに対しても同様の優位性を持つことが分かっています(3)。
今後の研究計画
CIMの研究では、実験や数値シミュレーションによる性能評価が先行し、理論的な観点からそのパフォーマンスを理解するにはまだ多くの課題が残っています。この状況は、実験やシミュレーションによる評価が理論に対して大きく遅れているQC分野の一般的なシナリオとは対照的です。
この理論研究の遅れを解消するために、NTT Research, Inc.は、スタンフォード大学、カリフォルニア工科大学、シカゴ大学、コーネル大学、ハーバード大学、ミシガン大学、マサチューセッツ工科大学、NASA Ames研究センター、ノートルダム大学、スインバーン大学、東京工業大学、東京大学、ウォータールー大学、1QBitという14の機関との長期にわたるコラボレーションを開始しました。26人の代表研究者(Principal Investigator: PI)とともに推進するこの共同研究プロジェクトでは、量子光学および量子情報、ニューラルネットワークと脳科学、非線形フォトニクス、機械学習など、さまざまなトピックが対象になります。
スケジューリング、創薬、ワイヤレス通信、金融、回路設計、圧縮センシング、機械学習などの分野で、CIMが解決できると期待される差し迫った現実的な問題があります。さらに、この研究から派生する学際的な視点は、新たな研究分野に発展する可能性があります。物理学と神経科学の接点は、こうした知識の中でもっとも重要な分野の1つになるでしょう。
■参考文献
(1) Y. Yamamoto, T. Leleu, S. Ganguli, and H. Mabuchi: “Coherent Ising machines—Quantum optics and neural network Perspectives,” Appl. Phys. Lett., Vol. 117, No.16, 160501, Oct. 2020.
(2) Y. Inui and Y. Yamamoto: “Entanglement and quantum discord in optically coupled coherent Ising machines,” Phys. Rev. A, Vol. 102, No. 6, 062419, Dec. 2020.
(3) S. Kako, T. Leleu, Y. Inui, F. Khoyratee, S. Reifenstein, and Y. Yamamoto:“Coherent Ising Machines with Error Correction Feedback,” Adv. Quant. Technol., Vol. 3, No.11, 2000045, Nov. 2020.
(4) S. Reifenstein, S. Kako, F. Khoyratee, T. Leleu, and Y. Yamamoto :“Coherent Ising Machines with Optical Error Correction Circuits,” Adv. Quant. Technol., Vol. 4, No. 9, 2100077, Sept. 2021.

山本 喜久







CIMには、幸いなことに強力なライバルがハード技術にもアルゴリズムにもたくさんいます。これらの競合技術とのオープンな競争の中で、理解を深め、技術を磨き、結果として新しいコンピュータ技術を実現していけるものと期待しています。