膨大な選択肢からもっとも良いものを探す組み合わせ最適化問題は、現在のコンピュータでも多くの計算時間を必要とする難問です。例えば、指定された複数の訪問先をもっとも効率的に巡る順番を求める「巡回セールス問題」や、限られた色数という制約の下、与えられた地図の隣り合う領域が違う色で塗分けられるようにする「グラフ彩色問題」などは、規模が拡大するほど難しくなる典型的な組み合わせ最適化問題です。
この課題に対し、磁性体の性質を表すモデルを用いて解くという新しいアプローチで解を導き出す「イジングマシン」の研究が進んでいます。イジングマシンは、組み合わせ最適化問題の1つ、イジングモデル基底状態探索問題を解くことに特化したコンピュータです。イジングモデルとは、磁石（スピン）のネットワークを表現した統計力学のモデルです（図1）。スピンσ_iはアップ（+1）またはダウン（−1）のいずれかの状態をとります。J_ijとh_iがそれぞれスピン間相互作用と磁場の強さを表すとすると、基底状態とは次式で定義される二次多項式のイジングモデルHが最小化された状態を指します。基底状態を満たすスピンの組み合わせが、基底状態探索問題の解となります。

組み合わせ最適化問題はさまざまな種類がありますが、このイジングモデル基底状態探索問題に変換可能であることが理論的に証明されています。そのため、D-Wave Systems^（1）や富士通^（2）などのさまざまな会社がイジングマシンを開発し、それを用いていろいろな組み合わせ最適化問題を解く取り組みを進めています。NTT研究所においても、レーザ光を利用したコヒーレントイジングマシン^（3）「LASOLV^®」を開発しています。

イジングマシンの活用にあたっては、前述のとおり解こうとする問題をイジングマシンに入力可能なイジングモデルと呼ばれる形式で表現する必要があります。そして、問題をイジングモデルで表現する際には、スピンの取る±1の値と問題の解の意味との間に対応付けを行い、イジングモデルの値が最小となるときが得たい解に対応するように多項式をつくる必要があります。最小となるときと得たい解を対応付けるのは、イジングマシンが入力されたイジングモデルを最小化するようなスピンの値を求める計算機であるためです。このイジングモデルの考案作業は問題の複雑さに比例して煩雑になり、イジングマシン利用の難易度を上げてしまいます。NTTコンピュータ＆データサイエンス研究所では、このイジングモデルの考案作業を大きく簡略化する機能を持つSDK（Software Development Kit）「cimsdk」の開発をしています。まずは通常のイジングモデルの考案作業を簡単な問題を例に説明します。
あなたは自部署のスタッフ6人（仮にA、B、C、D、E、Fとします。）に6つのデスク（仮にU、V、W、X、Y、Zとします。）を割り当てることを考えています。6つのデスクは図2（a）のような位置関係です。スタッフ1人につきデスクは1つ割り当てる必要があります（前提1）。また、AさんとBさん、CさんとDさんとEさんとFさんは同一業務でチームを組んでいるので、隣接するデスクであることが望ましいです。ここでは同チームで隣接デスクとなったスタッフの組み合わせ1つごとに1点加算され、この点数を最大化することをめざします（前提2）。
この前提1、前提2を踏まえると、図2（b）のような割当てが最大点数となる解の1つです。この例題について、イジングモデルによる表現を考えていきます。
まず、±1のスピンと問題の解の意味の間の対応付けを考えます。今回はスタッフ6人とデスク6つの組み合わせ36通りについて1つずつスピンを用意し、「+1であればそのスタッフがそのデスクに割り当てられた、−1であれば割り当てられなかった。」という意味として対応付けてみます。これらのスピンを今回はx_A,Uのようにスタッフ名とデスク名を添えたスピンで表現することとしましょう。例えばx_B,Xであれば「+1であればスタッフBがデスクXに割り当てられた、−1であれば割り当てられなかった。」という意味で解釈することになります。このように用意した36個のスピンについて前提1と前提2の表現を考えます。
前提1を先ほどのスピンに関する表現としてみましょう。前提1は「スタッフ1人につきデスクは1つ」という内容でした。すなわち「各スタッフについて6つのデスクのうち1つだけが割り当てられる」かつ「各デスクについて6人のスタッフのうち1人だけが割り当てられる」ということです。このうち「スタッフAについて6つのデスクのうち1つだけが割り当てられる」を考えてみると、（∑_{desk∈｛U,V,W,X,Y,Z｝}^x_A,desk+4）²のような二次多項式で表現することが可能です。この式はx_A,U〜x_A,Zのうち1つだけが+1、残りの5つが−1となったときに最小となる式であり、まさに1つのデスクだけが割り当てられることが式の値が最小となることに対応します。他のスタッフ、デスクについても同様の二次多項式で割当てを1つとすることで表現が可能です。
前提2についても考えていきましょう。前提2は「同チームのスタッフが隣接するごとに1点加点」というものでした。例としてスタッフAとBのチームを考えましょう。スタッフAとBはデスクUとXに割り当てられれば1点加点です。これを二次多項式で表現すると（x_A,U+1）（x_B,X+1）/4となります。実際にx_A,Uとx_B,Xに±1を代入してみると、両方とも+1のときのみこの二次多項式は+1となり、他のときは0となります。このままでは逆のデスク割り当てや他のスタッフ、隣接デスクの組み合わせで加点されなくなってしまいますので、すべての組み合わせについてこの式を足し合わせることで、加点される点数を二次多項式で表現することができます。ここで注意するべきは、イジングマシンがイジングモデルを最小とする解を導出するという点です。つまり、隣接による加点が大きいほど、イジングモデルの取る値が小さくなるようにする必要があるため、この二次多項式は正負を反転させて足し合わせることとなります。
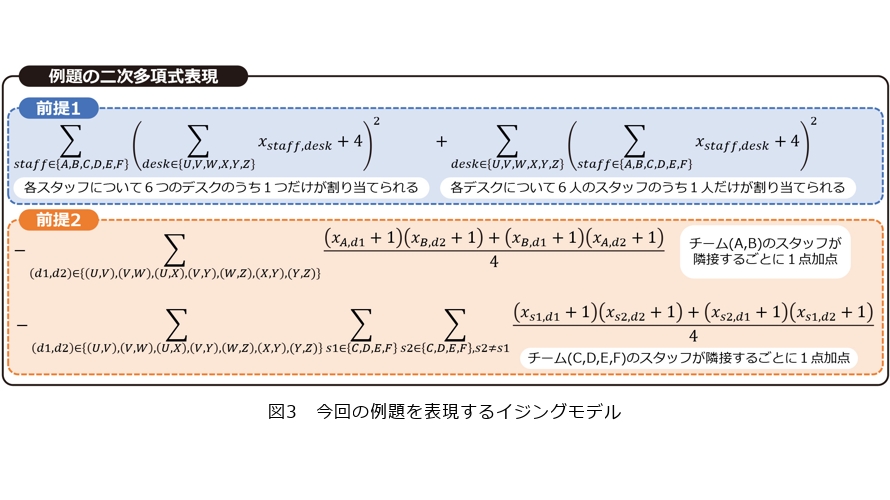
ここまでの内容を踏まえ、考案した多項式を足し合わせると、今回の例題のイジングモデルの全体像は図3のようになります。このようにシンプルな例題であっても、イジングモデルの数式は比較的複雑なものとなります。
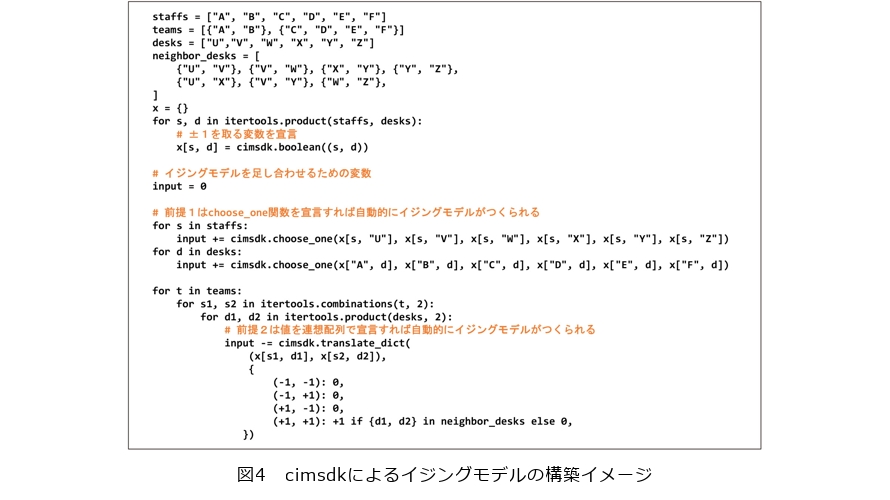
対して、cimsdkによる機能を用いた場合のイジングモデルの構築イメージは図4のようになります。図3の数式を考案する際に必要となった、各多項式がどのようなときにどんな値をとるのか、という点を全く考慮せずにイジングモデルを生成できることが分かります。
実用上の問題を考える場合には、より複雑な前提条件をより多くのスピンに対して考えることとなり、イジングモデルの考案作業はとても煩雑なものとなります。実用問題であれば整数を扱うこともあり、複数の±1を取るスピンを組み合わせて1つの整数として扱う必要も生じます。また、同時に3つ以上のスピンに関するような条件を表現しようとすると三次以上の多項式を扱わなければなりませんが、イジングモデルでは二次多項式しか扱えないので、うまく次数を削減するような取り組みも必要となります。
cimsdkでは、このような複雑になりやすいイジングモデル考案の作業について、整数をはじめとした各種スピンとそれらに関する条件を自動的にイジングモデル変換する機能を提供しています。本技術によりイジングモデルおよびイジングマシンに関する専門知識を持たない人でも、容易にイジングマシンによる高速な求解という恩恵を得られるようになります。特にcimsdkでは他社類似技術に比べて、複数の条件を無制限に再帰的に組み合わせることが可能であり、数学的に定義可能な論理構造をそのまま表現可能である点、任意の連想配列から対応するイジングモデルを自動生成できる点が独自の強みとなっています。今後は自動変換の対象となるスピンと条件を拡充していくことにより、対応可能な実用問題を広げていきます。

イジングマシンを使いこなすうえでのもう1つの課題は、「イジングモデル基底状態探索問題を解くことに特化したコンピュータ」という特性から、それ単体ではアプリケーションを完結させることが難しいという点です。前述したSDKを利用したデータの前処理・後処理や、古典コンピュータが有利な演算などを組み合わせるために、多種演算装置を組み合わせたヘテロジニアスなシステムが必要です。さらに、イジングマシンはPCや一般的なサーバなどと比べるとコストや設置場所の問題があり、多数のマシンを用意することは困難です。そのため、スーパーコンピュータと同様に、複数人で少数のイジングマシンを共用する手段が必要になります。そこでNTTコンピュータ＆データサイエンス研究所では、LASOLV^®などのイジングマシンを効率良く利用するプラットフォームとしてLCS（LASOLV^® Computing System）の開発に取り組んでいます^（4）。前述したSDK等、アプリケーション開発を容易にする開発環境に加え、ユーザのジョブを制御し、CPU等で計算を行うノードやイジングマシンで計算を行うノードを効率良く連携利用しつつ、複数ユーザのジョブが重複しないようにスケジューリングする機能を有しています。
このLCS上で、cimsdkを用いた開発を行うことで、LASOLV^®の実力を活かした応用開拓にも取り組んでいます。例を挙げますと、三菱重工業株式会社との共同実証において、人員リソース計画にイジングマシンを用いる取り組みを実施しました^（5）。同社には、世界中の発電プラント等の点検・補修工事を行うという業務があります。これに対し、さまざまな点検項目に合わせたスキルを有する作業員を派遣する必要がありますが、その人数、連続勤務日数、残業時間など複雑なパラメータも考慮した人員計画を立案しなければなりません。従来は、点検対象プラント数26カ所、作業員141人、日数64日間の期間で、保有スキルなどのさまざまな制約条件を満たす人員計画の解候補を、熟練者が人手で1カ月程度かけて計画を策定していました。これは組み合わせ総数3.48×10¹³³²⁹通りという途方もない規模になりますが、ここに5万スピンを一気に計算できる最新版のLASOLV^®を用いることで、非常に短期間で得られることを実証しました。その高速性を用いて、複数パターンの人員計画策定や、感染症対策等で必要になる計画の随時見直しなどが可能になると期待されています。

本稿では、イジングマシンの特性を踏まえつつ、アプリケーション開発を容易にするSDKの取り組みや、コンピューティングシステム開発の取り組みについて紹介しました。今後、イジングマシンに加え、量子コンピュータの実用化が進む中、その特性を踏まえたSDK等ライブラリの重要性、よりヘテロジニアス性の増したコンピューティングシステムの必要性が増していきます。NTTコンピュータ＆データサイエンス研究所では、量子コンピュータなどの先端的な技術を生かすコンピューティングシステムアーキテクチャのあるべき姿を定義し、研究を発展させていきます。

■参考文献
（1）　https://www.dwavesys.com/solutions-and-products/systems/
（2）　https://www.fujitsu.com/jp/digitalannealer/
（3）　武居・稲垣・稲葉・本庄：“複雑な組合せ最適化問題を解く量子ニューラルネットワーク,” NTT技術ジャーナル, Vol. 29，No. 5，pp. 11-14, 2017.
（4）　新井・八木・内山・富田・宮原・巴, 堀川：“イジング型計算機による組合せ最適化のためのハイブリッド計算基盤,” NTT技術ジャーナル, Vol. 31，No. 11，pp. 27-31, 2019.
（5）　https://group.ntt/jp/newsrelease/2022/04/25/220425a.html