現代社会は道路、通信、電力などのインフラによって支えられています。このようなインフラはどのような構造になっているでしょうか。例えば、高速道路は日本全国を網羅的にカバーしています。また、通信の基幹網でもケーブルを張り巡らせて全国をカバーしています。このように、現代のインフラは道路やケーブルなどの部品が集まってネットワーク構造をなしています。
このようなインフラが現代社会の基盤となるためには、さまざまな要件があります。例えば道路網においてはなるべく渋滞しないこと、通信網においては通信がなるべく遅延しないことや、通信障害がなるべく起こらないことが求められます。それに対応して、インフラの良さに関する定量化・数値化された指標が考えられます。例えば道路網や通信網では混雑、すなわち渋滞や遅延が少ないほど良いとか、通信網では部品故障に対する耐性が高いほど良いといった指標が考えられます。現代社会の基盤となる「良い」、すなわち高性能・高信頼なインフラを実現するためには、先に挙げたような指標の解析を行う手法を開発することが重要です。そのような解析として、例えばネットワークのどの部分が混雑するか解析する混雑解析、ネットワークがどのくらい故障や災害に強いかを解析する信頼性解析、またどの部品を補強すべきか解析する脆弱性解析などが挙げられます。
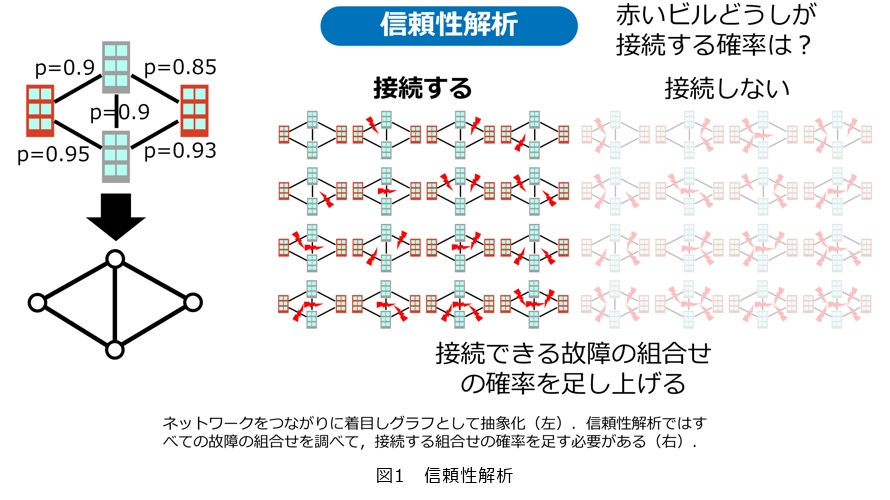
では、ネットワークインフラの解析はどのように行えばよいでしょうか。解析を行う際に、道路やケーブルなどの各部品を物理的な装置として扱うと計算機にとって扱いづらいため、ネットワークのつながりに着目して抽象化することを考えます（図1左）。ここで各部品はノードどうしを結ぶ線（辺）に対応します。これは数学的にはグラフ理論におけるグラフを考えることにあたります。この抽象化したグラフを扱える解析法をつくることにより、ネットワークの本質的な構造に着目した解析を行います。
しかし、たとえ抽象化したとしても、ネットワーク解析は計算機で解くのが難しい問題になっています。それは、ネットワークインフラは複数の部品から構成されていて、その部品の組合せの数が部品の個数に対して指数的に多いためです。N個の部品があればそのネットワークの状態の組合せの数は2のN乗、すなわち2をN回かけた数になります。例えばたった50個の部品から構成されるネットワークでも部品の組合せは2の50乗で約1000兆通りに及びます。
そして、実際にそのような膨大な数の組合せを調べたり数え上げたりしなければならないネットワーク解析が数多くあります。例えば、信頼性解析では、特定のノード（図1においてはビル）どうしがケーブルを介して接続できる確率を解析することになります。このとき、一部の部品が故障していてもビルどうしは相変わらず接続できることもあります。したがって、各部品について故障している・していないの2通りの可能性を考え、それらの組合せをすべて調べて、接続できる故障の組合せの確率を足し上げる必要があります（図1右）。同様に、混雑解析ではどの道路やケーブルなどが混雑するかを解析しますが、この際あり得る経路をすべて調べ上げる必要があります。1つひとつの経路も部品の組合せであり、やはり膨大な数存在するため、計算機でも計算が困難な問題になります。

では、膨大な数の組合せに対処するにはどうすればよいのでしょうか？　従来は、膨大な数の組合せのうち一部のみを調べたり数えたりすることでこの問題に対処してきました。これにより、調べたり数えたりする組合せを大幅に削減し、計算時間が増大してしまう問題を解決しています。しかし、このアプローチでは一部の組合せしか調べていないため、解析が不正確になってしまうという欠点がありました。インフラは多くの人が用いるものであり、社会的に大事なので、多少時間がかかっても精緻な解析が要求される場面があります。
そこで、本稿では圧縮計算というコンセプトを考えます。これは、調べたい組合せを圧縮して保持し、圧縮したまま解析、すなわち計算に用いるという考え方です。もしこれが実現できれば、すべての組合せを調べられるので精緻な解析ができ、また計算時間が圧縮後の大きさに比例するため計算の高速化を望めます。
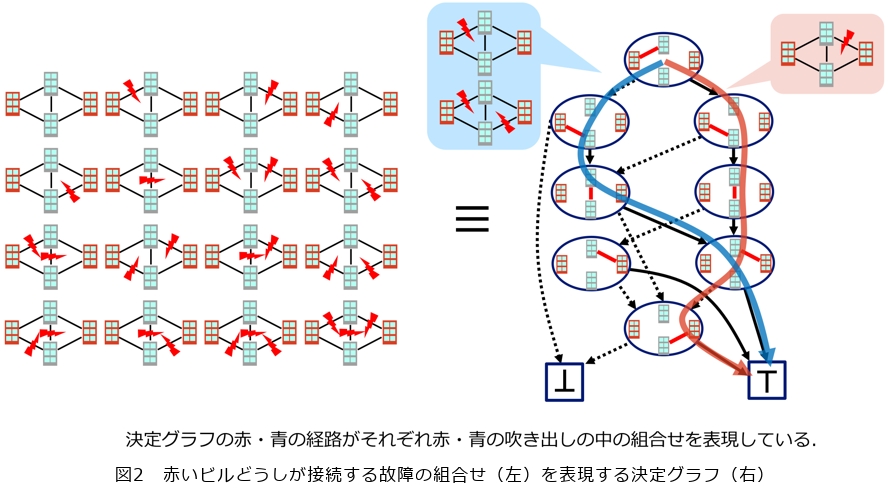
これを実現する手法の1つが、決定グラフ＊と呼ばれる表現方法です。決定グラフは図2右のように節点を矢印で結んだ図で組合せを表現し、上から下までたどるとすべての組合せが得られます。このとき、実線矢印をたどると部品が動作していること、点線矢印をたどると部品が故障していることを表します（図2）。より一般には表現する組合せについてのその部品の有無を表します。決定グラフでは、組合せのうち共通な部分をまとめることで小さな表現を達成しています。例えば、信頼性解析において100ノード規模のネットワークになると、ビルどうしが接続する故障の組合せが10の41乗個に及ぶこともありますが、決定グラフではわずか3000節点程度で表現できる、という場合があるなど驚異的な圧縮を実現できます。
さらに、決定グラフでは圧縮したままで組合せに関する最適化や数え上げなどの計算ができます。例えば、特定の条件（ある部品が故障しているなど）を満たす、赤いビルどうしが通信できる故障の組合せの個数は、図2の決定グラフがあれば組合せをすべて調べ上げることなく計算できます。この計算は圧縮後の節点数に比例する時間で行えます。つまり、決定グラフは圧縮計算を実現する道具として使えます。これらの性質から、決定グラフはこれまでも信頼性解析などのさまざまなネットワーク解析問題を解くために用いられてきました。
NTTコミュニケーション科学基礎研究所では、決定グラフを用いた圧縮計算における圧縮計算できる計算の種類や、圧縮の方法を拡張することによって、より高度な解析を精緻に行えるアルゴリズムを開発してきました。以後、本稿では計算の拡張および圧縮の拡張によってそれぞれできるようになったネットワークインフラ解析アルゴリズムについて紹介します。

＊　決定グラフ：二分決定グラフ（BDD: Binary Decision Diagram）や、その亜種であるゼロサプレス型二分決定グラフ（ZDD: Zero-suppressed BDD）などを指します。いずれも組合せをグラフ理論的なグラフとして表現するデータ構造。

道路インフラや通信インフラにおいて、その多くの利用者の経路（道路においては道順、通信においてはデータが伝送される経路）が重なってしまうと、その部分で混雑が発生して移動時間が長くなってしまいます。そこで、インフラの運営者は道路の道幅や通信ケーブルの帯域などを補強することで混雑を解消し、全利用者の平均移動時間を短くしたいと考えます。しかし、インフラのユーザは一般には利己的に振る舞うことを仮定して補強を考えなければなりません。例えば、すべての車が幹線道路に集中すると渋滞が起こってしまいますが、それでも迂回路よりも早く移動できるならばそれぞれの車は迂回路ではなく幹線道路を利用すると考えられます。
このような状況でどのようにインフラを補強すればよいでしょうか？　実は、むやみに道幅を増やすなどの補強を行うと、そこにさらに多くの交通が集中し、かえって平均移動時間が長くなってしまうこともあります。これを交通工学の分野でブライスのパラドックスと呼びます。これには均衡状態と呼ばれる状態が関係してきます。ユーザが利己的にインフラを利用していると、もし今通っている経路より移動時間が短い経路があればユーザはそちらに切り替えることになります。各ユーザがそのような動きを繰り返すと、最終的に全ユーザが同じ移動時間で、かつその時点で移動時間がもっとも短い経路を各々選ぶ状態になります。これを均衡状態と呼びます。平均移動時間を短くするためには均衡状態における混雑を緩和することが重要ですが、安易にインフラの補強を行うと均衡状態が変化してしまうのがブライスのパラドックスの原因です。
したがって、ユーザの移動時間を短くする補強の方法を求めるためにはまず均衡状態を求められなければなりません。ここで、均衡状態では全ユーザが同じ移動時間となってはいますが、全ユーザが同じ経路を使っているとは限りません。このため、均衡状態は膨大な数の経路の組合せ、すなわち組合せの組合せとなります。したがって、たとえ圧縮を用いても均衡状態を求めること自体が困難な問題でした。また、そこから均衡状態の移動時間が短くなるインフラの補強の仕方を探すのもまた困難な問題でした。
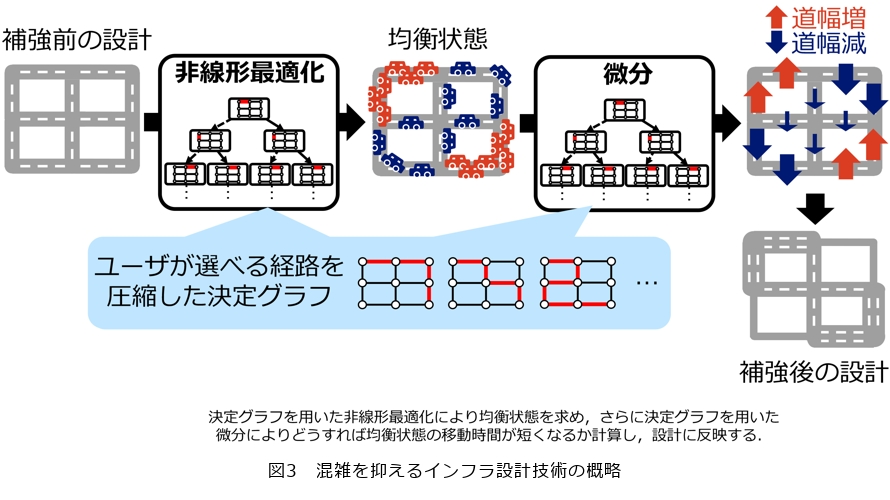
そこで私たちは、ユーザが選べるすべての経路を決定グラフへと圧縮し、圧縮計算を用いることで、均衡状態の移動時間が短くなるような補強の仕方を発見するアルゴリズムを開発しました（図3）。
本稿では技術について簡単に紹介します。まず、均衡状態の計算は組合せの組合せを求める問題になるので困難な問題でしたが、私たちはこれが組合せ的な制約のもとでの非線形最適化問題を解くことで求められることに着目しました。この最適化問題を解くためには従来選べる経路を1つひとつ調べる必要がありましたが、決定グラフを用いた圧縮計算により非線形最適化を解く方法を考案したことで、均衡状態を現実的な時間で求められるようになりました^（1）（図3左）。次に、道幅を少し変化させたときの微分、すなわち均衡状態やそのときの移動時間がどう変化するかも圧縮計算によって求められる方法を考案しました。これによって、インフラのどの部品を補強すれば平均移動時間が短くなるかが分かるようになりました^（2）（図3右）。これらの圧縮計算により、現実的な時間内に計算できるアルゴリズムを開発できました。
提案手法により、経路の個数に比例していた計算時間が決定グラフの大きさに比例して終わるようになりました。例えば、多点間通信の設定では、10の28乗個の経路をわずか1万節点程度の決定グラフで表現することで、10の25乗倍という劇的な高速化を実現しています。この技術を用いたネットワークインフラ設計を通じて、道路における渋滞や通信における遅延などさまざまな混雑問題にアプローチできると考えています。

インフラは物理的な設備を使っている以上、どうしてもケーブルなどの各部品が故障してしまうことがあります。したがってインフラでは、平常時の性能が高いことに加えて、故障耐性も高いことが求められます。故障耐性を測るために、従来は図1にあるような信頼性解析、すなわちノードどうしが接続する確率の計算が行われており、決定グラフを用いた圧縮計算により200ノード程度の現実的なネットワークで精緻な誤差なしの解析が行えました。
しかし、障害が起こった際にはその障害の規模も大切な指標となります。多数のユーザに影響が及ぶ大規模障害は、小規模障害と比べると特に起こってほしくないものですが、従来の信頼性解析では障害規模の考慮ができていませんでした。そこで、小規模障害と大規模障害で別々にその発生確率を解析する、すなわち、障害規模別にその発生確率を解析するのがここで行いたいことです。
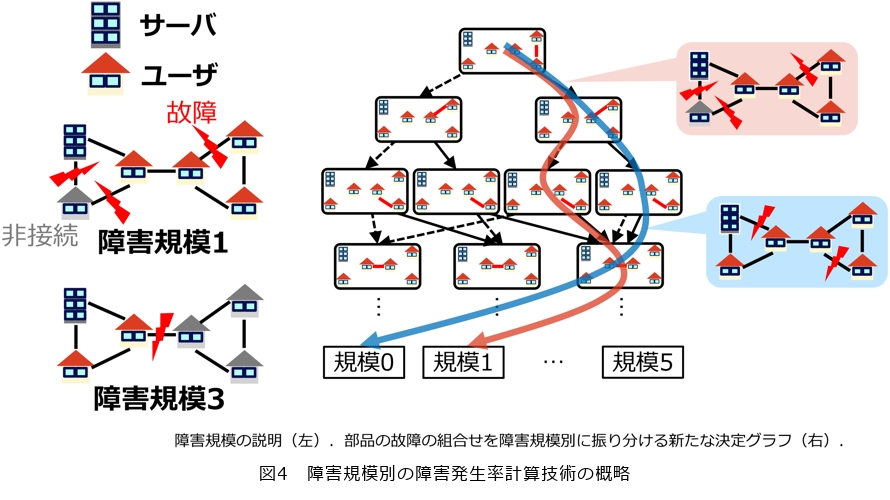
この問題においては、ネットワークのノードがサーバとユーザの2種類あり、サーバに接続できないユーザの数を故障規模とします（図4左）。このとき、起きた故障の数と障害規模は必ずしも連動していないことが特徴で、上の例では故障は3カ所で起こっているのに対し非接続になったユーザは1軒だけですが、下の例では故障1カ所に対し3軒の非接続ユーザが発生しています。この状況下での障害規模別の障害発生率の誤差なしの計算を行うことを考えます。これにより、インフラ運用者は障害規模別に発生確率に関する設計基準を決めて、設計したネットワークが基準を満たすか確認することができるようになります。
しかし、規模別に障害発生率を計算することはとても困難な問題です。それは各部品の故障の組合せが膨大な数あることに加えて、どのユーザが障害を受けているかに関する組合せも考える必要があったためです。従来の信頼性の圧縮計算では、どのユーザが障害を受けているかを決め打ちすれば、そのような障害が起こる確率を計算することができました。この計算を障害を受けるユーザに関するすべての組合せで行えば規模別の発生率が計算できますが、たった50ユーザでも1000兆回の圧縮計算を繰り返すことになり現実的な方法ではありませんでした。
そこで私たちは、従来の障害が起こっているか起こっていないか振り分ける決定グラフに代わって、部品の故障の組合せを障害規模別に振り分ける新しい決定グラフを開発しました^（3）（図4右）。これにより、一度の圧縮計算によってすべての障害規模の確率を計算することができるようになり、従来の圧縮計算を用いた方法と比べても大幅な高速化を実現しました。例えば、各都道府県に1つずつノードがあるような50ノード程度のネットワークでは、1秒以内に規模別の障害発生率を計算できるようになり、従来と比べて10万倍以上高速になりました。さらに、この2倍の100ノード規模では、問題としては2の50乗で1000兆倍問題が難しくなりますが、それでも数10分から1時間強という現実的な時間での計算を可能にしています。
提案手法によって、現実的な規模のネットワークでも障害規模別の設計基準を満たしているかを厳密に確認できるようになったため、現代や将来のネットワークの高信頼設計に貢献したいと考えています。今後は本技術をさらに発展させて、大規模障害が起こりづらいネットワークを自動的に設計できる技術を開発したいと考えています。

ここまで、決定グラフを用いた圧縮計算を用いたネットワーク解析アルゴリズムの実例について述べてきました。決定グラフでできる圧縮計算の種類を増やすことにより混雑を抑えるインフラ設計技術ができ、また新たな圧縮の方法、すなわち新たな決定グラフの考案によって障害規模別の障害発生率計算技術ができました。私たちはこれ以外にも、ネットワーク信頼性の分散値の計算^（4）や、部品に故障が起こる状況下でサーバに接続できるユーザの数の期待値の計算^（5）などを高速に行うアルゴリズムを、決定グラフを用いた圧縮計算を拡張することにより提案しています。今後も、決定グラフを用いた圧縮計算によって、ネットワーク解析に限らず組合せを扱う必要がある問題の高速なアルゴリズムを開発します。
私たちの技術は基礎研究の段階であり、インターネット上で公開されている現実的なネットワーク形状を用いた実験はできているものの、実際に現在運用・設計されているネットワークの解析は未着手です。そこで、運用・設計されているネットワークのリアルなデータを用いて提案したアルゴリズムによる解析を行い、知見を得ることが次の段階と考えています。

■参考文献
（1）　K. Nakamura, S. Sakaue, and N. Yasuda:“Practical Frank-Wolfe method with decision diagrams for computing Wardrop equilibrium of combinatorial congestion games,”Proc. of AAAI 2020, pp. 2200-2209, 2020.
（2）　S. Sakaue and K. Nakamura:“Differentiable equilibrium computation with decision diagrams for Stackelberg models of combinatorial congestion games,”Proc. of NeurIPS 2021, pp. 9416-9428, 2021.
（3）　K. Nakamura, T. Inoue, M. Nishino, N. Yasuda, and S. Minato:“Exact and efficient network reliability evaluation per outage scale,”Proc. of ICC 2023, pp. 4564-4570, 2023.
（4）　K. Nakamura, T. Inoue, M. Nishino, and N. Yasuda:“Impact of link availability uncertainty on network reliability: analyses with variances,”Proc. of ICC 2022, pp. 2713-2719, 2022.
（5）　K. Nakamura, T. Inoue, M. Nishino, N. Yasuda, and S. Minato:“A fast and exact evaluation algorithm for the expected number of connected nodes: an enhanced network reliability measure,”Proc. of INFOCOM 2023, pp. 1-10, 2023.