2024年9月号
特集1
たくさんのデータの中から素早く知識を発見―─計算の枝刈りによる高速化手法を活用した厳密性を担保した大規模データ解析
- 大規模データ
- データ解析
- 高速化
現在、AI(人工知能)を活用した効果的なデータ解析に対する関心が高まっています。しかし膨大なデータの解析には多大な計算コストが必要です。一般的に計算コストを低減するために近似的な処理が行われますが、近似処理では正確な解析結果を得ることが難しいという問題があります。本稿では計算の枝刈りを行うことにより高速性と厳密性を両立させたデータ解析手法の代表的な例を紹介します。
藤原 靖宏(ふじわら やすひろ)
NTTコミュニケーション科学基礎研究所
大規模データに対するデータ解析
近年、データサイエンスに対する関心が急速に高まっています。2012年にハーバード・ビジネス・レビューがデータサイエンティストを「21世紀でもっともセクシーな職業」として紹介したことがその1つの象徴ですが、現在では多くの企業がデータサイエンスを積極的に活用し、多くの大学がデータサイエンスを支える人材の育成に力を入れています。このトレンドは年々強まっており、データサイエンスの重要性はますます増大しています。データサイエンスへの関心が高まる理由の1つとして、企業がデータ解析を通じて効果的なマーケティング戦略を立てるなどにより、ビジネス価値を向上させることが挙げられます。エコノミスト誌が、データが持つ価値に注目し、「データは新しい石油である」という記事を発表したこともあり、データ解析の重要性が広く認識されています。
データ解析の対象であるデジタルデータの量は急激に増加しており、市場調査会社の報告によると、2014年の約12.5ゼタバイト(約125億テラバイト)であったデジタルデータの量は2024年には約147ゼタバイト(約1470億テラバイト)に達すると予測されています。このような膨大なデータの中からパターンやトレンドを発見し、人間の意思決定を支援するデータ解析は今後データという新しい資源を有効に活用していくために不可欠な技術です。しかし膨大なデータに対してデータ解析を行うには莫大な計算リソースが必要になり、その結果、データ解析の計算コストの増大という大きな課題が生まれます。
計算コストを低減するために一般的には近似計算が行われます。しかし近似計算は高速性を得る代わりに精度を犠牲にするため、計算時間を短くすると解析結果の精度が低下し、一方で精度を向上させるためには計算時間が増加するというトレードオフが生じます。データ解析は人間の意思決定のサポートに用いられることが多いため、解析結果の厳密性を犠牲にするアプローチは好ましくありません。
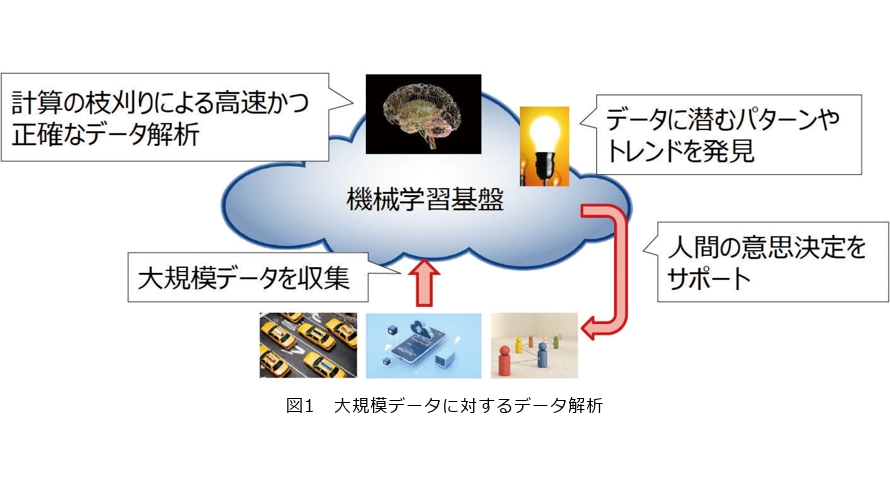
そこで私たちは高速性と厳密性を両立させたデータ解析のための機械学習基盤の構築に向けて研究開発を進めています(図1)。この機械学習基盤において高速性と厳密性を確保する鍵となるのが計算の枝刈り手法です。計算の枝刈り手法は計算結果の厳密性を損なわない範囲で不要な計算を省くことで高速化を実現します。本稿ではその代表的なものとして①上限値・下限値による計算の省略、②解になり得ない計算の打ち切り、③楽観的処理による高速計算を紹介します。
上限値・下限値による計算の省略
はじめに上限値・下限値を用いた計算省略による枝刈り手法を紹介します(1)。この手法はスコアを厳密に計算した結果、行う必要がないことが分かる処理をスコアの上限値と下限値を用いて高速に特定することで不要な計算を省きます。この手法の例としてCUR分解の高速化の研究があります。
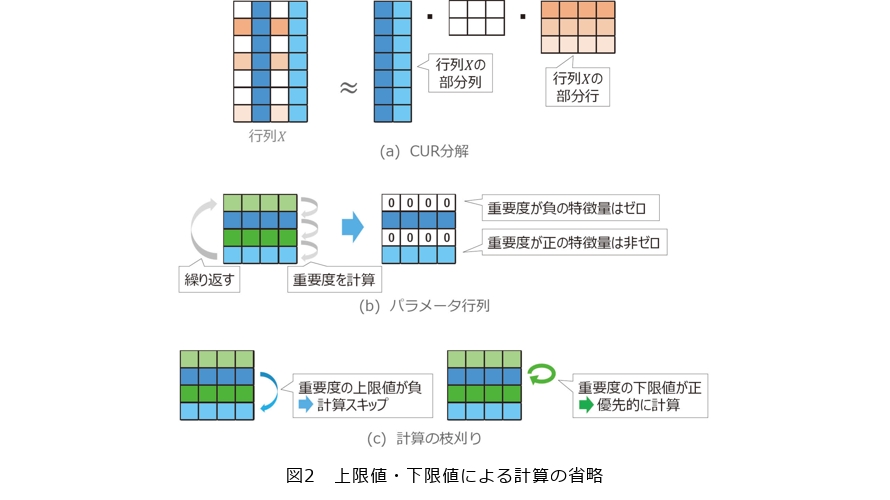
CUR分解は与えられた行列 X をその部分列と部分行を用いて分解する技術です(図2(a))。例えば図2(a)の例では行列 X の大きさは7×4ですが、CUR分解ではこの行列 X を青色の2つの部分列とオレンジ色の3つの部分行を用いて表現します。CUR分解は与えられた行列をよく表現する特徴的な部分列と部分行を求めることで高次元データから重要な特徴量を抽出することができます。例えば工場における高機能のセンサから長期間発生する時系列データをセンサ数×時間長の行列で表すと行と列の数は非常に大きくなりますが、CUR分解を適用することで行列をよく表現する部分行と部分列を取り出すことができ、非常に大きいデータの中から特徴的なセンサと時間帯を特定することができます。特徴的な個所を特定することで工場の生産性に関する効果的な要因分析などが可能になります。
CUR分解では重要な特徴量を特定するために行列 X における各特徴量に対応するパラメータ行列を導入し特徴量ごとの重要度を計算します。そして重要度が負の特徴量を0とすることで重要な特徴量を抽出します。例えば図2(b)におけるパラメータ行列の行数は4ですが、このパラメータ行列の各行は図2(a)の行列 X の各列の特徴量に対応しています。図2(b)のパラメータ行列では1行目と3行目が0になっていますが、これは図2(a)の行列 X の1列目と3列目の特徴量が重要でない一方、2列目と4列目の特徴量が重要であることを表しています。このようにCUR分解ではパラメータ行列から重要な特徴量を抽出しますが、この抽出のために繰り返し計算を収束するまで行う必要があるため、計算コストも高くなり、大規模データに適用するのは難しいという問題がありました。
そこで私たちは重要度の上限値と下限値を用いて重要度の繰り返し計算を軽量化することで高速にCUR分解を行う手法を提案しました(1)。具体的には図2(c)のように重要度の上限値が負であれば厳密な重要度も負になるためその特徴量の計算をスキップします。また重要度の下限値が正であれば厳密な重要度も正になるため、その特徴量の計算を優先して行います。結果的に重要度の上限値と下限値を用いることで不要な計算を省略し、重要度が正となる特徴量を集中的に計算することが可能になり、CUR分解の高速化が実現しました。
解になり得ない計算の打ち切り
次に解になり得ない計算を打ち切ることで高速化を行う手法について紹介します(2)。この手法は探索処理の過程で解になり得ないパターンを保持し、そのパターンが再び探索処理に現れたときに処理を打ち切ることで高速化を実現します。部分グラフ検索の高速化技術がその一例です。
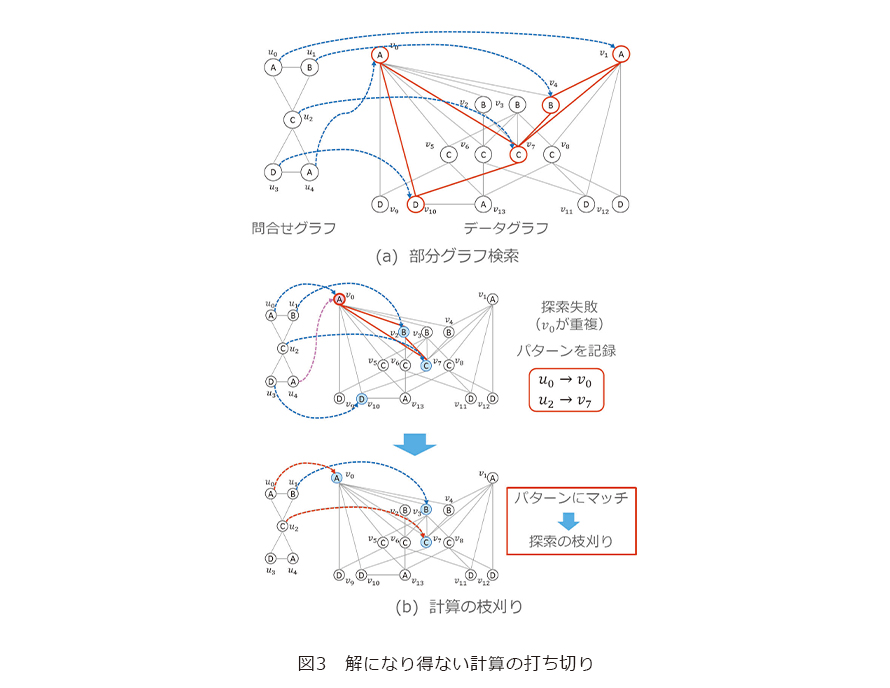
部分グラフ検索はノードにラベルの付いた大規模なデータグラフの中から問合せグラフと同じ構造を持つ部分グラフを探索する処理です。例えば図3(a)の例における問合せグラフはラベルがA、B、Cからなる三角形とラベルがC、D、Aからなる三角形から構成されていますが、データグラフにおけるそのマッピング先の赤い部分グラフも同様にラベルがA、B、Cからなる三角形とラベルがC、D、Aからなる三角形から構成されています。部分グラフ検索のアプリケーションの一例として有機化合物の検索があります。有機化合物の分子間の結合関係はグラフで表現することができ、また共通の結合関係を持つ化合物は似た性質を持つことが知られています。そのため、部分グラフ検索を利用して同じ結合関係を持つ有機化合物を見つけることで、問合せと類似した性質を持つ有機化合物を発見することが可能となります。しかし部分グラフ検索は問合せグラフのノード1つひとつをデータグラフにマッピングする必要があるため、その最悪時間計算量はグラフのサイズに対して指数関数になります。そのため部分グラフ検索はデータグラフが大規模になると膨大な処理時間が必要になるという問題があります。
そこで私たちはノード1つひとつのマッピングが失敗したパターンを保持し、マッピングにおいて失敗したパターンが再度現れた場合に処理を早期に終了する手法を提案しました(2)。例えば図3(b)上の場合、問合せグラフのラベルがAの ![]() をデータグラフの
をデータグラフの ![]() に、ラベルがBの
に、ラベルがBの ![]() を
を ![]() に、ラベルがCの
に、ラベルがCの ![]() を
を ![]() に、ラベルがDの
に、ラベルがDの ![]() を
を ![]() にマッピングすると、ラベルがAであるノード
にマッピングすると、ラベルがAであるノード ![]() は
は ![]() にマッピングせざるを得なく探索が失敗します。この探索の失敗について調べてみると
にマッピングせざるを得なく探索が失敗します。この探索の失敗について調べてみると ![]() を
を ![]() に
に ![]() を
を ![]() にマッピングすることが原因であることが分かります。これはラベルがCの
にマッピングすることが原因であることが分かります。これはラベルがCの ![]() を
を ![]() にマッピングすると
にマッピングすると ![]() につながったラベルがDのノードは
につながったラベルがDのノードは ![]() しかないため
しかないため ![]() を
を ![]() にマッピングせざるを得なく、さらに、
にマッピングせざるを得なく、さらに、![]() と
と ![]() につながっているラベルがAのノードは
につながっているラベルがAのノードは ![]() しかないため、もし
しかないため、もし ![]() を
を ![]() にマッピングしてしまっていると探索が失敗するからです。そのため探索が失敗する原因となった
にマッピングしてしまっていると探索が失敗するからです。そのため探索が失敗する原因となった ![]() を
を ![]() に
に ![]() を
を ![]() にマッピングするパターンを打ち切り条件として保持します。そして再度検索の過程でこのパターンが現れた時点で探索処理を打ち切ります。例えば図3(b)下では、
にマッピングするパターンを打ち切り条件として保持します。そして再度検索の過程でこのパターンが現れた時点で探索処理を打ち切ります。例えば図3(b)下では、![]() を
を ![]() に、
に、![]() を
を ![]() に、
に、![]() を
を ![]() にマッピングしていますが、このマッピングは保持していた打ち切り条件に一致するため、探索を進めることなく処理を中断します。このように、解になり得ない計算を打ち切ることで不必要な処理を枝刈りし、部分グラフ検索を高速に行うことが可能になります。
にマッピングしていますが、このマッピングは保持していた打ち切り条件に一致するため、探索を進めることなく処理を中断します。このように、解になり得ない計算を打ち切ることで不必要な処理を枝刈りし、部分グラフ検索を高速に行うことが可能になります。
楽観的処理による高速計算
最後に楽観的な処理を行うことで計算を枝刈りする手法を紹介します(3)。この手法は制約条件を一時的に外して高速に解を求めた後に、得られた解が制約条件を満たすかを確認することで高速化を実現します。この手法の例としてb-Matchingグラフの高速計算があります。
b-Matchingグラフは、各データがちょうど決められた数の近傍データとつながっている近傍グラフです。近傍グラフとしてはデータごとに k 個の近傍データをつなげる k -近傍グラフがよく用いられますが、k -近傍グラフではデータごとに k 個の近傍データにつなげた結果、エッジの数が k 個より多くなるデータが発生することがあります。例えば、図4(a)左の例は各データから2個の近傍データをつなげる場合の k -近傍グラフの例ですが、2個の近傍データをつなげた結果、![]()
![]() 、
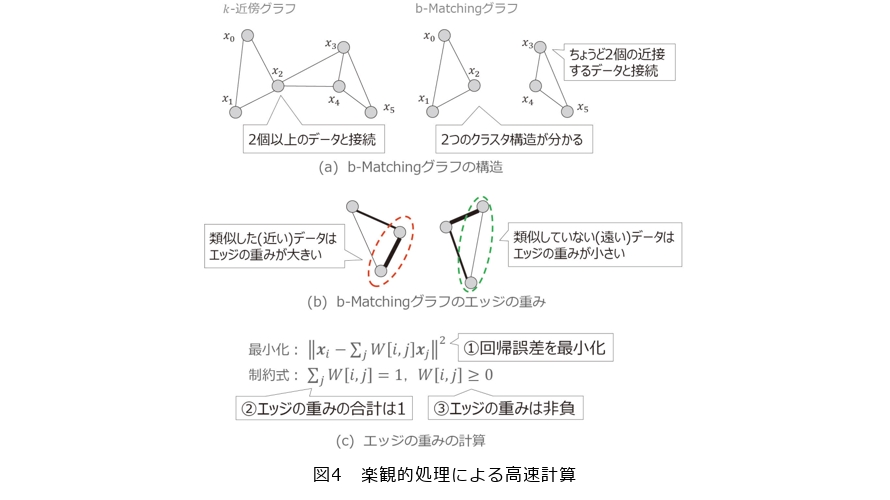
、![]() のように2個より多い数の近傍データにつながるデータが発生しています。一方、図4(a)右の例はデータごとに2個の近傍データとつなげるb-Matchingグラフですが、b-Matchingグラフでは各データのエッジの数がちょうど2になっています。k -近傍グラフでは多くの近傍データとつながるデータが発生するため、すべてのデータが1つのクラスタとなっていますが、b-Matchingグラフでは図4(a)右のようにエッジの数が多くなるデータが発生していないため、データが持つ2つのクラスタを抽出することができます。このようにb-Matchingグラフはエッジの数が多くなるデータが発生しないため、データが持つクラスタ構造をとらえやすいという利点があります。またb-Matchingグラフにおけるエッジの重みはデータ間の類似度によって決まります。具体的には図4(b)のように、b-Matchingグラフではデータどうしが近い距離にある類似したデータ間のエッジの重みは大きくなり、データどうしが遠い距離にある類似していないデータ間のエッジの重みは小さくなります。結果としてb-Matchingグラフはクラスタ構造をとらえやすく、類似したデータのエッジの重みは大きくなるため、同じクラスタで距離が近いデータほどよくつながるという特徴があります。同じクラスタで距離が近いデータは同じラベルを持つ傾向があるため、データのラベルをその近傍データから効果的に推定することができ、駐車場の状況推定やクレジットカード詐欺の検出などに応用することができます。
のように2個より多い数の近傍データにつながるデータが発生しています。一方、図4(a)右の例はデータごとに2個の近傍データとつなげるb-Matchingグラフですが、b-Matchingグラフでは各データのエッジの数がちょうど2になっています。k -近傍グラフでは多くの近傍データとつながるデータが発生するため、すべてのデータが1つのクラスタとなっていますが、b-Matchingグラフでは図4(a)右のようにエッジの数が多くなるデータが発生していないため、データが持つ2つのクラスタを抽出することができます。このようにb-Matchingグラフはエッジの数が多くなるデータが発生しないため、データが持つクラスタ構造をとらえやすいという利点があります。またb-Matchingグラフにおけるエッジの重みはデータ間の類似度によって決まります。具体的には図4(b)のように、b-Matchingグラフではデータどうしが近い距離にある類似したデータ間のエッジの重みは大きくなり、データどうしが遠い距離にある類似していないデータ間のエッジの重みは小さくなります。結果としてb-Matchingグラフはクラスタ構造をとらえやすく、類似したデータのエッジの重みは大きくなるため、同じクラスタで距離が近いデータほどよくつながるという特徴があります。同じクラスタで距離が近いデータは同じラベルを持つ傾向があるため、データのラベルをその近傍データから効果的に推定することができ、駐車場の状況推定やクレジットカード詐欺の検出などに応用することができます。
b-Matchingグラフを計算するためには、(1)各データにつながっている決められた数の近傍データを求める処理と、(2)各エッジの重みを求める処理を行う必要があります。(1)の処理について本稿では詳細な説明は省略します。(2)のエッジの重みを求める処理では図4(c)に示す最適化問題を解く必要があります。図4(c)の式において ![]() は i 番目のデータ、
は i 番目のデータ、![]() は i 番目と j 番目のデータ間のエッジの重みを表します。この最適化問題では図4(a)に示すとおり、①回帰誤差を最小化するようにエッジの重みを計算しますが、②エッジの重みの合計が1であり、③エッジの重みは非負であるという制約があります。これらの制約が付いた回帰分析を解くには一般的に最適化ソルバを用いる必要があります。しかし最適化ソルバは高い計算コストが必要であるため、b-Matchingグラフにおけるエッジの重みを求める処理時間が長くなるという問題があります。
は i 番目と j 番目のデータ間のエッジの重みを表します。この最適化問題では図4(a)に示すとおり、①回帰誤差を最小化するようにエッジの重みを計算しますが、②エッジの重みの合計が1であり、③エッジの重みは非負であるという制約があります。これらの制約が付いた回帰分析を解くには一般的に最適化ソルバを用いる必要があります。しかし最適化ソルバは高い計算コストが必要であるため、b-Matchingグラフにおけるエッジの重みを求める処理時間が長くなるという問題があります。
そこで私たちは③エッジの重みは非負であるという制約をいったん除外することでエッジの重みを高速に計算する手法を提案しました(3)。この手法は、①回帰誤差の最小化と②エッジの重みの合計が1という制約下で解を求めるために、まずソルバではなく回帰分析を用いてエッジの重みを計算した後に、合計が1になるように正規化します。そして求めたエッジの重みが③の制約を満たしているかを確認します。提案手法はエッジの重みが③の制約を満たしていない場合のみソルバを用いてエッジの重みを計算するため、ソルバを用いる回数を減らすことができ、高速化を実現しています。このように提案手法は制約を一時的に除外しても、結果的にその制約を満たす解が得られるだろうという楽観的な処理を行うことで高速化を達成しています。
今後の展望
データベース技術やインターネット技術の著しい進展に伴い、私たちはこれまでにない規模のデジタルデータを収集・解析することが可能になりました。この結果、データは新たな資源としての重要性を増し、さまざまな分野で新しい価値の発見や意思決定において活用されるようになっています。社会全体がデータを活用する方向へとシフトしており、この動きは今後ますます加速すると考えられます。
私たちの研究チームはこの社会的な動きに対応し、高速性と厳密性を両立した機械学習基盤の実現をめざして日夜研究を進めています。具体的には膨大なデータを迅速かつ正確に処理できるアルゴリズムの開発や効率的なデータ管理システムの構築に取り組んでいます。これにより、より多くの人々がデータを有効に活用できる環境を整えたいと考えています。
将来的には私たちが開発する機械学習基盤が社会のインフラとして広く普及し、さまざまな領域でデータ解析を活用した革新的なアプリケーションが誕生することをめざしています。このような未来を実現するために、私たちは引き続き最先端の技術を追求し、データ解析の可能性を最大限に引き出すことに努めていきます。そしてデータを通じて社会全体の発展に貢献できるよう、努力を惜しまず研究を進めていきます。
■参考文献
(1) Y. Ida, S. Kanai, Y. Fujiwara, T. Iwata, K. Takeuchi, and H. Kashima:“Fast Deterministic CUR Matrix Decomposition with Accuracy Assurance,”ICML 2020,pp. 4594-4603,July 2020.
(2) J. Arai, Y. Fujiwara, and M. Onizuka:“GuP: Fast Subgraph Matching by Guard-based Pruning,”Proc. of ACM Manag. Data, Vol.1,No.2, 167,pp.1-26, 2023.
(3) Y. Fujiwara, A. Kumagai, S. Kanai, Y. Ida, and N. Ueda:“Efficient Algorithm for the b-Matching Graph,”KDD 2020,pp. 187-197,August 2020.

藤原 靖宏







データの重要性が増しさまざまな分野で活用が進んでいます。私たちは高速かつ厳密な機械学習基盤の開発に取り組み、大規模なデータを利用したデータ解析が広く活用される社会の実現をめざして研究を進めていきます。